直射式激光三角法的优化方案

直射式测量光学系统如图2.17所示。激光器发出的光束，经聚光后垂直入射到被测物体表面上产生一光点，光点的一部分散射光通过接收透镜成像于光电检测器的感光面上。如果被测物体沿激光光轴移动或表面高度变化，将导致入射光点沿入射光轴移动，那么光电探测器上的成像点也会相应随之移动，根据物像之间的关系从而确定被测物的变化。

图2.17中，O 平面为被测物的基准位置；P 点为成像光点的基准点；a 为激光光轴与接收透镜光轴的交点到接收透镜主平面的距离，定义为工作距；b 为接收透镜主平面到成像基准点的距离，定义为像距；α 为激光光轴与成像光轴之间的夹角，定义为工作角；β 为光电探测器基线与成像光轴间的夹角，定义为成像角；x 为成像光点相对于成像基准点移动的距离；y 为被测物体相对于基准位置移动的距离。

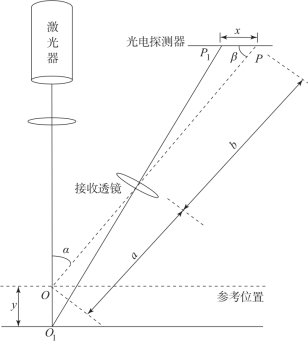
图2.17　直射式激光三角测量示意图

将激光轴线与成像光轴的交点所在的位置作为参考位置，而这时像点的位置就是测量的参考零点。根据图2.18光斑成像示意图，可知要使光斑在探测器上成清晰的实像就要满足近轴透镜成像公式，即要满足式（2.79）：

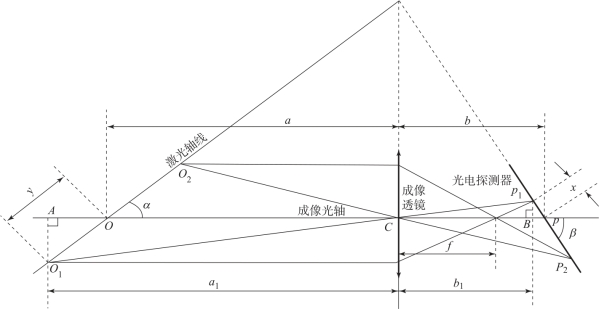
图2.18　轴外目标成像示意图

式中，f 为接收透镜的焦距。

当被测物体沿激光轴线远离激光器时，即光斑由O 点移动到O1，对于透镜光轴以外的光线，要想在光电探测器上成清晰的像也要满足成像公式，即

此时，

由ΔCAO1～ΔCBP1 可以得到

(www.xing528.com)

联立式（2.79）、式（2.80）得到

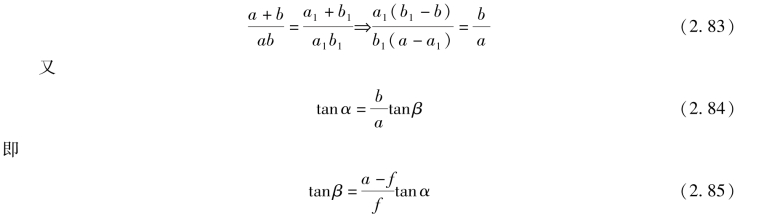
式（2.85）就是著名的斯凯姆普夫拉格（Scheimpflug）条件（也称“沙姆定律”），即激光轴线、物镜主平面、光电探测器基线三者的延长线应该相交于一点或者三者相互平行。满足式（2.79）、式（2.85）的光路即为恒聚焦光路，这样的光路无论被测物体怎样移动，成像光斑都可以准确的落地接收探测器的感光面上，并且成清晰的像。

因为ΔCAO1～ΔCBP1，根据相似三角形各边的比例关系有

由此可以求出被测物的位移与光斑在成像面上的位移间的关系式

当被测物体沿激光轴线靠近激光器时，同样道理可以得到

如果规定x 在被测物体远离激光器时取“+”，而靠近时取“-”，则式（2.87）、式（2.88）就可综合为一式。这样x 用y 可表示为

由式（2.89）可得激光三角测量物像位移关系如图2.19所示。由图可见，随着被测物体y 沿激光轴线远离激光器，其相应的像点在光电探测器上的位置x 变化越来越慢，即放大倍率逐渐变小。而随着被测物体y 靠近激光器，其像点在光电探测器上的位置x 变化越来越快，即放大倍率逐渐变大。

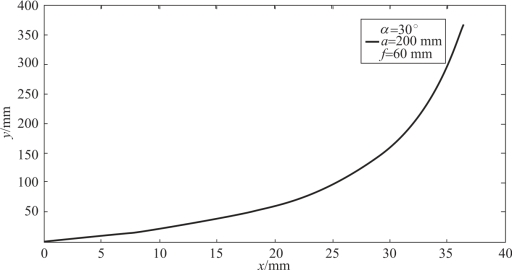
图2.19　物像位移关系图