波前重构算法：实现高效图像处理

光波波前误差是影响发射激光束质量或光学成像质量的最主要因素。斜率测量法不能直接获得光波波前误差的数据，只能测得离散的波前斜率，这就需要从上述离散的波前斜率中恢复出连续的波前形状；同时，测得的波前数据中，通常还包含测量误差，也需要利用波前的全部数据来平滑个别测量点的误差。这两方面的工作都属于波前重构的内容。最普遍的重构波前的方法是区域法和模型法，二者均利用波前的斜率。

1.区域法重构波前

波前上任意两点间的相位存在如下关系：

式中，Δ为哈密顿算子；C 为积分路径，此积分与路径无关。但是，当存在测量噪声的情况下，上一积分是与路径有关的，这就需要寻找更合适的关系式。

设测量得到的波前梯度是g（x，y），其中包括波前真正的梯度Δφ 和噪声n（x，y），即

在最小二乘意义上，有

这是一个变分问题，它满足欧拉方程

式中，为在最小二乘意义上对φ 的估计。

式（2.65）是一椭圆微分方程。在波前相位估计的情况下梯度是已知的，所以变为纽曼（Neumann）边界值问题。在波前估计问题上，存在着唯一解。

最小二乘解的误差是

式可以离散化，可以用N 个点取代连续面问题。这样，一个完整的波前被细分成（N-1）2 个子区间（子孔径）。利用子孔径边界上测量的波前梯度或相位差数据来重构整个波前相位，这一方法称为区域法估计波前相位。

根据测量参数的性质（梯度或相位差）和要求重构波前相位的位置，以及重构算法的不同，可以有许多具体的重构波前的方法。其中按照相位测量点与重构点相对位置的不同，有3 种重要的重构模型，见图2.16。

图2.16　重构网点模型

（a）休晋（Hudgin）模型；（b）弗雷德（Fried）模型；（c）绍契威尔（Southwell）模型
·—待估计的相位点；→↑—测量数据的位置和方向

2.模式法估计波前

区域法估计波前是利用子孔径四邻位置的测量数据估计中心点相位的方法。模式法与此不同，它将全孔径内的波前展开成不同的模式（例如：平移、倾斜、离焦、像散、彗差和球差等）。然后用全孔径内的测量数据去求解各模式的系数，得到完整波前展开式，以重构出波前。

一个完整的波前φ（x，y）可以用多项式F（x，y）展开成

式中，nk 为归一化常数；ak 为待定系数。

为了方便，使Fk（x，y）的平均值为零，即

波前的相位方差为(www.xing528.com)

式中，a0 为相位的平均值。

多项式Fk（x，y）是正交多项式，即

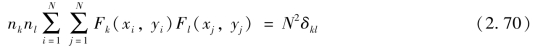
式中，δkl为克罗内克符号。

常用的多项式是Zernike 正交多项式Z（x，y），波前展开式为

上式是波前相位展开式的连续形式。实际上有用的是离散形式，即

为求解展开系数a（a0，a1，…，ak），需要用到波前斜率展开式，从中求得系数a，再根据波前相位展开式（2.67）恢复波前相位。

对式（2.71）微分，即得

式中，εx 和εy 为测量误差。因为波前传感器只能测量子孔径（i，j）内的平均斜率，则

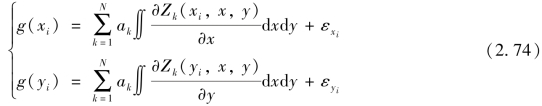
式（2.72）和式（2.73）用矩阵符号表示为

式中，φ 为M 维列向量；Dφ 为M ×N 矩阵；A 为N 维列向量；G 为2M 维列向量；Dg 为2M×N 矩阵；Ag 为N 维列向量。为了方便，令A=Ag。

对于以离散波像差形式表示的原始测量数据，常用Zernike 多项式（表2.3）作最小二乘拟合求出被测波前的形状。对于以离散径向斜率值形式表示的原始测量数据，需要探讨能否改用Zernike 多项式的径向斜率形式作最小二乘拟合，求解出被测波前的形状。

表2.3　泽尼克（Zernike）多项式及其径向斜率多项式

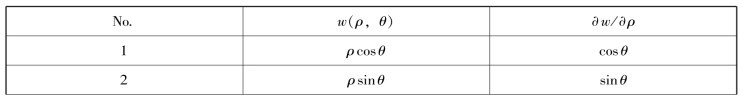
续表

理论分析和计算机仿真结果表明，采样密度足够的情况下，根据已知波前径向斜率分量的离散采样值也完全可以以足够高的精度重构出原始波面的形状；如果径向斜率离散采样值包含有一定的随机误差，也仍能重构出精度与波前径向斜率采样精度相当的波前形状。

由径向斜率重构波前与前述模式法重构波前的方法类似，只需将Zernike 多项式中的各项换成Zernike 斜率多项式的表达形式，波前测量值替换为波前径向斜率测量值data，即

式中，znk 既是Zernike 斜率多项式的各项系数，同时也是重构波前的Zernike 多项式系数。只要采样点数大于多项式项数n，式（2.77）就可写出最小二乘解