影响条纹对比度的因素分析

为进行高精度观测，要求得到的干涉条纹不仅明亮、清晰、稳定，而且亮暗分明，即具有良好的对比度。干涉条纹的对比度定义为

式中，Imax和Imin分别为静态干涉场中光强的最大值和最小值，也可以理解为动态干涉场中某点的光强最大值和最小值。

对于式（2.12），当Imin=0 时K=1，对比度有最大值；而当Imax=Imin时K=0，干涉条纹完全消失。对于目视干涉仪而言，当K>0.75，可以看到对比度较好的条纹。在实际应用的干涉仪中，由于种种原因，所观察到的干涉图样对比度都是小于1 的。

常见影响条纹对比度的因素主要有以下几个方面：

（1）光源的时间相干性和空间相干性；

（2）相干光束的光强不相等；

（3）杂散光的存在；

（4）各光束的偏振状态有差异。

另外还有一些因素，如振动、空气扰动及干涉仪结构的刚性不足，都有可能导致干涉图样的对比度下降，甚至条纹消失。下面分析影响条纹对比度的各项因素。

1.光源单色性与时间相干性

干涉测量中实际使用的光源都有一定的谱线宽度，记为Δλ。如图2.2所示，实线1 和虚线2 分别对应λ 和λ+Δλ 两组条纹的强度分布曲线，其他波长对应的条纹强度分布曲线居于上述两曲线之间。干涉场中实际见到的条纹是这些干涉条纹叠加的结果。

如图2.2中实线3 所示，在零级位置处，各波长的极大值重合，之后慢慢错开。干涉级次越高，各波长极大值错开的距离越大，合强度峰值逐渐变小，对比度逐渐降低。当λ+Δλ 的第m 级亮纹与λ 的第m+1 级亮纹重合后，所有亮纹开始重合，而在此之前是彼此分开的。以上条件可作为尚能分辨干涉条纹的限度，即

图2.2　各种波长干涉条纹的叠加

由此得最大干涉级m=λ/Δλ，因此相应的尚能产生干涉条纹的两束相干光的最大光程差（即光源的相干长度）为

式（2.14）表明，光源的相干长度与其谱线宽度成反比。表2.2列出了一些干涉仪光源的相干长度与辐射亮度的参考数值。表中所列的氦氖（He-Ne）激光器，其相干长度最长，辐射亮度也比同位素灯大10 个量级。

表2.2　几种光源的相干长度和辐射亮度

2.光源大小与空间相干性

干涉图样的照度，在很大程度上取决于光源的尺寸，而光源的大小又会对各类干涉仪的干涉图样的对比度产生不同的影响。

由平行平板产生的等倾干涉，无论多么宽的光源尺寸，其干涉图都有很好的对比度。而杨氏干涉实验只在限制狭缝宽度的情况下才能看清干涉图样。由楔形板产生的等厚干涉图样，则是介于以上两种情况之间。如图2.3所示，光源是被均匀照明的直径为2r 的光阑孔，光阑孔上不同点S 经过准直物镜后形成与光轴不同夹角θ 的平行光束。不同θ 角的平行光束经干涉仪形成彼此错位的等厚干涉条纹，经叠加后形成的干涉条纹如图2.4所示。当光阑孔较小时，干涉条纹的对比度较好；随着光阑孔增大，干涉条纹的对比度下降，直至趋于零。如取对比度降至0.9 为限，可得光源的最大许可半径为

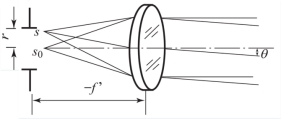
图2.3　等厚干涉仪中的扩展光源

图2.4　光阑孔大小对干涉条纹对比度影响

（a）光源半径很小时，干涉条纹对比度高；（b）光源半径变大时，干涉条纹对比度下降；（c）继续增大光源半径，干涉条纹对比度降为0

可见，光源的最大许可半径正比于准直物镜的焦距f′，反比于等效空气层厚度h 的平方根。空气层厚度越小，光源开孔越可调大，干涉条纹则具有较高的亮度。

在干涉测量中，采取尽量减少光源尺寸的措施，虽然可以提高条纹对比度，但干涉场的亮度也随之减弱，从而不利于观测。如能设法改变参考光路或测量光路的光程，使两束光的等效空气层厚度减薄，可以达到适当增大光源的目的。

3.相干光束光强不等和杂散光的影响

干涉实验中，设两束相干光的光强的关系为I2=nI1，则有

图2.5所示实线表示了干涉条纹对比度K 随两束光束强度比n 的变化。当n=6 时，K=0.7。

图2.5　对比度K 与两束干涉光强比n 的关系(www.xing528.com)

此外，在干涉测试中，还常常伴有非期望的杂散光进入干涉场。例如，光束在干涉仪光学零件表面上的反射、散射等。

设混束两束干涉光路中杂散光的强度均为I′=mI1，这种情况下，

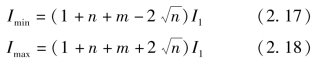
由此得到

当n=1 时，有

可见，在两束光强接近，即光强比n 较小时，杂散光对条纹对比度的影响更为明显。所以，必须重视干涉仪中采取抵制和消除非期望的杂散光的技术措施，主要包括在光学零件表面镀增透膜、设置消杂光光阑、选用带楔角的分光板等。

4.干涉光束偏振状态的不同影响

在使用激光光源的干涉仪中，大都是部分偏振光干涉的情况。如果两束干涉光的偏振态不同，干涉图样的对比度也会降低。为提高干涉条纹的对比度，有时会在干涉仪的出口处安装一个偏振片。下面简要介绍偏振面为任意角度的两束线偏振光的干涉。

如图2.6所示，两束振幅为a1 和a2 的线偏振光的振动分别位于法向量为q1 和q2 的平面上（下文简称平面q1 和q2 上，本节中均使用法向量表征平面），两个振动面之间的夹角为φ。为方便推导，令q1 与直角坐标系x 轴相重合，选取坐标轴方向，使φ 可取0°～90°的任意值。首先，假设两相干光束都是全偏振光，它们都在一个平面p 内振动，并且具有相同的振幅a0。这时，两束光在平面q1、q2 内的分振幅分别为

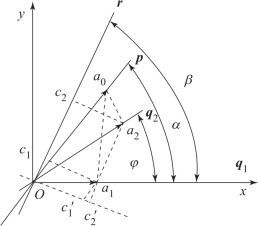
图2.6　两束线偏振光干涉示意图

式中，α 为平面p 和q1 之间的夹角。

如果在干涉仪的出射孔处安装一个检偏片，并使其振动面r 和平面q1 之间的夹角为β，则两支干涉光束的振幅分别为

则

式中，δ 为两个振动之间的相位差。取cosδ 分别为+1 和-1，可得干涉图样对比度为

从上式可以得出结论：

（1）当α=90°+φ 和α=90°，以及β=90°+φ 和β=90°时，K1=0。因为在这些情况下，产生的干涉振动之一的光束的振幅等于0。

（2）当c1=c2 或α+β=φ 时，对比度具有最大值。

可见，采用以适当的方式定向偏振片和检偏器的情况下，可以在平面q1 和q2 之间的夹角φ 为任意值时，得到高对比度的干涉图样。

假设去掉检偏器，这时无论是a1 还是a2 都可以分解为分别位于平面r 和r′上的两个相互垂直的振动，即分解为c1、c′1 和c2、c′2。经过上式类似的推导，得到条纹对比度为

K2 的量值与β 无关。这意味着，在计算K2 时，可以采用相互间呈任意配置的平面r和r′。

假设检偏片安装在最有利的位置上，这时有

假如去掉起偏器（保留检偏器），也就是说，如果平面q1 和q2 上的振动来自自然光，则角α 的任意值都是等概率的，眼睛或其他接收器所感受到的图样对比度取决于K1 的平均值。为了求得这一平均值，需要对α 在0～π 的区间上积分，并将结果除以π，结果为

式中，K3 为两个干涉振动面之间夹角φ 的函数。

为了计算既没有起偏器又没有检偏器情况下的对比度，应该算出由式（2.27）所决定的对比度K2 的平均值。由式（2.27）和式（2.28）可得K2=K1cosφ。由此进一步求得

由上面的计算结果可以看出，把偏振片安装在干涉仪之前（K2）比安装在干涉仪之后（K3）效果更好。可是，当角φ 的量值相当大时，只有采用两个偏振片（其中一个安装在干涉仪的前面，而另一个安装在干涉仪的后面）的情况下，才能得到好的图样对比度。

上述结论是针对干涉光束为全偏光的极限情况得到的，而在干涉仪中通常存在的是部分偏振光。安装偏振片虽然不是必需的，但在许多情况下，可以显著地提高干涉图样的对比度。