光波叠加及复振幅分布研究

本节以两束频率相同、振动方向相同的单色光波相遇为例，研究光波叠加后的复振幅分布。如图2.1所示，设光波分别发自光源S1 和S2，P 点是两光波相遇区域内的任意一点，P 到S1 和S2 的距离分别为r1和r2，则两光波在P 点产生的光振动可以写为

图2.1　光波叠加示意图

式中，a1 和a2 分别为两光波在P 点的振幅；φ1 和φ2分别为两束光波在光源处的初相位。则α1=kr1+φ1，α2=kr2+φ2 分别为两束光波在P 点的初相位，根据叠加原理，合振动为

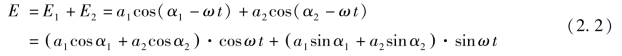
因为a1、a2 和α1、α2 均为常数，所以可令

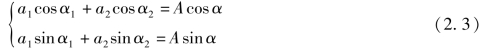
将式（2.3）等号两侧分别平方相加，并化简可得

将式（2.3）等号两侧对应相除可得(www.xing528.com)

因此，由式（2.2）、式（2.3）可得，P 点的合振动仍可写为简谐振动的形式，即

若两束单色光的振幅相等，即a1=a2=a 时，P 点的光强可以写为

当两束光波在P 点的初相位差 （α1-α2）为2π 的整数倍，即α1-α2= ±2mπ（m=0，1，2，…），则P 点的光强具有最大值。

当两束光波在P 点的初相位差 （α1-α2）为2π 的半整数倍，即2π（m=0，1，2，…），则P 点的光强具有最小值。

若光源S1 和S2 的初相位φ1 和φ2 相同，则两束光波在P 点的初相位差（α1-α2）与传播距离差（r1-r2）之间满足关系

式中，λ 为真空中的波长；n 为介质折射率；n（r2-r1）为光程差。

显而易见，在两光波叠加区域内，不同点的光程差可能不同，所以光强也不同。但对于理想的单色光波，即使光程差不同，只要两束光波的位相差保持不变，叠加区域内各点的强度分布也不变。把叠加区域内出现的光强稳定的强弱分布现象称为光的干涉，产生光干涉的光波称为相干光波，光源称为相干光源。