实训五十：PID控制器参数整定实验

1.硬件闭环PID控制实验装置

为了学习整定PID控制器参数的方法，必须做闭环实验，开环运行PID程序没有任何意义。FX的仿真软件不能对PID指令仿真，不能用纯软件仿真的方法来做闭环实验。如果有FX系列的PLC，用硬件组成一个闭环需要模拟量输入模块和模拟量输出模块，此外还需要被控对象、检测元件、变送器和执行机构。例如可以用电热水壶作为被控对象，用热电阻检测温度，用温度变送器将温度转换为标准电压，用交流固态调压器作执行机构。

2.用运算放大器模拟被控对象的闭环实验

可以用以运算放大器为核心的模拟电路见图6-19）来代替现场的被控对象，在实验室组成模拟的闭环控制系统。运算放大器应使用双电源，例如±12V的电源。设置模拟量输入、输出模块的量程为±10V。

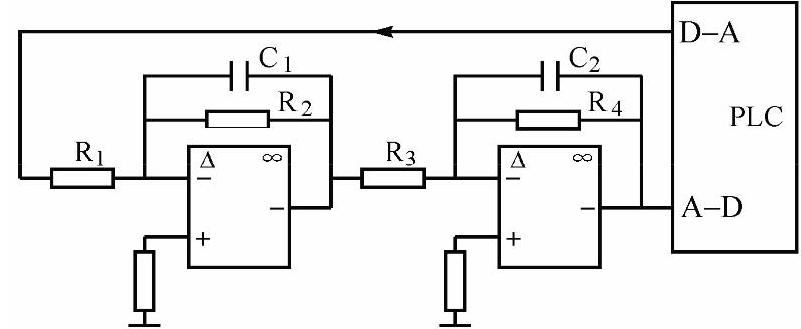
图6-19 模拟被控对象的电路

将运算放大器电路的输出端接到PLC的模拟量输入模块的电压输入端，将PLC模拟量输出模块的电压输出端接到运算放大器电路的输入端，这样就组成了一个模拟的闭环控制系统。

可以用图6-19中的运算放大器电路来模拟一阶惯性环节、两个串连的惯性环节，或串连的惯性环节与积分环节。图中左边的运算放大器电路的传递函数为

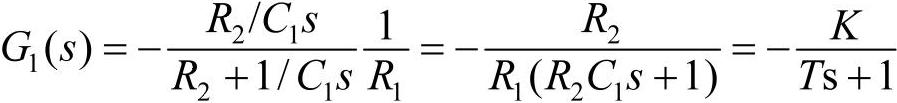
式中K=R₂/R₁,T=R₂C₁，s是拉氏变换中的拉普拉斯算子。右边的运算放大器的传递函数可以用类似的方法求得。

如果断开图中的C₂，则右边的运算放大器变为反相器，其传递函数为G₂(s)=-R₄/R₃。如果断开图中的R₄，则右边的运算放大器变为积分器，其传递函数为G₂(s)=-1/(R₃C₂s)。模拟对象总的传递函数为G(s)=G₁(s)·G₂(s)。电阻和电容的值应取大一些，使传递函数中的时间常数为秒级。可以在电路板上设置DIP开关，用它来改变被控对象传递函数的结构和参数。

3.纯软件闭环PID实验

西门子的S7-300/400 PLC的功能块FB 41是PID控制的子程序，S7-300/400的仿真软件PLCSIM可以对FB 41仿真。此外西门子还提供了一个用来模拟被控对象、检测元件和执行机构的功能块FB 100。用FB 41和FB 100可以组成虚拟的PID闭环控制系统，用计算机对PID控制系统仿真。

通过设置PID控制器的参数，用仿真软件执行闭环控制程序后，观察被控量的变化情况，通过被控量阶跃响应曲线的形状，估算超调量和调节时间等性能指标，就可以判断出控制的品质。可以根据前述的参数整定方法修改PID控制器的参数，直到得到比较理想的控制效果。

作者编写的《跟我动手学S7-300/400 PLC》和《S7-300/400 PLC应用技术》第3版详细介绍了纯软件闭环PID仿真程序的设计方法和做仿真实验的方法。《跟我动手学S7-300/400 PLC》用西门子人机界面的组态软件WinCC flexible的趋势图，显示PID控制的设定值SV和被控量c(t)的曲线。

《S7-300/400 PLC应用技术》第3版使用S7-300/400的编程软件集成的PID控制参数赋值工具来修改PID的参数，显示PID控制的设定值和被控量的曲线。该书详细地介绍了PID控制参数赋值工具的使用方法。本节后面的PID控制的阶跃响应曲线来自PID控制参数赋值工具。

这两本书的随书光盘提供了PID闭环控制仿真程序和仿真所需的全部软件。

根据读者或使用本书的学校的具体条件，可以选择3种实验方式：

1）全部采用硬件的PID控制实验。

2）使用硬件PLC，用运算放大器来模拟被控对象、执行器和检测元件的PID控制实验。

3）S7-300/400的PID控制纯软件仿真实验。

4.PID闭环控制仿真结果介绍(https://www.xing528.com)

图6-20～图6-26给出了PID控制器的主要参数，图6-20中曲线的超调量过大，有多次振荡。将图中的积分时间由2s改为4s，单击PID控制参数赋值工具的工具条上的下载按钮 ，将修改后的参数下载到仿真PLC。与图6-20中积分时间为2s的曲线相比，增大积分时间（减弱积分作用）后，图6-21中响应曲线的超调量和振荡次数明显减小。

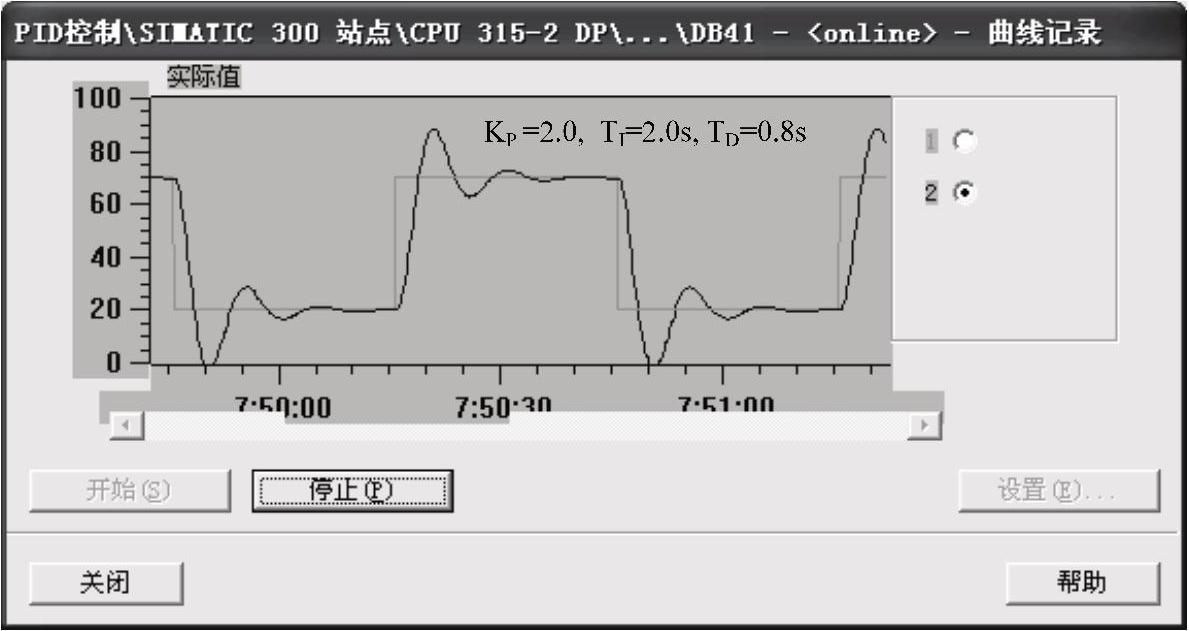
图6-20 曲线记录对话框

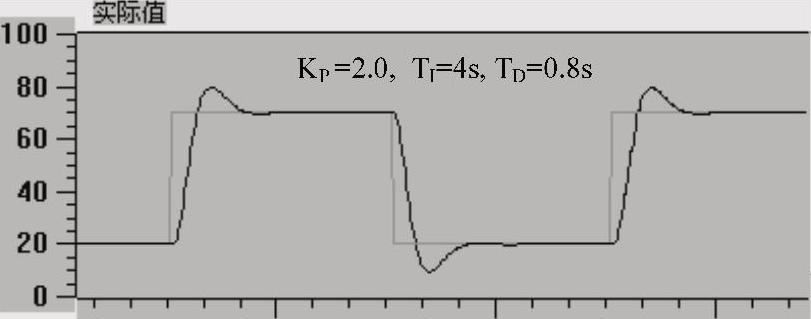
图6-21 PID控制阶跃响应曲线

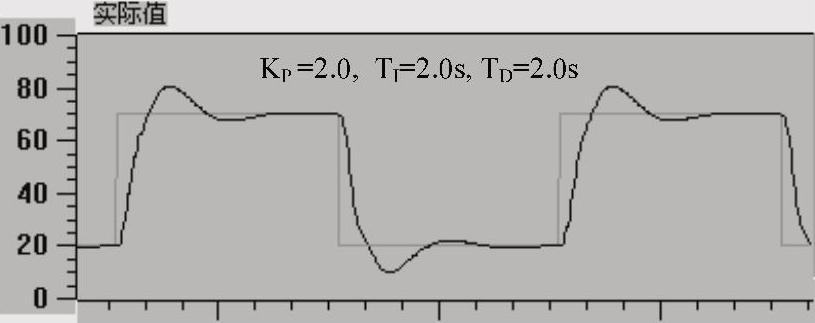
图6-22 PID控制阶跃响应曲线

将图6-21中的积分时间还原为2s，微分时间由0.8s增大为2s。与图6-20中的曲线相比，适当增大微分时间后，图6-22中响应曲线的超调量和振荡次数明显减小。

将图6-22中的积分时间改为8s，微分时间仍然为2s。与图6-20中的曲线相比（积分时间为2s，微分时间为0.8s），增大积分时间和适当增大微分时间后，图6-23中响应曲线的超调量几乎为0，但是付出的代价是第一次上升到稳态值的时间较长。

微分时间也不是越大越好，图6-24的微分时间增大到4s，因为微分作用过强，在误差剧烈变化时，对误差变化的抑制作用太强，曲线上出现了“毛刺”，曲线变得很怪异。这种现象提示应减弱微分部分。

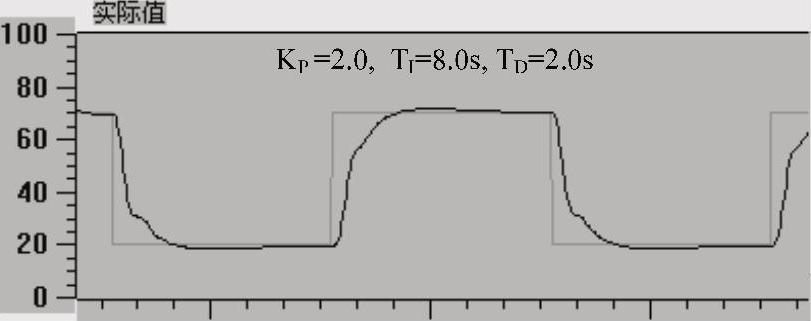
图6-23 PID控制阶跃响应曲线

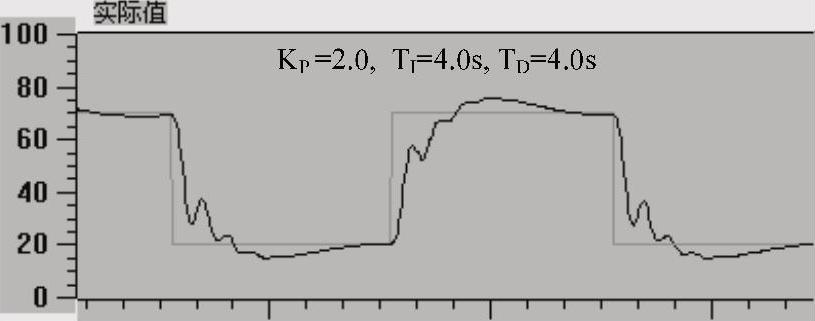
图6-24 PID控制阶跃响应曲线

图6-25和图6-26的微分时间均为0（即采用PI调节），积分时间均为8s。图6-25的比例增益为2.0，图6-26的比例增益为1.0，减小了比例增益后，同时减弱了比例作用和积分作用。可以看出，减小比例增益能显著降低超调量。但是付出的代价是上升时间t_r增大。

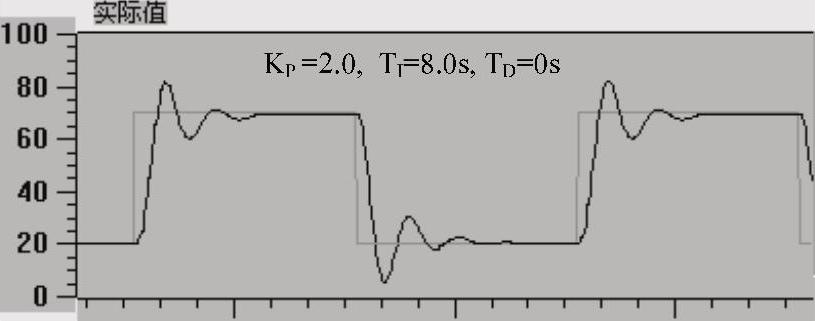
图6-25 PI控制阶跃响应曲线

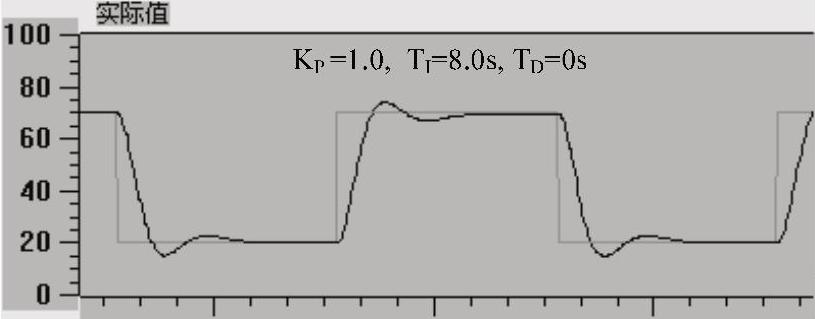
图6-26 PI控制阶跃响应曲线

读者可以修改程序中FB 100（被控对象）的参数，下载到仿真PLC后，调整PID控制器的参数，直到得到较好的响应曲线，即超调量较小，过渡过程时间较短。也可以修改采样周期，了解采样周期与控制效果之间的关系。通过仿真实验，可以较快地掌握PID参数的整定方法。