均匀成核理：非均匀成核现象研究

均匀成核理论告诉我们，晶核在亚稳流体相中各处的成核概率是相同的，同时需要克服相当大的表面能位垒，即需要相当大的过冷度（或过饱和度）才能成核。例如，均匀成核理论预言，水蒸气中冰晶的成核，其临界过饱和度为3.4；水凝固时，其临界过冷度则为40℃。当然，有些已为实验所证实，但是，也发现在许多亚稳流体相中，成核所需要的过冷度（或过饱和度）远低于均匀成核理论所预言的数值。研究发现，由于在这些亚稳态的流体相中总是包含有微量杂质和各种外表面，进行相变的物质系统将通过在杂质或各种外表面上成核，力图减少由于系统表面能增加所造成的障碍，结果是原有的界面被“消除”，而净表面能的变化就可获得某种程度的减少。

由于亚稳相中存在着这些不均匀性，例如各种杂质、容器壁或坑洞等，而这些不均匀性皆有效地降低了成核时的表面能位垒，晶核也就优先在这些不均匀处形成，这就是我们要讲的非均匀成核。凡是能有效地降低成核位垒促进成核的物质统称为成核促进剂。存在成核促进剂的亚稳系统，系统中空间各点的成核概率当然也就不同了。

1.熔体的表面张力——表面能

表面能是指将表面增大一个单位面积所需要做的功，以σ表示之，单位是erg/cm2（lerg=10-7J）。如果作用于液体表面单位长度周界上的一个力，其方向是沿周界的内法线并与界面相切，这样向外拉，于是就增大了液体表面而做了功，在长为1cm的周界上作用一力，此力将周界拉长1cm，使液体表面积增加1cm2，若此力所做功为σerg，则此力大小正好为1N。这个力是用来抵消表面单位长度上的收缩表面之力的。这个力我们称之为表面张力，其单位是dyn/cm（1dyn/cm2=0.1Pa）。表面能的单位经过简化后其单位也可以表示成dyn/cm2。因此，液体的表面能和表面张力的数值与量纲是相同的。以后涉及表面能时往往就用表面张力来代替。

熔体表面张力的大小会直接影响液-固表面的浸润程度。一些熔体的表面张力数值列于表3-5中。其中，B2O3熔体的表面张力很小，这是由于硼熔体中硼氧三角体平面可以按平行于表面的方向排列。这样，熔体内部和表面之间能量差别就比较小。因此，B2O2常常用作降低表面张力的组分。各种氧化物添加剂对熔体表面张力的影响很不相同，如Al2O3、CaO、MgO、SiO2等能提高表面张力；而K2O、PbO、B2O3、Sb2O3、Cr2O3等引入量较大时，均能显著降低熔体的表面张力。

表3-5　熔体的表面张力

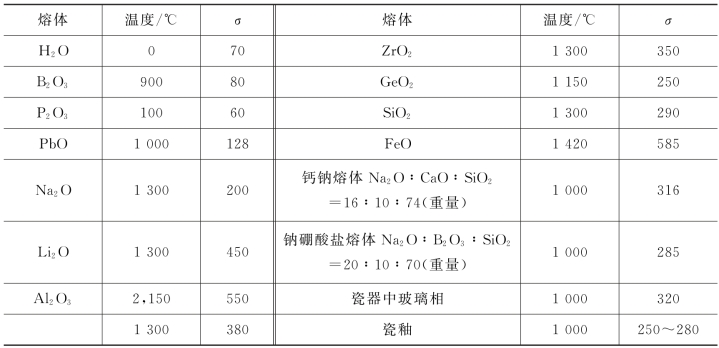
另外，熔体内原子（离子或分子）的化合键型对其表面张力也有很大影响。其规律是：具有金属键的熔体表面张力>共价键>离子键>分子键。当两种熔体混合时，一般不能单纯将它们各自的表面张力值用加合法计算。由于表面张力小的熔体在混合后会聚集在表面上，因此，即使少量的加入也可以显著地降低混合熔体的表面张力。

大多数熔体的表面张力都是随温度升高而降低（负的温度系数）。有资料表明，一般，当温度提高100℃时，表面张力减少1%左右。

2.接触角

为了定量描述相交接处的具体情况，我们引入接触角的概念，先从大家熟悉的液滴开始讨论。

液体与固体表面相接触时，使固体的表面能下降的现象称为浸润。浸润的程度与两相的表面张力有关。

当把一液体滴在固体表面上时，就形成了一个固—液—气系统。平衡时，液滴可能会出现3种不同的情况，如图3-32所示

图3-32　浸润与液滴的形状

（a）不浸润；（b）浸润；（c）完全浸润；液体铺开

浸润程度通常用接触角θ来表示，它是指液体表面张力γLV和固-液界面张力γSL之间的夹角。固—气界面张力γSV是力图把液体拉平，掩盖固体的表面以使表面能得到下降。而液体的表面张力γLV和固-液界面张力γSL是力图使液体变成球形。当平衡时，在三个相的交点处，作用力应达到平衡，可成立下式：

根据式（3-63）可知：①如果γSV-γSL=γLV，则有cosθ=1，θ=0完全浸润，液体在固体表面铺开来，当γSV-γSL>γLV时，θ角也是等于零，相当于图3-28中（c）的情况；②如果γSV-γSL<γLV时，则有1>cosθ>0，θ<90，固体能被液体浸润，相当于图3-28中（b）的情况；③当γSV<γSL时，则cosθ<0，θ>90，固体不被液体所浸润，相当于图3-28中（a）的情况。

若干两相系统的接触角及界面能如表3-6所示。

表3-6　几种二相系统的接触角及界面能

我们再来看看在液相中于基底上形成一固相晶核的情况，如3-33图所示。

图3-33　非均匀成核示意图

在以下的讨论中，认为表面张力在数值上就等于表面自由能，同时定义如下：

σLS——晶体与流体相之间的比表面自由能；

σSB——晶体与基体之间的比表面自由能；

σLB——基底与流体之间的比表面自由能。

在三相交接点处，为了满足力学平衡条件，同样有：

在无机材料中，主晶相与其同一系统的低共熔物所组成的系统，都是浸润的。例如，Al2O3被MgO-Al2O3-SiO2系统的低共熔物所浸润。

3.成核功及临界半径

在讲非均匀成核时，多是以球冠形晶核的形成为例来说明。当然，如果晶核不是球冠形的，对下述的讨论及结论也并无实质性的影响。

若假定形成晶核的固体基底为一平面，诸界面能亦为各向同性，流体于基底上形成如图3-33所示的一个球冠形晶核。

由初等几何可以求出球冠状晶核的体积Vs、晶核与流体相之间的界面面积ALS及晶核与基底之间的界面面积ASB，即

式中，r为球冠状晶核的半径。当球冠状晶核在基底上形成之后，系统中吉布斯自由能的变化为(www.xing528.com)

此即球冠状晶核的成核功，以“*”表示之。

将式（3-65）代入式（3-66），并利用式（3-64）的关系，可以得到：

将式（3-67）对r求微商，并令=0，可得球冠状晶核的临界曲率半径rc为

将式（3-68）中的rc值代入式（3-67），则可求得形成球冠状临界晶核所需要的成核功：

比较式（3-53）和式（3-69），可以得到。由于接触角0°≤θ≤180°，故-1≤cosθ≤1。由f（θ）的表示式可以看出，有0≤f（θ）≤1，因此可得到：

式（3-70）是一个很重要的关系式，它告诉我们为什么非均匀成核要比均匀成核容易些的原因。非均匀成核所需要的能量起伏较小，所以它可以在较小的过冷度下发生。

非均匀成核时的成核速率表达式与均匀成核的相似，只是由于，才使得非均匀成核在较小的过冷度下获得较高的成核速率。图3-34为均匀成核与非均匀成核时的N-ΔT曲线示意图。曲线表明，非均匀成核的成核速率在过冷度不大时的增长较为平缓，与最大成核速率相对应的ΔT较小，而在成核速率达到最大值后曲线下降并且中断，可以认为是由于非均匀成核的“基底”有限，在成核过程中它们不断被消耗而迅速减少所致。曲线也表明，当非均匀成核的成核速率达到相当可观的程度时，均匀成核仍是微不足道的。究其原因，就是因为不溶性固体（杂质、坩埚壁等）基底平面的存在，直接影响晶核的比表面自由能，从而影响晶核的形成功。

图3-34　成核率随过冷度变化的曲线

如果将式（3-68）代入临界球冠状晶核表面自由能的表达式中，可以得到：

比较式（3-69）和式（3-71），可知：

这一结论同均匀成核时完全相同。

由式（3-68）和式（3-71）可以看出，非均匀成核的临界半径同均匀成核的临界半径是完全相同的。这并不奇怪，因为弯曲界面的平衡条件告诉我们，只要相变驱动力的条件相同，则表面上任何一部分的平衡就仅仅取决于该部分的曲率半径，而与其表面形状无关。

下面，对式（3-69）进行几点讨论：

（1）当θ=0°时，f（θ）=0，）=0，这是完全浸润的情况，此时在无过冷度的情况下晶体即可成核生长，即在基底平面上形成晶核所需要的成核功为零，在基底上的流体相可直接转变成晶体。这也是比较容易理解的，因为θ=0°，表示完全浸润，在基底上将覆盖一层具有宏观厚度的晶体薄层，这种情况可等价于籽晶生长或同质外延。

（2）当θ=180°时，f（θ）=1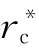，（）=ΔGc（rc），这是完全不浸润的情况，此时晶核只与基底相切于一点；球冠状晶核完全变成球形晶核，基底对成核不再起任何催化作用。

（3）0°<θ<180°时，-1<cosθ<1）<ΔGc（rc），这是比较一般的情况。此时，基底平面上形成晶核所需的成核功小于在自由空间形成球状晶核所需要的成核功。

由于含有一定数目原子的晶核，它在基底表面形成一个球冠体时要比形成一个体积与球冠体体积相同的完整球体具有更大的曲率半径，因此在一定的过冷度下，具有临界半径的附着在基底表面上形成球冠体的晶核，要比在液相中形成一个具有同样的曲率半径的球体晶核所含的原子数目少很多。所以，当附着在适当的界面上成核时，体积较小的晶核便有可能达到临界半径，因此在较小的过冷度下，非均匀成核便开始了。

当在基底表面形成球冠状晶核时，在球冠体体积一定的情况下，接触角越小，球面的曲率半径将越大。因此，在一定的过冷度下，液相中可能出现的最大晶核的体积折合成同样大小体积的球冠体时，球冠体的曲率半径将随θ角而异；θ角越小，与其相应的曲率半径将越大，这样，在较小的过冷度下便可出现达到临界半径条件的晶核。图3-35为有不同的接触角时过冷度与曲率半径r的关系。它们与临界半径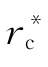和ΔT的关系曲线的交点，即为该θ角相应的成核过冷度。从图3-35中可知，θ角越小，成核过冷度越小，即表示这样的基底界面对成核的催化效能就越高。但上述情况必须有几个先决条件，首先是接触角和温度无关，其次是基底面积要大于晶核接触所需要的面积，最后是晶核和基底的接触面为平面。

由此可见，在生长系统中具有不同接触角的基底材料在成核过程中所起的作用是不同的。据此可以根据实际需要来选择基地材料。例如，为了防止在坩埚和容器壁上结晶，可使用接触角接近180°的坩埚材料。又如在外延生长中，则尽量选用接触角接近于0°的材料作为基底。当然，这里强调的原则是来自成核理论，实际上坩埚或基底材料的选择还要考虑其他许多重要因素的影响。

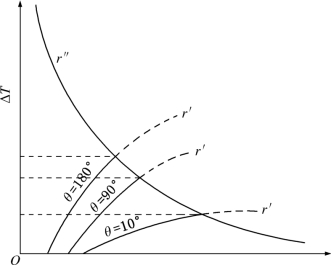
图3-35　均匀成核的成核过冷度与接触角的关系

下面我们来讨论质及形状对非均匀成核的影响。

从上述分析可以看出，晶核与基底之间的接触角是一个很重要的参数。但是究竟有哪些因素影响接触角的大小，目前还不太清楚。

从非均匀成核的成核功表达式可以看出，接触角趋于零时，成核的效能最高，甚至在没有过冷度的情况下也能成核。从式cosθ=可知，当θ→0°时，cosθ→1，即σSB趋于最小，因为通常总是σLB>σLS，这是由于液体和晶核间的原子排列较为接近的缘故。为使cosθ不出现负值，σSB应小于σLB，而且是越小越好，因为σSB越小，则cosθ值越有可能趋近于1。因此，晶核和基底间的表面能越小，就越有利于非均匀成核。根据表面能产生的原因，不难理解，两个相互接触的晶面结构（点阵类型、晶格常数、原子大小）越近似，它们之间的表面能就越小，即使只在接触面的某一方向上结构排列配合得比较好，也会使表面能有所降低。这个规律称为“结构相似，尺寸相似”原理，也称为点阵匹配原理。凡是满足点阵匹配原理的界面，就可能对成核起到催化作用。通常用错位度δ来表示界面上晶核原子与基底原子相互间的匹配情况，即δ=，式中，ac为基底的晶格常数；aN为晶核的晶格常数。

δ值越小，说明两者匹配得越好，其间的表面能就越低。因此，非均匀成核的过冷度也就越低。当δ值很小时，过冷度ΔT与δ之间有如下关系：ΔT∝δ2

有许多实验证明，如果单纯从晶体学的角度来认识上述问题是很不全面的。例如研究发现，纯金小液滴在碳化物或氧化物基底上成核时，尽管氧化物在结构及晶格常数方面与金差别较小，但促进非均匀成核的作用却远不及碳化物。为此有人提出了一种静电作用理论，认为表面能中含有一项恒为负值的静电能，当基底导电性较高时，静电能的绝对值越大，从而可以使晶核和基底间的表面能越小。这种基底促进非均匀成核的作用较大。碳化物之所以有较强烈的促进成核作用，正是由于它的导电性较好。

另外，假若供成核的界面不是平面，而是曲面，则界面的曲率大小与方向（凸、凹）会影响界面的催化效果。图3-36表示在三个不同形状的基底界面上形成的三个晶核，它们具有相同的曲率半径和相同的θ角，但三个晶核的体积却不一样。凸面上形成的晶核体积最大，平面上次之，凹面上最小。由此可见，在曲率半径、接触角相同的情况下，晶核体积随界面的曲率不同而不同。凹面成核效能最高，它的成核过冷度比之平面、凹面上的成核过冷度都要小。

图3-36　θ角与曲率半径相同时，不同类型面上形成的核的体积

（a）凹面；（b）凸面；（c）平面