相变驱动力的特点和应用

气相生长系统中的过饱和蒸汽、熔体生长系统中的过冷熔体以及溶液生长系统中的过饱和溶液都是亚稳相，亚稳相都具有较高的吉布斯自由能，它要使自己的自由能降低，就要过渡到稳定相，这里的稳定相就是晶相。系统之所以能从亚稳相过渡到稳定相，就是因为这两者之间存在着吉布斯自由能的差值，即存在有相变驱动力。

1.相变驱动力的一般表达式

驱动旧相向新相转变的力是什么？它有多大？这是问题的关键，因为此力的大小直接决定了相变速度的快慢。

前面我们已经说过，晶体生长过程就是固-液界面向流体中推移的过程，伴随这一过程发生的则是系统的吉布斯自由能的降低。如果固液界面的面积是A，在驱动力的作用下，它向流体中推进了Δx的垂直距离，这一过程的发生使系统的吉布斯自由能降低了ΔG。如果我们假定界面上单位面积上所受的驱动力为f，则上述过程驱动力做的功为f·A·Δx，驱动力所做的功就等于系统吉布斯自由能的降低，即

式中负号表示吉布斯自由能的减少。于是有

从上式可以看出，生长驱动力在数值上就等于生长单位体积的晶体所引起的系统吉布斯自由能的降低。式中，ΔV=A·Δx，如果令晶体的密度为ρ，晶体的摩尔分子量为M，摩尔数为n，则式（3-29）就可写成：

式中，Δμ是生成一摩尔晶体在系统中引起的吉布斯自由能的降低值。

一摩尔晶体中若有N个原子，而每一个原子由流体相转变成晶体相所引起的吉布斯自由能降低为Δg，则有Δμ=N·Δg，代入式（3-30），f=-。对于确定的晶体，在一定的温度和压力下为常数，并且可以证明，ΩS是每一单个原子的体积。于是有

式（3-31）便是相变驱动力的一般表达式，为了方便，有时把Δg也称为驱动力。若Δg<0，则f>0，表明f指向流体，此时的驱动力为生长驱动力，流体相为亚稳相；若Δg>0，则f<0，表明f指向晶体，此时的驱动力为熔化、升华溶解驱动力，晶体相则是亚稳相。

2.气相生长系统中的相变驱动力

在气相生长系统中，假设在温度为T0、蒸汽压为P0时，气相—晶体两相达到平衡。若保持温度不变，蒸汽压由P0增大至P1，此时的蒸汽系统处于亚稳态，它就有凝结的趋势，P1为此时的过饱和蒸汽压。

根据热力学知识，吉布斯自由能G的微分表达式可表示成dG=-SdT+Vdp。式中，S为系统的熵，V为系统的体积。

由状态函数的性质可知，ΔG只决定于系统的始态与终态，而与路径无关。所以系统由T0P1恢复到T0P0可以认为是等温压缩过程。由于保持了温度不变，所以系统的蒸汽压由P1降至P0时，系统的吉布斯自由能改变为

如果假定蒸汽为理想气体，则一摩尔理想气体的状态方程为V=，代入式（3-32），则得到：

式中，R为气体常数，式（3-33）表明一摩尔的蒸汽在温度为T0时转变成一摩尔晶体时，其系统吉布斯自由能的改变量。

在一摩尔晶体中有N0（即阿伏加德罗常数）个原子，若每一个原子由蒸汽相转变为晶体相时，引起系统吉布斯自由能的降低用Δg表示，则有Δμ=N0Δg。于是，式（3-33）就可以写成：

如果定义a=为系统的蒸汽压饱和比，σ=a-1为系统蒸汽压的过饱和度，同时考虑到R=N0k，k为玻尔兹曼常数。当过饱和度较小时，ln（1+σ）作幂级数展开ln（1+σ）=…则式（3-34）即可简化为

通常也称Δg为单个原子从蒸汽相转变成晶体相的相变驱动力。或将式（3-35）代入式（3-31），得到驱动力为

3.溶液生长系统中的相变驱动力

在溶液晶体两相平衡系统中，假设溶液的饱和浓度为C0。在等温等压条件下，将溶液的浓度由C0增大至C1，则此时的溶液处于亚稳态，C1即为溶液的过饱和浓度，如果晶体处在这样的溶液中，无疑它是会生长的。

根据热力学知识，理想溶液（稀溶液）溶质i的化学势为

式中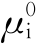——纯溶质i的化学势；(www.xing528.com)

　　C——溶液溶质的浓度。

如果令T0、P0、C0分别表示溶液—晶体两相达成平衡时的温度、压强和溶液的饱和浓度，则由式（3-37）可得：

根据相平衡条件，当溶液晶体两相平衡时，溶质i在溶液中和晶体中的化学势必须相等，即

设想在保持系统温度（T0）和压强（P0）不变的情况下，系统的浓度由C0增大至C1，则此时的溶液为过饱和溶液，它有析出晶体的趋势。在过饱和溶液中溶质的化学势为

综合式（3-39）和式（3-40），可知由浓度为C1的过饱和溶液中生成1mol晶体时，其系统的吉布斯自由能的降低为

同式（3-35）的处理方法类似，同样可以求得：

这就是单个溶质原子由溶液相转变为晶体相所引起的系统吉布斯自由能的降低。若在溶液生长系统中，生长的晶体为纯溶质构成，将式（3-42）代入式（3-31），得溶液生长系统的驱动力为

4.熔体生长系统中的相变驱动力

当结晶物质处在熔点温度Tm时，熔体与晶体结晶物质两相呈热力学平衡状态，此时两相间无相变驱动力，晶体处在既不熔化也不生长的状态。当熔体的实际温度T低于Tm时，熔体则处于亚稳态，此时，由于晶体与熔体的吉布斯自由能不等，在两相间就存在相变驱动力，熔体相有向晶体相转变的趋势。我们定义ΔT=Tm-T为熔体的过冷度。

当熔体与晶体两相处于平衡态时，熔体与晶体的摩尔吉布斯自由能相等，即

根据吉布斯自由能的定义，可以得到：

式中，ΔH（Tm）、ΔS（Tm）分别代表温度为Tm时晶体与熔体两相中摩尔焓的差值和摩尔熵的差值。

由于在晶体生长过程中释放出的相变潜热等于系统中焓的减少，故而有

式中，Lm为摩尔相变潜热。由式（3-45）可以得到，相变发生时，两相摩尔熵的差值与相变发生时的温度的乘积就等于摩尔相变潜热。所以，当结晶物质处在熔点Tm时，熔体与晶体的摩尔熵的差值即为

当系统处在温度T时，由于T<Tm，熔体相与晶体相的吉布斯自由能不等，其差值为

式中，ΔH（T）和ΔS（T）分别代表温度为T时，熔体相与晶体相之间的摩尔焓的差值和摩尔熵的差值，它们都是温度的函数。在熔体生长系统中，一般情况下，认为T只略低于Tm，即过冷度ΔT较小，因而可以近似地认为ΔH（T）≈ΔH（Tm）和ΔS（T）≈ΔS（Tm），于是，将式（3-46）和式（3-47）代入式（3-48），得到：

因而温度为T时单个原子由熔体转变为晶体时吉布斯自由能的降低为

式中，lm=为单个原子的熔化潜热。于是将式（3-50）代入式（3-31），可得熔体生长的驱动力为

在通常的熔体生长系统中，式（3-51）已经足够精确了。但是在晶体与熔体的定压比热相差较大时，或过冷度较大时，驱动力更为精确的表达式为

式中，Δcp=为两相定压比热的差值。当Δcp较小及T和Tm比较接近时，式（3-52）退化为式（3-50）。