相变的基本条件：原理与应用

晶体生长属一级相变过程，因此结晶过程也同其他相变过程一样，需要满足一定的基本条件。

1.结晶的热力学条件

结晶为什么必须在过冷的条件下进行，这是由热力学条件所决定的。热力学第二定律告诉我们，在等温等压条件下，物质系统总是自发地从自由能较高的状态向自由能较低的状态转变。也就是说，只有伴随着自由能降低的过程才能自发地进行，或者说，只有当新相的自由能低于旧相自由能时，旧相才能自发地转变为新相。

自由能G可用下式表示：

式中，H——热焓；

　　T——绝对温度；

　　S——熵。

在可逆过程中有下式：

式中，Q为环境与体系间的热量交换值。

由式（3-21）可以写出：

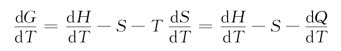
等压条件下dH=dQ，于是得出：

将式（3-23）积分得某一温度时系统的自由能为

式中，G0为绝对零度时的自由能，相当于绝对零度时的内能U0，由于dQ=cpdT，故式（3-22）可表示为

式中，cp为定压比热。将式（3-25）代入式（3-24），可得：

式（3-25）和式（3-26）表明，由于体系的熵恒为正值，且随温度的上升而增加，自由能却随熵的增加而降低。将自由能与温度的变化关系绘成曲线，如图3-24所示。

(www.xing528.com)

图3-24　固液系统的GT关系图

从图中看出，液相与固相自由能随温度变化的曲线各不相同。这是由于液相的比热比固相比热大。因此，液相自由能随温度升高而下降的速率比固相的要大，也就是说液相曲线比固相曲线有更大的斜率。同时，在绝对零度时固相的内能比液相的内能要小。因此，固相曲线的上起点位置较低。基于上述分析可以认为，液相与固相的自由能与温度的变化曲线必然在某一温度下相交，两条曲线交点对应的温度便是该材料的熔点Tm，，此时GL=GS，ΔG=0。液相与固相共存，体系处于热力学平衡态，交点对应的温度Tm即为理论结晶温度。因此，当温度低于Tm时，固相自由能低于液相自由能，则液相会自发地转变为固相。这就是结晶的热力学条件。

在温度低于Tm条件下，有GL>GS，其差值为

若近似地假定液相、固相的密度相同，并令H、S分别为单位体积物质的热焓及熵，则ΔG即为单位体积物质固相与液相自由能的差值，记为ΔGV。只有ΔGV为负值时，固相才是稳定相。我们称负值的ΔGV是结晶驱动力。

由式（3-27）可以导出，当温度T=Tm时，则

在恒温、恒压条件下，TmΔS=ΔQ=-Lm。假定在熔点温度Tm以下，液相、固相自由能随温度变化的速率相差不大，可近似地认为，当体系过冷到某一温度进行相转变时，有

Lm为溶化潜热，代入式（3-27），并由ΔGV代替ΔG，于是：

式（3-28）说明一个很重要的规律，即液相只有在过冷度ΔT>0的条件下，才能保证其自由能差ΔGV<0，而过冷度ΔT越大，则自由能差ΔGV值也就越大，结晶驱动力也就越大。这就从热力学条件出发，进一步说明了过冷是结晶的必要条件。

2.结晶的结构条件

结晶是晶核形成与长大的过程。那么，晶核从何而来，这是一个和液相结构有关的问题，因此我们首先要了解一下液相结构的一些特征。

液体介于气体和固体之间，大量的实验数据证明它更像固体，特别是在接近熔点时的情况更是如此。例如，通过对液态金属的X射线衍射研究可知，液态金属具有与固态金属相似的结构，在配位数及原子间距等方面相差无几，如表3-3所示。

表3-3　液态与固态金属X射线衍射结果比较

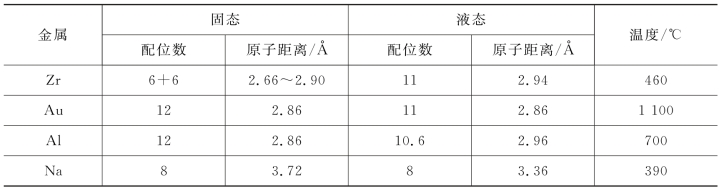
进一步研究认为，液态的结构从长程（整体）来说，原子排列是不规则的，而在短程（局部）范围内存在着接近于规则排列的原子集团，如图3-25所示。这种微小的规则排列的原子集团，称为短程规则排列。

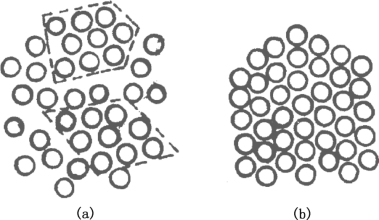
图3-25　金属结构示意图

（a）液态；（b）固态

晶核是由溶质的分子、原子或离子组成的。由于这些粒子每时每刻都在不停地快速运动着，所以又可以把这些粒子叫做运动单元，即使是在新相与旧相处于平衡的状态下，对于极微小的任一空间的任一瞬间而言，各运动单元的位置、速度、能量等也都在迅速地变化着。但就宏观而论，由于这种波动太快也太小，以致于我们测量到的物理量只是它们的时均值。这种波动就是通常所说的能量起伏和结构起伏。正如晶格理论指出的那样，在接近熔点的液体中，由于结构起伏（也称为相起伏）的存在，才使一个运动单元有可能进入另外一个运动单元的力场中，从而结合在一起，构成短程规则排列，这种短程规则排列就成为新相的生成基元团，虽然有的基元团又很快“解体”了，但它们确实能结合在一起。这些大小不同、存在时间很短、时聚时散的基元团具有和晶体固相相似的结构。在这些基元团之间存在着一定的“自由空间”，或者是模糊的边界。基元团实际上就是结晶过程的晶胚。由此可知，结构起伏是液体结构的重要特征之一，它是产生晶核的基础。综上，过冷是结晶的基本条件，因为只有过冷才能造成固相自由能低于液相自由能的条件；也只有过冷才能使液相中短程规则排列结构成为晶胚。