组分过冷的临界条件

拉特（Rutter J.W.）和查默斯（Chalmers B.）于1953年首先对组分过冷进行了系统的研究，并提出了组分过冷的概念。组分过冷现象和枝晶生长都是推动界面稳定性理论发展的主要实验依据。正因为组分过冷是晶体生长中最重要的问题之一，所以有人建议应该把“组分过冷”这个词刻在每一个晶体生长实验室的门上，时刻提醒人们注意。从事人工晶体生长的工作者都十分关心如何改变工艺条件以控制组分过冷的出现，下面我们来讨论产生组分过冷的临界条件。

在上一节中我们已经了解到，由于固液界面前沿溶质边界层的形成，因而造成溶质边界层内熔体凝固点的降低，使得在固液界面前沿形成一狭窄的过冷区，在过冷区内熔体的实际温度低于熔体的凝固点。如果我们提高固液界面处熔体中的温度梯度，即增加温度分布曲线的斜率，使之与凝固点曲线在界面处相切，如图3-8（e）中虚线所示，这样就能保证在溶质边界层内熔体的实际温度高于其凝固点，当然也就不会出现组分过冷了。于是，温度分布曲线与凝固点曲线相切就是不出现组分过冷的临界条件。下面我们就来求出这一条件的数学表达式，从而建立工艺参量和物性参量与组分过冷的关系。

1.工艺参量与物性参量的影响

假设：固液界面为平面，且平行于等温面。由于忽略了动力学效应，可以认为固液界面就是温度等于凝固点温度Tm的等温面。从而得到溶质边界层中溶质浓度的CL（x）与距界面距离x的关系式：

式中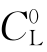——熔体中溶质的平均浓度；

　　k0——溶质的平衡分凝系数；

　　V——生长速率；

　　D——溶质在熔体中的扩散系数。

在熔体生长系统中，溶液的凝固点是溶质浓度的函数，一般情况下，其间的关系也并非是线性的。不过对微量溶质而言，可以近似地认为溶液的凝固点和溶质浓度之间的关系为线性的。若纯物质的熔体（溶剂）的凝固点为T0，令液相线的斜率为m，熔体中溶质分布用CL（x）表示，这样就可以得到熔体中溶液凝固点是关于溶质浓度的表达式：

式中，mCL（x）表示溶液中溶质改变单位浓度所引起的凝固点温度的变化，其数值决定于溶液系统的性质，即决定于溶质与溶剂的性质。经验表明，存在有两类溶质，一种溶质是提高了溶液的凝固点，即m为正值，另一类溶质则降低了溶液的凝固点，即m为负值。我们所要讨论的就是属于这一类的溶质。

只需将式（3-3）代入式（3-4），就可以得到溶质边界层内的凝固点曲线，即凝固点T（x）是关于距界面距离为x的关系式：

通过对一维稳态温度场的分析，得知在固液界面前沿的狭窄区域内，温度分布曲线可近似地看作为直线。若令该直线的斜率为G，则熔体中的实际温度分布为

T（0）即为固液界面处（即x=0）溶液的凝固点温度。由式（3-5）可知，在固液界面处（x=0），有

将式（3-7）代入式（3-6）即可得到熔体中的实际温度分布T（x）：

式（3-5）代表熔体中的凝固点曲线，式（3-8）代表熔体中实际的温度分布。由图3-4（e）可知，当这两条曲线相交于两点时，就会有组分过冷区出现，如果两者在x=0处相切，就不会有组分过冷区出现了。实际上，这就给出了避免组分过冷的临界条件。由式（3-5）对x求微商，并令x=0，可得到凝固点曲线在固液界面处的斜率，即

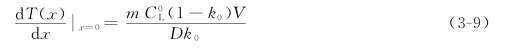
当实际温度分布曲线（直线）的斜率，即温度梯度G等于或大于凝固点曲线在固液界面处的斜率即如式（3-9）时，体系将不会出现组分过冷，于是有

式（3-10）给出了不出现组分过冷的临界条件，它最早是由泰勒等人导出的。式之左边是可以调节的工艺参量：熔体内的温度梯度和生长速率V。式之右边为系统的物性参量：溶液中溶质的平均浓度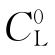、液相线斜率m、溶质的平衡分凝系数K0以及溶质在溶液中的扩散系数D。对于确定的生长系统来说，这些参量是不能任意调节的。

由式（3-10）可以看出，对于确定的溶液系统而言，稳态凝固时该式的右端为一常数，当固液界面前熔体中的温度梯度G和生长速率V之比值大于或等于此常数时，就可避免组分过冷的产生，或者说，对于确定的生长系统，G越大，V越小就越不易出现组分过冷。

对不同的溶液系统而言，溶液中的溶质浓度越小，液相线的斜率越小，平衡分凝系数K0越接近于1，则越不易出现组分过冷。在极限情况下，若=0，即溶液中无溶质；或者是k0=1，液相中溶质完全扩散，即固液界面处不会形成溶质边界层，则式（3-10）之右端恒为零，此时不论G/V的比值的大小如何，必然都使式（3-10）成立，即决不会出现组分过冷。

研究光滑平界面向胞状界面的转变，可以从实验上定量检验产生组分过冷的临界条件，即式（3-10）的正确性。对于确定的生长体系，不出现组分过冷的临界条件可以写为

(www.xing528.com)

这显然是一条通过原点的直线。1955年，有人研究了以锡为溶质，铅为溶剂的溶液系统，对不同的C0L值从实验上求得了转变为胞状界面的G/V的临界比值，其结果示于图3-9中。结果表明实验与理论符合得很好。尔后，1956年在含锡、银、金的铅中，1959年在含铅、铋、锑的锡中都得到了和理论相一致的结果。而后者的平衡分凝系数k0>1。

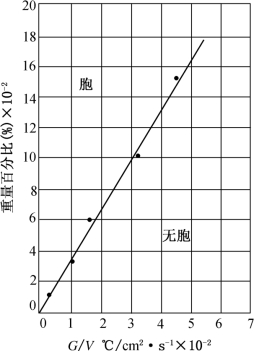
图3-9　组分过冷临界条件的实验验证

下面，我们进一步讨论组分过冷层的厚度，因为组分过冷层的厚度关系到胞状界面上胞的大小。由图3-8（d）可知，组分过冷层的厚度δ就是凝固点曲线与实际温度分布曲线的交点坐标。它可以由式（3-5）和式（3-8）求得：

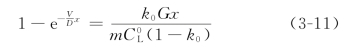
上式中异于零的实数解就给出了组分过冷层的厚度。

作为一个例子，我们将以锡为溶质、铅为溶剂的系统计算结果表示于图3-10中。从图中可以看出，当温度梯度G=30℃/cm、生长速率V=0.002cm/s时，组分过冷层的厚度等于零，即不出现组分过冷；而当V=0.005cm/s时，δ=3.6×10-2cm；当V=0.017cm/s时，δ=5×10-2cm，可以看出，当G不变时，V越大组分过冷层的厚度就越厚。同样，当V不变时，G越大，则组分过冷层越薄。这充分表明，增大温度梯度G，减小生长速率V，对克服组分过冷显然是有益的，实验结果和理论分析是一致的。

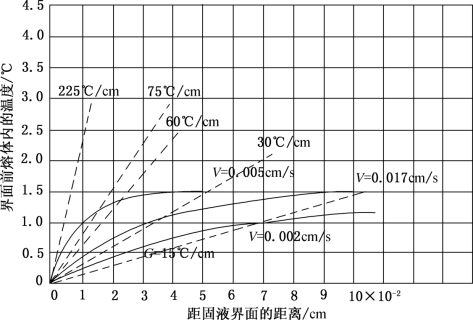
图3-10　不同G、V的含Pb的Sn中组分过冷层的厚度

2.对流传输的影响

前面所讨论的组分过冷理论，只适用于溶质扩散是唯一传输机制的情况。下面我们来考虑对流效应（包括自然对流和强迫对流）对产生组分过冷临界条件的影响。

正如边界层理论认为的那样，在边界层中溶质的传输机制仍为扩散机制。而在边界层之外的熔体中，由于对流效应的存在，可以认为溶质的分布是均匀的，对流效应完全体现在对溶质边界层厚度的影响上。

当一个系统存在对流时，溶质边界层δc中的溶质分布为

将式（3-12）代入式（3-4），即得到在考虑了对流效应之后溶质边界层中的凝固点曲线：

式（3-5）和式（3-13）所表示的都是边界层中凝固点关于距界面距离x的关系，所不同的是前者描述的是只存在扩散的情况，而后者是同时考虑到有对流效应的影响。

同前面的处理方法类似，我们来求出凝固点曲线在固液界面处的斜率，即对式（3-13）求微商，并令x=0，则有，考虑到存在对流效应时，分凝系数应该采用有效分凝系数kef，即kef=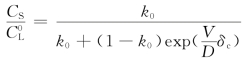，将kef代入上式，即可得：

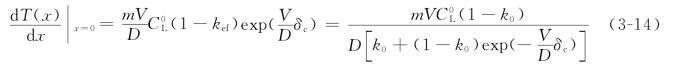
同样，在固液界面前沿狭窄的区域内，温度分布曲线可近似地看作直线，其斜率即为G，所以不产生组分过冷的临界条件就是：

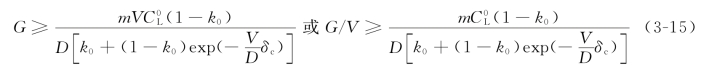
式（3-15）是在考虑了对流之后，不产生组分过冷的临界条件，它是赫尔（HurleH.T.J）于1961年导出的。实际上，它只不过是式（3-10）的推广，如果系统中溶质的传输只是通过扩散进行的，其溶质边界层的厚度趋于无穷，即δc→∞，则式（3-15）自然也就还原成式（3-10）了。

式（3-15）适用于任何液流状态，包括自然对流、各种搅拌引起的强迫对流，以及同时存在自然对流和强迫对流的状态。但关键在于必须求出不同工艺情况（即不同的液流状态）下的溶质边界层的表达式，才能应用式（3-15）分析具体问题。然而迄今为止，只有在提拉法中旋转晶体下获得了溶质边界层厚度的近似表达式，例如对斯密特数较大的流体，如氧化物熔体。

上面，我们已经讨论了溶质在两种传输机制下产生组分过冷的情况。原则上讲，避免组分过冷是十分简便的，降低生长速率，加大晶体旋转速度，降低溶质浓度及加大固液界面附近熔体中的温度梯度等均可实现上述目的。然而实际上问题并不是那么简单，首先人们往往需要具有一定掺质浓度的晶体，当然也就不能随意降低原料中溶质的浓度。同时，通常（k0<1）随着晶体的生长，熔体中的溶质浓度越来越高，即发生组分过冷的可能性也就逐渐增大了。可能会有这种情况出现，晶体的上半部是好的，而下半部却因组分过冷的出现导致晶体中出现宏观缺陷，甚至变得不透明。过低的生长速率，不仅是不经济的，而且可能使污染和挥发带来的危害变得严重。提高晶体旋转速度，可以促使熔体中溶质均匀化，不过，太高的转速将引起液流的不稳定性，如超过某一临界值Re时，会引起严重的温度振荡。发生界面翻转，这对晶体生长同样也是不利的。加大界面附近熔体中的温度梯度可以有效地抑制组分过冷，然而，高的值就意味着晶体与生长环境之间有较强的热量交换，晶体中将有较大的温度梯度，使晶体中产生较大的热应力，提高了位错密度，严重者可使晶体开裂。高的温度梯度还会增加熔体温度的波动，从而带来有害的瞬时效应。溶质的分凝会带来“灾难性的组分过冷。组分过冷的出现又不是不可避免的，除了有效地控制污染和挥发之外，关键就是如何选择折中的生长参数，即寻找合理的GVω。

3.过冷度与界面稳定性

在进行上述讨论时，我们是假定固液界面上的实际温度就等于凝固点温度，即不考虑过冷度的要求。而实际上，晶体生长的驱动力一定要由过冷度（当然还有过饱和度）来提供，否则晶体是不会长大的。若定义Tm为平衡温度（即凝固点），T为熔体的实际温度，则过冷度为ΔT=Tm-T，如果是ΔT>0，表明界面附近熔体的实际温度低于平衡温度，此时的熔体处于过冷状态；而如果有ΔT<0，表明界面附近熔体的实际温度高于平衡温度，此时的熔体则处于过热状态；如果不存在过冷度，即Tm=T，则此时固液界面处于平衡状态，既不生长也不溶化。

同时，如果ΔT（x）随距界面距离x的增大而增大，即从界面越深入熔体，过冷度就越大，则界面将是不稳定的，因为距离较远的地方有较大的过冷度，该处必然有较大的生长速率；如果熔体中的ΔT（x）是随距界面距离x的增加而减小，即从界面越深入熔体，过冷度就越小，在这种情况下界面将是稳定界面，也不会出现组分过冷。这些内容前边我们已多次提到过。这里需要补充的是，在晶体生长过程中如果界面上Tm和T不相等，界面的行为将如何。图3-11给出了界面附近凝固点Tm和距离x的关系曲线及两种可能的实际温度分布（A和B）。如果熔体中的实际温度分布如B线所示，则从界面起越深入熔体，过冷度（Tm-T）就越大，于是界面越不稳定，即出现组分过冷现象。如果熔体中的实际温度分布如A线所示，则从界面起越深入熔体，过冷度（Tm-T）就越小，因而界面是稳定的，或者说不出现组分过冷。从这里我们不难得出两个结论：首先是在晶体生长过程中，过冷度是必需的，否则就没有生长驱动力，而组分过冷又是必须避免的，因为它将导致胞状界面的产生，严重地影响晶体的品质。对于掺质的材料或非同成分熔化的材料，要得到优质单晶比得到纯材料的单晶要困难一些，其中重要的原因之一也在于此。其次是过冷度本身只影响晶体的生长速率，而不直接破坏界面的稳定性。

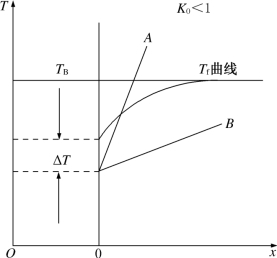
图3-11　界面附近的温度分布