转矩的实用表达式及应用技巧

上述参数表达式，对于分析电磁转矩与电动机参数之间的关系，进行某些理论分析，是非常有用的。但是根据式（7.3.4）绘制机械特性曲线，或将该式用于工程计算，必须知道电动机的参数r1、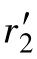、、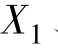等，而这些参数在电动机的产品目录中是查不到的，因此不够实用。为了便于对电力拖动问题进行分析和计算，必须导出电磁转矩的实用表达式。

将式（7.3.4）除以式（7.3.3）得

由式（7.3.5）得到：

故有：

不论S为何值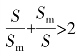，；又Sm 值大致在0.1～0.2之间，因此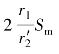比2小得多，为了避免用到参数r1和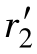，将上式分子分母中的忽略不计，于是得到实用转矩表达式为

式（7.3.9）中的Tm 可从电动机的产品目录中查得的数据求得，计算方法如下：

式中，有：

上两式中的β、PN、nN 均可从产品目录中查得，将S=SN 及T=TN 代入式（7.3.9）得

移项得

即

故有：

式中的“±”号，只有“+”号有实际意义，因为“-”号求得的临界转差率Sm 将小于额定转差率SN，实际上不存在。已知SN及β，可通过上式求得Sm。这样在转矩实用表达式中，只剩下T和S两个未知数。如欲绘制异步电动机的机械特性曲线，只要给定一系列的S值，就能按实用表达式求出相应的T值，即可绘出T=f（S）（或n=f（T））曲线。同样，利用式（7.3.9）还可以进行机械特性的其他计算，其应用极为广泛。但是，运用实用表达式时要特别注意，它只适用额定负载以内的情况，不能推广到S＞Sm 的区域。这是由于在导出这个公式时，作了多次假定与忽略的原因。(www.xing528.com)

前述三相异步电动机电磁转矩的3种表达式，其应用场合各有不同。物理表达式一般适用于定性分析T与Φm 及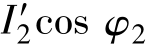之间的关系；参数表达式可用于分析各种参数变化时对电动机运行性能的影响；实用表达式最适用于机械特性的工程计算和机械特性曲线的绘制。实际上转矩表达式可视为异步电动机的机械特性方程式。

【例7.3.1】 一台三相6极笼型异步电动机，PN=3kW，U1N=380V，Y接法，nN=957r/min，r1=2.08Ω，X1=3.12Ω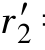，=1.525Ω，=4.25Ω，求该电动机的额定电磁转矩、最大转矩、过载能力、起动转矩及其倍数。

【解】

按Y接法，得额定相电压为

故有：

额定负载转矩为

过载能力为

起动转矩为

起动转矩倍数为

7.3测试题及答案