理解RC电路电容的充电过程

图5.2.4　所示是一个RC 串联电路，换路前电容没有初始储能，即uC（0-）= 0 V。在t=0时，开关S 闭合，这时电源对C 充电。根据KVL 定律，充电时的回路电压方程为

将uR（t）=iC（t）R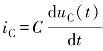，代入上式得

式（5.2.6）是常系数一阶线性非齐次微分方程，其解由特解u′C（t）和通解u″C（t）两部分组成，即

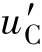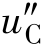式中，特解（t）是满足原微分方程的任意解，通常取电路在时的稳态值作为特解，又称稳态分量；通解（t）是一个随时间变化的指数函数，它只在过渡过程中出现的，又称为暂态分量；A 为积分常数，由换路定律可确定积分常数A；=RC 为电路时间常数。

在t=0+时，由式（5.2.7）得，则有

故，电容电压的全解为

又因为电容充电电压的稳态分量就是电源电压，即；根据换路定则得uC（0+）=uC（0-）= 0，故有

电容的充电电流为(www.xing528.com)

电阻上的电压为

可见，电容充电过程中，其端电压是不能突变的，RC 充电电路中uC（t）、iC（t）的变化曲线都是按指数规律变化的，如图5.2.5 所示。RC 电路充电过程的快慢是由时间常数=RC 来决定的。越小，充电越快；越大，充电越慢，过渡过程需要的时间就越长。RC电路电容充电过程的实质，就是电源提供的能量一部分储存在电容电场中，另一部分被电阻消耗掉。

【例5.2.2】 电路如图5.2.6 所示，US=220 V，R=100 Ω，C=0.5 μF，试求：（1）S闭合后（t=0），电流初始值iC（0+）（uC（0-）= 0）；（2）时间常数；（3）S 接通150 μs 时，电路中电流和电容上电压的数值。

图5.2.4　RC 充电电路

图5.2.5　RC 电路电容充电曲线

图5.2.6　例5.2.2 图

5.2　测试题及答案