航天器状态模型优化方案

最小二乘法估计每次通过处理全部观测数据来改进某一历元的状态量，滤波估计则每次处理一个观测数据并产生每个测量时刻状态矢量的最优估计值。最小二乘法估计轨道确定的基本原理是找到一条轨道和模型参数，使得实际和理论观测值之间的残差平方和最小。而在实际应用中，不同的测量方法，其计量单位和可靠性也不一样，所以每个残差都对应一个权重因子。加权最小二乘法已广泛应用于探测器的初轨确定中，如在“深空1号”“Deep Impact”探测器［122］等自主导航中都应用该方法进行导航滤波。

根据轨道坐标系中航天器两体运动特点，用数学模型重建两体运动。由4.2节理论可知，如果已知矩阵A和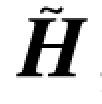，可使用WLS法估计初始轨道状态［123］。

忽略其他惯性力的影响，假设航天器只受中心引力影响。因此，设航天器的状态向量为

式中：（x，y，z）和（u，v，w）分别为某点处航天器的位置矢量和速度矢量。根据二体运动方程，得到

根据式（4-18），得到下式

根据式（4-12），得到

和式（4-7），得到Φ（tj，tk）(www.xing528.com)

式中：Tjk=tj-tk。

根据式（4-12），观测值表示为

也可表示为

式（4-25）可表示为

式中：ε1，…，εi为测量误差引起的理论观测值和实际观测值之差，通常情况下认为服从无偏白噪声分布。

如果矩阵A的特征值和特征向量已知，就可以计算出Φ（t，t0）。实际上，不同类型观测数据的权重可以简单地用其误差的倒数来加权，即用归一化的残差来代替残差。因此，用WLS法来估计航天器的状态矢量，该状态矢量的最佳估计表示为