【摘要】：扩展卡尔曼滤波是将非线性系统的状态方程和观测方程通过一阶泰勒展开近似为线性系统来处理。对于非线性程度高的系统，扩展卡尔曼滤波器存在严重的线性化误差，影响滤波精度。针对该点不足，Juliear和Uhlmann提出无迹卡尔曼滤波算法，该算法不需要计算雅可比矩阵，不需要对状态方程和测量方程线性化，直接通过Sigma点的选取和变换来近似均值与方差，这种变换可获得二阶以上的高精度统计信息。
扩展卡尔曼滤波是将非线性系统的状态方程和观测方程通过一阶泰勒展开近似为线性系统来处理。对于非线性程度高的系统，扩展卡尔曼滤波器存在严重的线性化误差，影响滤波精度。针对该点不足，Juliear和Uhlmann提出无迹卡尔曼滤波算法，该算法不需要计算雅可比矩阵，不需要对状态方程和测量方程线性化，直接通过Sigma点的选取和变换来近似均值与方差，这种变换可获得二阶以上的高精度统计信息。
式中：Xk∈Rn为n×1的状态向量，Yk∈Rm是m×1观测向量，Wk∈Rn为n×1的过程噪声随机向量，Vk∈Rm是m×1测量噪声随机向量。
假设系统的测量噪声和过程噪声为互不相关的高斯白噪声，则其均值为0，协方差矩阵表示为
式中：δi，j是克罗内克δ函数。
UKF算法流程如下［95］：
（1）初始化
（2）构造Sigma采样点和权重(www.xing528.com)
采用比例对称采样策略，构造Sigma点集合｛χ0，k-1|i=0，1，…，2n，k≥1｝为
UKF滤波参数λ=α2（n+k）-n（0≤α≤1），α控制Sigma点的分布状态，调节α可以减小非线性方程的高阶项影响。
（3）时间更新
（4）测量更新
（5）输出结果
输出当前时刻系统状态估计值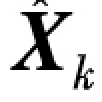
和协方差矩阵Pk后，转到步骤（2）开始新一轮滤波计算。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
