1.测量误差的分类及特性
测量误差按其性质可分为系统误差、随机误差和粗大误差。
1)系统误差:指在相同条件下,多次重复测量同一量时,其误差的大小和符号保持不变或按一定规律变化的误差。前者称为定值系统误差,后者称为变值系统误差。例如,用千分尺测量零件时,千分尺零位调整不正确对各次测量结果的影响是相同的。因此引起的测量误差为定值系统误差。又如指示表的刻度盘与指针回转轴偏心所引起的按正弦规律周期变化的测量误差,属于变值系统误差。
2)随机误差:指在相同条件下,多次测量同一量值时,其误差的大小和符号以不可预见的方式变化的误差。随机误差是测量过程中许多独立的、微小的、随机的因素引起的综合结果。如计量器具中机构的间隙、运动件间的摩擦力变化、测量力的不恒定和测量温度、湿度的波动等引起的测量误差都属于随机误差。在同一测量条件下,重复进行的多次测量中,不可避免会产生随机误差,随机误差既不能用实验方法消除,也不能修正。就某一次具体测量而言,随机误差的大小和符号是没有规律的,但对同一被测量进行连续多次重复测量而得到一系列测得值(简称测量列)时,它们的随机误差的总体存在着一定的规律性。大量实验表明,随机误差通常服从正态分布规律。因此,可以利用概率论和数理统计的一些方法来掌握随机误差的分布特性,估算误差范围,对测量结果进行处理。
(1)随机误差的分布规律及特性。
设用立式光学计对同一零件的某一部位用同一方法进行150次重复测量,然后将150个测得值按尺寸大小分组列入表2-4中。从7.131~7.141mm每隔0.001mm为一组,共分11组。每组尺寸范围如表中第二列所示。每组出现次数ni(频数)列于表第四列。若零件总的测量次数用N表示,则可算出各组的相对出现次数ni/N(频率),见表第五列。将这些数据画成图表,横坐标表示测得值Xi,纵坐标表示出现的频率ni/N,得到图2-11(a)所示的图形,称频率直方图。连接每个小方图的上部中点得到一折线,称为实际分布曲线,如果测量次数足够多且分组足够细,则会得到一条光滑曲线,即正态分布曲线,如图2-11(b)所示。从大量实际分布曲线中,可看出多数随机误差的统计规律。
随机误差通常服从正态分布规律,具有如下四个基本特性:
① 单峰性绝对值小的误差比绝对值大的误差出现的次数多。
② 对称性绝对值相等,符号相反的误差出现的次数大致相等。
③ 有界性在一定测量条件下,随机误差绝对值不会超过一定的界限。
④抵偿性对同一量在同一条件下进行重复测量,其随机误差的算术平均值随测量次数的增加而趋于零。
表2-4 测得值的分布
图2-11 频率直方图和正态分布曲线
(2)随机误差的评定指标。
由概率论可知,正态分布曲线可用其分布密度进行描述,即
式中 y——随机误差的概率分布密度;
χ——随机变量;
x0——数学期望(作为真值);
δ——随机误差;
σ——标准偏差;
e——自然对数的底(e=2.71828)。
从上式可以看出,概率密度y与随机误差δ及标准偏差σ有关,当δ=0时,y最大,即ymax=![]() 。不同的σ对应不同形状的正态分布曲线,σ越小,ymax值越大,曲线越陡,随机误差分布越集中,即测得值分布越集中,测量的精密度越高。反之,σ越大,曲线越平坦,随机误差分布越分散,即测得值分布越分散,测量的精密度越低,如图2-12所示。图中σ1<σ2<σ3,而y1max>y2max>y3max。
。不同的σ对应不同形状的正态分布曲线,σ越小,ymax值越大,曲线越陡,随机误差分布越集中,即测得值分布越集中,测量的精密度越高。反之,σ越大,曲线越平坦,随机误差分布越分散,即测得值分布越分散,测量的精密度越低,如图2-12所示。图中σ1<σ2<σ3,而y1max>y2max>y3max。
根据误差理论,随机误差的标准偏差σ的数学表达式为
图2-12 标准偏差对随机差
式中 n——测量次数;
δi——随机误差,即各次测得值与其真值之差。
(3)随机误差的极限值。
由随机误差的有界性可知,随机误差不会超出某一范围。随机误差的极限值是指测量极限误差,也就是测量误差可能出现的极限值。
若把整个误差曲线下包围的面积看做是所有随机误差出现的概率之和P,便可得到下式:
研究随机误差出现在正、负无穷大区间的概率是没有实际意义的。在计量工作实践中,要研究的是随机误差出现在±δ范围内的概率P,于是便有
将上式进行变量置换,设t=δ/σ,则有
将其代入上式可得
又写成如下形式
P=2Φ(t)
Φ(t)称为拉普拉斯函数,也称概率积分。只要给出t值便可算出概率。不同的t值对应的概率可从有关手册中查得,为了使用方便,表2-5列出了四个不同t值对应的概率。
表2-5 四个不同t值对应的概率
从表2-5中t与概率的数值关系上可以发现,随着t的增大,概率并没有明显的增大。当t=3时,随机误差δ在±3σ范围内的概率为99.73%,超出±3σ的概率只有0.27%。可以近似地认为超出±3σ的可能性为零。
因此,在估计测量结果的随机误差时,往往把±3σ作为随机误差的极限值,即测量极限误差为
称t为误差估计的置信系数,把t对应的概率称为置信概率。按δlim=±3σ式估计随机误差的意义是:测量结果中包含的随机误差不超出δlim=±3σ的可信赖程度达到99.73%。
简单地说就是,标准偏差σ确定后,在δ/σ一定时,利用正态分布曲线,求随机误差的概率。
δ=±σ P=68.26%
δ=±2σ P=95.44%
δ=±3σ P=99.73%
3)粗大误差:指明显超出规定条件下预期的误差。它明显地歪曲了测量结果。粗大误差是由主观和客观原因造成的,主观原因如测量人员疏忽造成读数误差和记录误差。客观原因如外界突然振动引起的误差等。
对系统误差应设法消除或减小其对测量结果的影响;对随机误差需经计算确定其对测量结果的影响;对粗大误差应剔除。
2.测量结果的数据处理
对测量结果进行处理是为了找出被测量最可信的数值以及评定这一数值所包含的误差。在相同的测量条件下,对同一被测量进行连续测量,得到一测量列。测量列中可能同时存在系统误差、随机误差和粗大误差,因此必须对这些误差进行处理。
1)系统误差的发现和消除。
系统误差一般通过标定的方法获得。从数据处理的角度出发,发现系统误差的方法有多种,直观的方法是“残差观察法”,即根据测量值的残余误差,列表或作图进行观察。若残差大体正负相同,无显著变化规律,则可认为不存在系统误差;若残差有规律地递增或递减,则存在线性系统误差;若残差有规律地逐渐由负变正或由正变负,则存在周期性系统误差。当然这种方法不能发现定值系统误差。
发现系统误差后需采取措施加以消除。若已知测量结果(即未修正的结果)中包含的系统误差大小和符号,则可用测量结果减去已知的系统误差值,从而获得不含(或少含)系统误差的测量结果(已修正结果)。也可将已知系统误差取相反的符号,变为修正值,并用代数法将此修正值与未修正测量结果相加,从而计算出已修正的结果。
用简式表示为
测量结果=读数-修正值(初始值)(https://www.xing528.com)
还可以用两次读数方法消除系统误差等。例如,测量螺纹参数时,可以分别测出左右牙面螺距,然后取平均值,则可减小安装不正确引起的系统误差。
2)测量列随机误差的处理。
为了正确地评定随机误差,在测量次数有限的情况下,必须对测量列进行统计处理。
(1)测量列的算术平均值 :在评定有限测量次数测量列的随机误差时,必须获得真值,但真值是不知道的,因此,只能从测量列中找到一个接近真值的数加以代替,这就是测量列的算术平均值。
:在评定有限测量次数测量列的随机误差时,必须获得真值,但真值是不知道的,因此,只能从测量列中找到一个接近真值的数加以代替,这就是测量列的算术平均值。
在同一条件下,对同一个量进行多次(n)重复测量,由于测量误差的影响,将得到一系列不同的测得值x1,x2,…,xn,这些量的算术平均值为
如果在消除了系统误差的前提下,对某一量进行无数次等精度测量,所有测得值的算术平均值就等于真值。
证明如下:由δ=χ-χ0得 δ1=χ1-x0
δ2=χ2-x0
…
δn=χn-x0
各式相加得
由随机误差特性(抵偿性)可知,当n→∞时,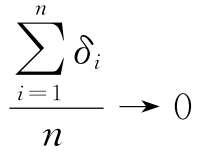 ,所以
,所以
事实上,做无数次测量是不可能的,在进行有限次测量,仍可证明各次测得值的算术平均值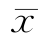 最接近真值x0。所以,当测量列中没有系统误差和粗大误差时,一般取全部测得值的算术平均值
最接近真值x0。所以,当测量列中没有系统误差和粗大误差时,一般取全部测得值的算术平均值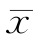 作为测量结果。
作为测量结果。
(2)残差及其应用。
残差是指测量列中的一个测得值xi和该测量列的算术平均值 之差,记作νi。
之差,记作νi。
由符合正态分布规律的随机误差的分布特性可知残差具有两个特性:
① 残差的代数和等于零,即![]() =0。
=0。
② 残差的平方和为最小,即![]() =min。
=min。
实际应用中,常用![]() =0来验证数据处理中求得的
=0来验证数据处理中求得的 与νi是否正确。
与νi是否正确。
对于有限测量次数的测量列,由于真值未知,所以其随机误差δi也是未知的,为了方便评定随机误差,在实际应用中,常用残差νi代替δi计算总体标准偏差,此时所得之值称为总体标准偏差σ的估计值。用下式表示为
总体标准偏差σ的估计值S称为实验标准偏差,简称标准差。当将一列n次测量作为总体取样时,可用S代替评定总体标准偏差。
由式(2-7)估算出S后,便可取±3S代替作为单次测量的极限误差。即
③测量列算术平均值的标准偏差σ 。
。
如前所述,当重复测量次数n→∞时,测得值的算术平均值 比任何一个测得值xi都接近真值x0。但实际测量的次数总是有限的,算术平均值本身也是一个随机变量,且都围绕着真值变动,但重复测量的算术平均值的变动范围比单次测得值的变动范围小,有理由认为重复测量的算术平均值精度比单次测量的精度高。因此,其精度指标也要用相应的算术平均值的标准偏差σ
比任何一个测得值xi都接近真值x0。但实际测量的次数总是有限的,算术平均值本身也是一个随机变量,且都围绕着真值变动,但重复测量的算术平均值的变动范围比单次测得值的变动范围小,有理由认为重复测量的算术平均值精度比单次测量的精度高。因此,其精度指标也要用相应的算术平均值的标准偏差σ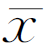 来表示。
来表示。
σ表示测量列中单次测得值xi对真值x0的分散程度。σ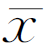 表示平均值
表示平均值 对真值x0的分散程度。根据误差理论,算术平均值的标准偏差σ
对真值x0的分散程度。根据误差理论,算术平均值的标准偏差σ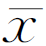 与测量列中单次测量的标准偏差σ有如下关系(公式推导略):
与测量列中单次测量的标准偏差σ有如下关系(公式推导略):
式中 n——每组的测量次数。
由式(2-11)可知,增加测量次数,算术平均值的标准偏差σ 将减小,即测量精度可提高。但当S一定时,n>10以后,σ
将减小,即测量精度可提高。但当S一定时,n>10以后,σ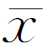 减小缓慢,故在实际生产中,一般情况下取n≤10。
减小缓慢,故在实际生产中,一般情况下取n≤10。
测量列算术平均值的测量极限误差可表示为
测量列的测量结果可表示为
这时的置信概率:P=99.73%。
3)粗大误差的处理。
粗大误差的特点是数值比较大,对测量结果产生明显的歪曲,对它的处理原则是:按一定规则从测量数据中将其剔除。判断粗大误差常用拉依达准则,又称3σ准则。
当测量列服从正态分布时,在±3σ外的残差的概率仅有0.27%,即在连续370次测量中只有一次测量的残差超出±3σ(370×0.0027≈1),而实际上连续测量的次数绝不会超过370次,测量列中就不应该有超过±3σ的残差。因此,在有限次测量时,凡残余误差超过3S时,即
│νi│ >3S
则认为该残差对应的测得值含粗大误差,应予以剔除。
当测量次数小于或等于10次时,不能使用拉依达准则。
例2-2 用立式光学计对一个直径为![]() 的轴,在某一截面上做等精度测量,重复测量10次,测得值χi列于下表中;假设系统误差已消除,粗大误差已剔除,试确定测量结果。
的轴,在某一截面上做等精度测量,重复测量10次,测得值χi列于下表中;假设系统误差已消除,粗大误差已剔除,试确定测量结果。
解:(1)计算测量列的算术平均值 。
。
所以轴的直径可靠值为φ24.9997mm。
(2)列表计算残差ν。
(3)计算测量列单次测量的标准偏差σ。
(4)计算算术平均值的标准偏差σ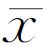 。
。
(5)测量列单次测量的极限误差δlim。
δlim=±3σ=±3S=±3×0.21=±0.63μm≈±0.0006mm
(6)测量列算术平均值的极限误差δlim(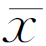 )。
)。
δlim( )=±3σ
)=±3σ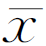 =±3×0.0664=±0.199μm≈±0.0002mm
=±3×0.0664=±0.199μm≈±0.0002mm
(7)测量结果。
①用平均值表示:χ=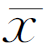 ±3σ
±3σ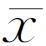 =24.9997±0.0002mm
=24.9997±0.0002mm
② 还可用单次测得值表示(如第7次测得值):χ′7=24.9996±0.0006mm
24.9997(24.9996)是测量结果,±0.0002(±0.0006)是随机误差可能存在的范围。比较两式可以看出,单次测量结果的误差大,测量可靠性差;因此,精密测量中常用重复测量的测得值的算术平均值作为测量结果,用算术平均值的标准偏差或算术平均值的极限误差评定算术平均值的精密度。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




