层次分析法在决策中的应用

（1）枢纽布置备选方案。枢纽布置3种方案，包括原可行性阶段枢纽布置方案、溢洪道右移优化方案、溢洪道右移及过坝道路后移优化方案，分别记为方案P1、P2、P3。

（2）AHP模型建立。确定目标层、准则层：为了研究方便，利用“枢纽布置设计满意度指标R”作为研究的目标层。经咨询专家和分析调研，得出当前评价枢纽布置设计满意度指标R的主要因素，确定R由6个指标组成（见表4.6）。

表4.6　枢纽布置设计满意度指标R的6个指标表

（3）构造判断矩阵。根据各项指标之间的重要性关系，并参照表4.4构造判断矩阵（见表4.7），满意度6个指标的判断矩阵（见表4.8）。

表4.7　目标层判断矩阵表

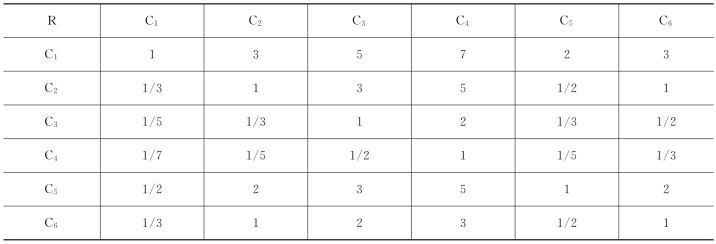
表4.8　布置优化6个评价指标判断矩阵表

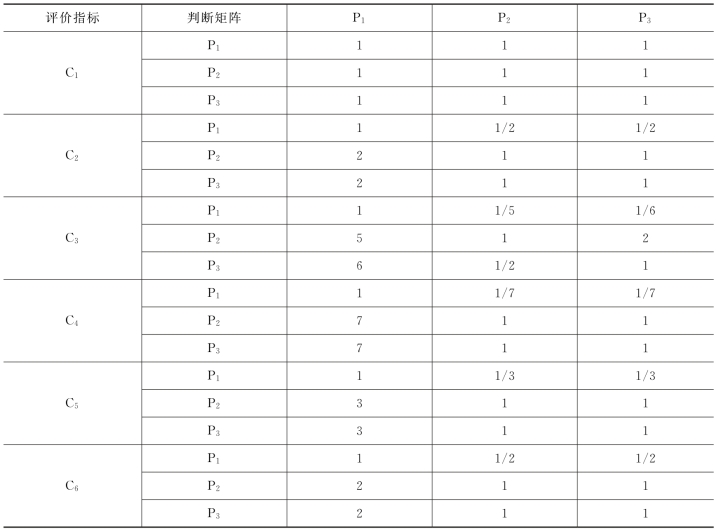
（4）采用和法计算特征向量及一致性检验。

1）目标层级评价指标判断矩阵特征向量及一致性检验。目标层级评价指标判断矩阵，见表4.7。

A.首先计算各列元素总和，目标层判断矩阵各列总和值见表4.9。

表4.9　目标层判断矩阵各列总和值

B.然后每一元素除以其列的总和值并计算每行的平均值（见表4.10）。

表4.10　目标层判断矩阵元素各列总和的商和每行平均值

由表4.10中，则称［0.3783，0.1546，0.0695，0.0414，0.2496，0.1286］为目标判断矩阵的特征向量。

C.进行一致性检验。先把目标判断矩阵元素乘以相应的特征向量（权重）（见表4.11）。

表4.11　目标层判断矩阵元素特征向量的积与每行的和值

由每行均值除以对应的每行和值则：2.3644/0.3873=6.1048，0.9496/0.1546=6.1423，0.4270/0.0695=6.1439，0.2539/0.0414=6.1329，1.4207/0.2496=5.6919，0.7973/0.1286=6.1998。

计算其平均值：λ=1/n∑（Aw）i/wi

λ=（6.1048+6.1423+6.1439+6.1329+5.6919+6.1998）/6=6.0693

一致性指标：CI=CI=（λmax-n）/（n-1）=（6.0693-6）/（6-1）=0.0139

一致性率：CR=CI/RI=0.0139/1.24=0.0112（n为6时，查表4.5得RI为1.24）

CR=0.0112＜0.10

可见，目标层级判断矩阵具有满意一致性。

2）准则层级指标判断矩阵特征向量及一致性检验。新老3个方案在枢纽布置设计满意度6个指标的判断矩阵见表4.8。

A.首先分别计算C1、C2、C3、C4、C5、C6各判断矩阵的各列元素总和（见表4.12）。

表4.12　满意度指标的判断矩阵各列总和值

B.然后每一元素除以其列的总和并计算每行的平均值（见表4.13）。(www.xing528.com)

表4.13　满意度指标判断矩阵元素各列总和的商和每行平均值

由表4.13中，则称［0.3333，0.3333，0.3333］、［0.2000，0.4000，0.4000］、［0.0819，0.3430，0.5750］、［0.0667，0.4667，0.4667］、［0.1429，0.4286，0.4286］、［0.2000，0.4000，0.4000］分别为准则层级单一指标C1、C2、C3、C4、C5、C6判断矩阵的特征向量。

C.进行一致性检验。先把目标判断矩阵的元素乘以相应的特征向量（权重）（见表4.14）。

表4.14　满意度指标判断矩阵元素特征向量的积与每行的和值

续表

则：1.0000/0.3333=3，1.0000/0.3333=3，1.0000/0.3333=3；

0.6000/0.2000=3，1.2000/0.4000=3，1.2500/0.4000=3；

0.2463/0.0819=3.0073，1.0400/0.3430=3.0321，1.7524/0.5750=3.0477；

0.2001/0.0667=3，1.4001/0.4667=3，1.4001/0.4667=3；

0.4286/0.1429=3，1.2858/0.4286=3，1.2858/0.4286=3；

0.6000/0.2000=3，1.2000/0.4000=3，1.2000/0.4000=3。

计算其平均值：λ=1/n∑（Aw）i/wi

λ1=（3+3+3）/3=3；

λ2=（3+3+3）/3=3；

λ3=（3.0073+3.0320+3.0477）/3=3.0290；

λ4=（3+3+3）/3=3；

λ5=（3+3+3）/3=3；

λ6=（3+3+3）/3=3；

一致性指标：CI=CI=（λmax-n）/（n-1）=（3.0290-3）/（3-1）=0.0145

一致性率：CR=CI/RI=0.0145/0.58=0.0250（n为3时，查表4.5得RI为0.58）

CR=0.0250＜0.10，可见，准则层级判断矩阵具有满意一致性。

3）层次总排序。通过进行特征向量求解，已经得到6个评价指标的特征向量，以及每个单一评价指标下的3个方案的特征向量（见表4.15）。

各方案总得分：

表4.15　特征向量表

P1：0.3783×0.3333+0.1546×0.2000+0.0695×0.0819+0.0414×0.0667+0.2496×0.1429+0.1286×0.2000=0.2268

P2：0.3783×0.3333+0.1546×0.4000+0.0695×0.3430+0.0414×0.4667+0.2496×0.4286+0.1286×0.4000=0.3895

P3：0.3783×0.3333+0.1546×0.4000+0.0695×0.5750+0.0414×0.4667+0.2496×0.4286+0.1286×0.4000=0.4056

由此可知，方案P3的权值为0.4056，其值最大，在层次总排序中重要性程度高于方案P1、P2，为最优方案。

层次分析法能对评价方案的各因素提供其重要性权值的综合排序，有利于设计人员抓住影响工程设计的各种重要因素。在枢纽布置方案优化选择上，层次分析法为其提供了科学的依据，能够使以往的定性分析变为定量分析，克服了以往单靠实践经验的盲目性，分析结果一目了然。它不仅是定量确定各评价指标相对重要性的有效手段，而且对于方案本身所包含的各因素的综合定量分析也是行之有效的，是一个科学有效的方法，可以应用于众多其他行业的方案比选中。