层次分析法(Analytic Hierarchy Process,简称AHP法)是美国运筹学家T.L.Sattg等人创立的一种定性分析和定量分析有机结合的系统分析、决策新方法。它是一种以递阶层次结构模型求得每一个具体目标的权重,进而解决多目标决策的非数学模型优化方法。该方法把一个复杂的问题表示成递阶层次结构模型,利用预选方案的优劣程度进行判断排序,从而得出最优方案,为设计提供依据。
运用AHP方法,大体可分为以下4个步骤:①建立层次结构模型,将有关因素按不同属性自上而下地分解成若干层次,同一层诸因素从属于上一层因素或对上层因素有影响,同时又支配下一层的因素或受到下层因素的作用。②分析系统中各因素间的关系,对同一层次各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较的判断矩阵;③由判断矩阵计算被比较元素对于该准则的相对权重,并进行判断矩阵的一致性检验;④计算各层次对于系统的总排序权重,并进行排序。最后,得到各方案对于总目标的总排序。
(1)建立层次结构模型。根据问题性质和决策目标把问题中包含的因素划分为不同的层次,形成一个多层次的分析结构模型。首先,把复杂的问题分解为各种指标,再把这些指标按照不同性质分成若干组,以形成不同的层次。同一层次上的指标作为准则,对下一层次的某些指标起支配作用,同时它又受上一个指标的支配。处于最上层的指标一般只有一个,称为目标层,一般就是分析问题的预定目标或理想结果。中间层次一般是准则层或子准则层。
(2)构造判断矩阵。根据表4.4所示1~9标度法,逐项就任意2个评价指标进行比较,确定它们的相对重要性程度赋以相应的分值,进而构造判断矩阵。
表4.4 比较尺度表(1~9尺度的含义)

(3)各因素权重求解。对判断矩阵求解各因素权重,其常用方法有规范列平均法、方根法、幂乘法等。
规范列平均法的步骤如下:
第一步,先求出两两比较矩阵的每一元素每一列的总和。
第二步,把两两比较矩阵的每一个元素除以其相对应列的总和,所得的商称为标准两两比较矩阵。
第三步,计算标准两两比较矩阵的每一行的平均值,这些平均值就是各方案在某一评价指标方面(比较因素)的权重,也即方案优化评价中的特征向量。
第四步,求得其他评价指标在方案优化评价中的特征向量。
第五步,把所有评价指标的特征向量列成矩阵表。
第六步,取得每个评价指标在总目标中的相对权重,即要取得每个评价指标的相对权重。即评价指标的特征向量。
第七步,通过两两比较矩阵,同样求出其评价指标的特征向量值。
(4)一致性检验。判断矩阵A=(aij)n×n,其具有如下性质:

从理论上分析得到:如果A是完全一致的成对比较矩阵,则其应该具有传递性质:
![]()
即判断矩阵具有完全一致性。但实际上在构造成对比较矩阵时要求满足上述众多等式是不可能的,因此退而要求成对比较矩阵有一定的一致性,即可以允许成对比较矩阵存在一定程度的不一致性。由分析可知,对完全一致的成对比较矩阵,其绝对值最大的特征值等于该矩阵的维数。对成对比较矩阵的一致性要求,转化为要求其绝对值最大的特征值和该矩阵的维数相差不大。
检验成对比较矩阵的一致性检验方法如下:
计算衡量一个成对比较矩阵A(n>1阶方阵)不一致程度的指标CI:
![]()
当λmax=n,CI=0时,为完全一致情况;CI值越大,判断矩阵的完全一致性越差。在计算判断矩阵时,为了度量不同阶判断矩阵是否完全一致性,引入判断矩阵的平均随机一致性指标RI。RI是这样得到的:对于固定的n,随机构造成对比较矩阵A,其中aij是从1,2,…,9,1/2,1/3,…,1/9中随机抽取的。这样的A是不一致的,取充分大的子样得到A的最大特征值的平均值。从有关资料查出检验成对比较矩阵A一致性的标准RI,它为同阶矩阵的一致性指标的随机均值,其RI值见表4.5。
表4.5 平均随机一致性指标RI值

注 n为矩阵阶数,它只与矩阵阶数n有关。
随机一致性比率CR为一致性指标CI与同阶平均随机一致性指标RI的比值,即CR=CI/RI。当CR<0.10时,认为判断矩阵通过了一致性检验,具有满意的一致性,否则应对判断矩阵进行调整,使其最终满足要求。
检验一致性的步骤如下:
第一步,由被检验的两两比较矩阵乘以其特征向量,所得的向量赋权和向量。(https://www.xing528.com)
第二步,每个赋权和向量的分量分别除以对应的特征向量的分量,即第i个赋权和向量的分量除以第i个特征向量的分量。
第三步,计算出每个结果中的平均值,记为λmax。
第四步,计算一致性指标CI。
第五步,计算一致性率CR,其中RI从表4.5中选取。
第六步,根据是否满足CR≤0.10来判断比较矩阵的一致性。
第七步,同样,可以通过计算其他评价指标一致性率CR,来判断其一致性,即相应的特征向量有效。
(5)利用特征向量求出各方案的优劣次序。
根据求出的评价指标的特征向量,以及评价指标下每个方案的特征向量求出各方案的总得分。通过比较各方案的得分多少,找到最优方案及不同方案的优劣次序。
(6)特征向量计算方法。在AHP方法中,用定义计算两两比较矩阵的特征值和特征向量相当困难,特别是阶数较高时。
两两比较矩阵是通过定性比较得到的比较粗糙的结果,对它的精确计算也没有太大的必要。故用近似计算即可满足要求,主要有和法、根法、幂法等。和法(规范列平均法)是计算判断矩阵A各列各个元素ai的和;将ai的各列元素的和进行归一化,该向量即为所求权重向量。根法(几何平均法)是计算判断矩阵A各行各个元素ai的乘积;计算ai的n次方根;对向量进行归一化处理,该向量即为所求权重向量。
1)定理:对于正矩阵A(A的所有元素为正)
A.A的最大特征根为正单根λ;
B.λ对应正特征向量w(w的所有分量为正);
C.w=lim(Ak e/eT Ak e),其中e=(1,1,…,1)T,w是对应λ的归一化特征向量。
2)和法的计算步骤如下:
A.将A的每一列向量归一化得 ij=aij/∑aij;
ij=aij/∑aij;
B.对 ij按行求和得
ij按行求和得 i=∑
i=∑ ij;
ij;
C.归一化 =(
=( 1,
1,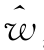 2,…,
2,…, n)T;
n)T;
wi= i/∑
i/∑ iw=(w1,w2,…,wn)T;
iw=(w1,w2,…,wn)T;
D.计算Aw;
E.计算λ=1/n∑(Aw)i/wi,最大特征值的近似值。
3)根法的计算步骤如下:
A.将A的每一列向量归一化得 ij=aij/∑aij;
ij=aij/∑aij;
B.对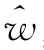 ij按行求积得
ij按行求积得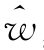 i=(∏
i=(∏ ij)1/n;
ij)1/n;
C.归一化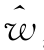 =(
=( 1,
1,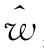 2,…,
2,…, n)T
n)T
wi= i/∑
i/∑ iw=(w1,w2,…,wn)T;
iw=(w1,w2,…,wn)T;
D.计算Aw;
E.计算λ=1/n∑(Aw)i/wi,最大特征值的近似值。
以上方法中和法最为简便。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




