根据所得的五个当地线性模型，当利用直接法辨识时可利用图10-45中模型框架求取插值函数即可得到全局LPV模型，此时各当地线性模型的输出估计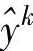
可直接利用全局系统输入u（t）通过传递函数
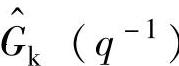获得；而若需要采用基于闭环的方法，即通过激励信号产生各当地线性模型的输出估计
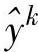，则需左上角进行调整，最终的结构框架如图所示。此时若先获得闭环对象LPV模型，则需代入控制器结构换算开环对象模型，即
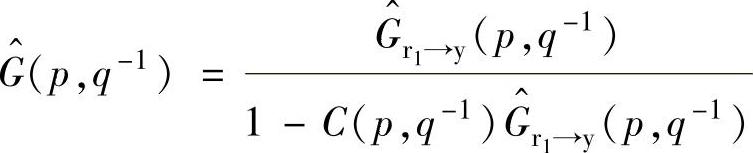
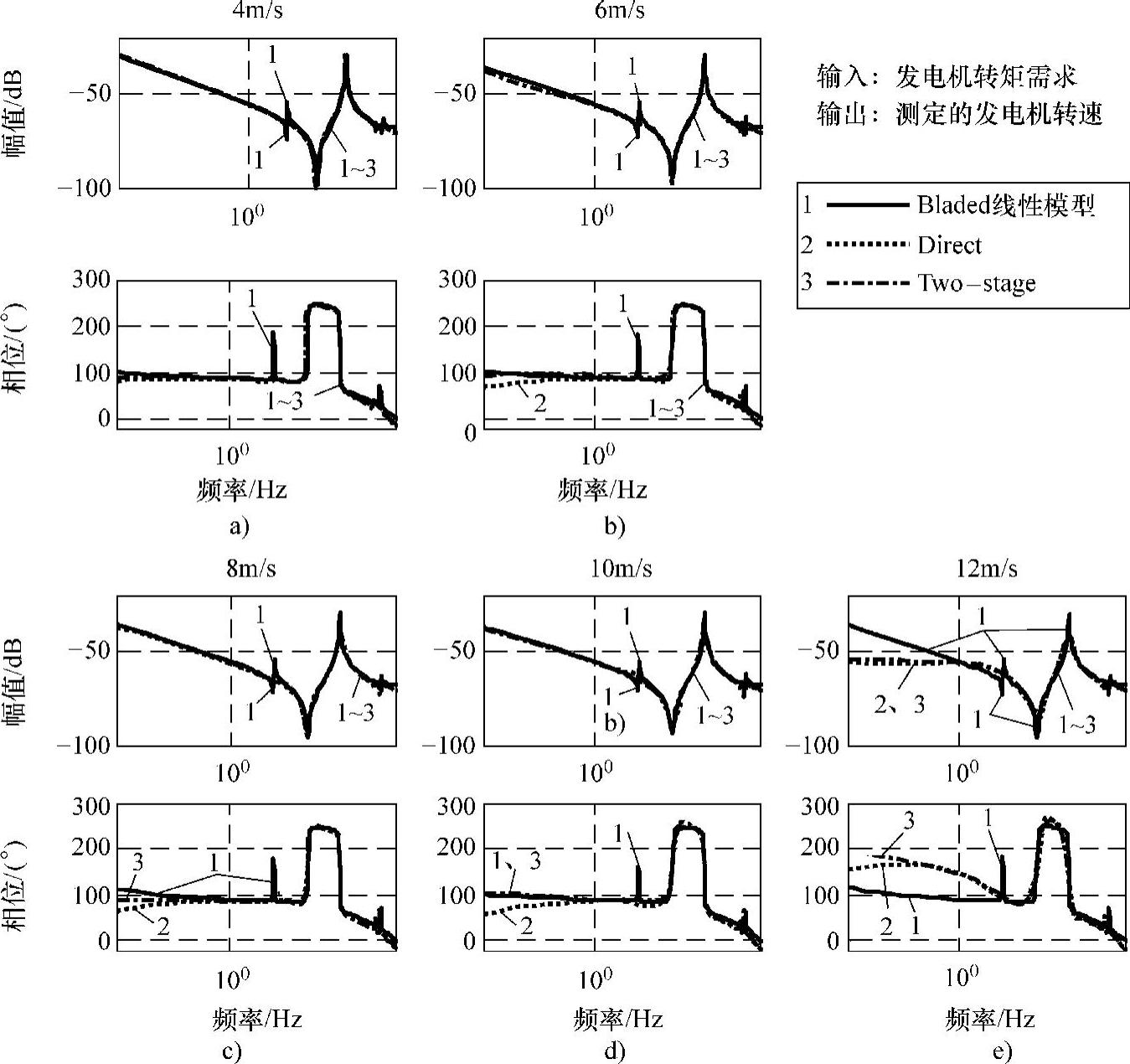
图10-44 当地线性模型辨识结果
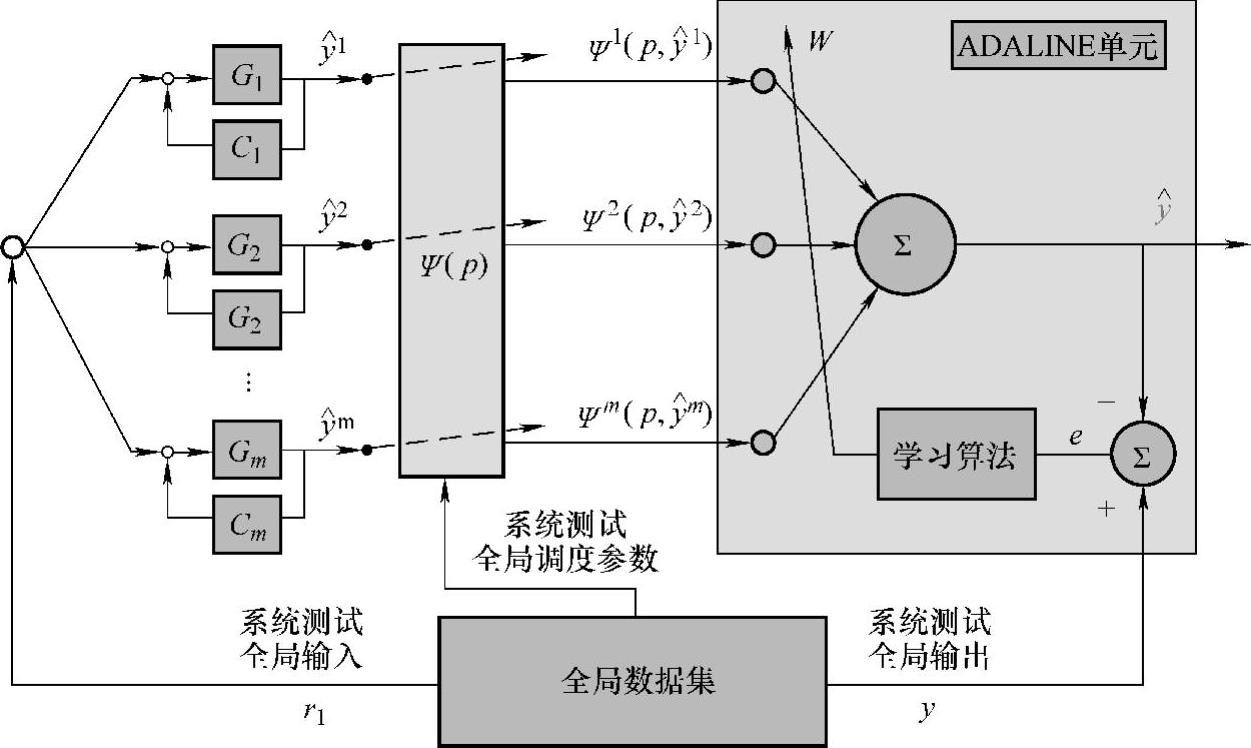
图10-45 基于ADALINE方法的闭环对象全局LPV模型辨识框架
基于此五个工作点建立起的全局LPV模型结果如图10-46所示。需要注意的是，此时图b、c的伯德图比较中，点画线所表示的辨识当地模型，为对系统进行该工作点下独立的激励试验，并收集所得数据辨识所得的结果。此时，从伯德图比较来看，高频段由于各个当地模型比较接近，能够取得较好的辨识结果；而在1Hz频率附近以下，LPV模型会有相频特性和幅频特性的偏差；尤其在相频特性曲线上，LPV模型表现出一个明显的凸起。一方面这是由于12m/s的工作点附近的模型辨识不精确，导致使用该当地线性模型进行插值获得的LPV全局模型不精确（模型权重带来的偏差）；一方面当系统变量如增益或时间常数等随着调度参数变化呈现单调特性时，LPV模型会有较好的近似，不论期望发电机转矩曲线还是变化测量发电机转速曲线，当风速从10m/s跨度到12m/s过程中均呈现异常的变化趋势，表明风电机组已经进入过渡阶段。
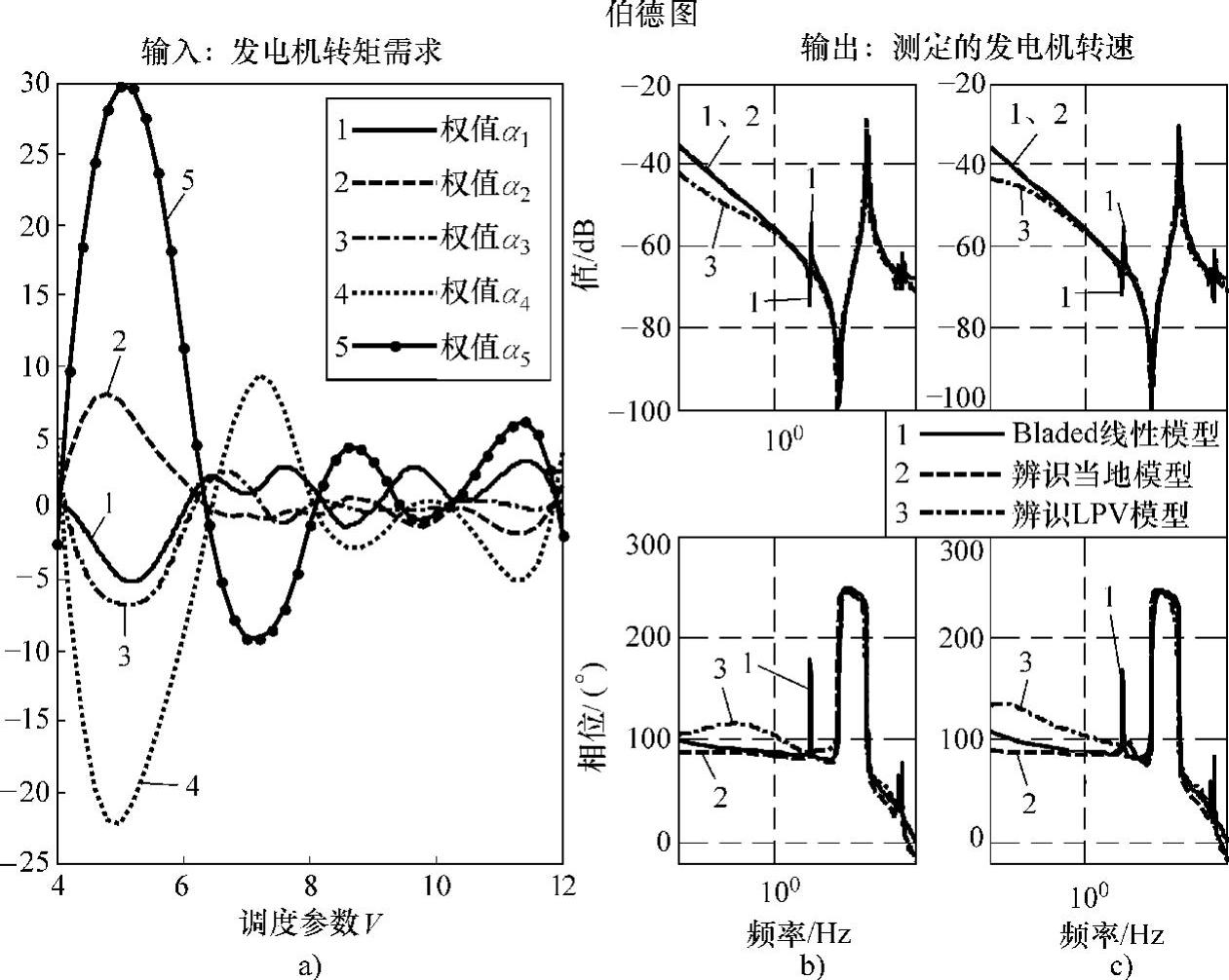
图10-46 LPV模型辨识结果（5个风速工作点：4m/s、6m/s、8m/s、10m/s、12m/s）
a）插值函数 b）伯德图（5m/s） c）伯德图（9m/s）
根据前述两点分析，不妨剔除12m/s的工作点，将LPV模型压缩至4～10m/s区域范围内，即风速工作点设置只有4m/s、6m/s、8m/s、10m/s这4个，重新辨识4～10m/s全局LPV模型（结果如图10-47所示）。此时，图a的插值函数曲线来看，比采用5个工作点时压缩到了一个较小的变化范围内。当然，从插值函数并不能判断模型的精准性。为验证模型的有效性，同样地绘制LPV模型在风速5m/s和9m/s情形下的伯德图比较，如图b、c所示。此时，比对图b、c中情形，可以看到模型的性能要有一定的改善；图b中，低频段特性的凸起特性虽然没有消除，但是偏差值已经被削弱；而图c中，LPV模型的突起已经被消除，其低频段特性辨识当地模型基本一致。当然，如果要得到更好的LPV模型性能，可将系统工作域划分为更加精细的工作子域，再分别采用LPV方法建立各子域模型，综合各子域模型得到全局LPV模型。此时，针对任一风速点如5.5m/s，只需利用该风速点的插值函数和4个当地线性模型即可求取其风速点模型。如此，我们即建立好4～10m/s全局范围内任意风速工作点下的模型，弥补了非整数工作点风速下的模型在Bladed线性模型中无法获取的不足。(www.xing528.com)
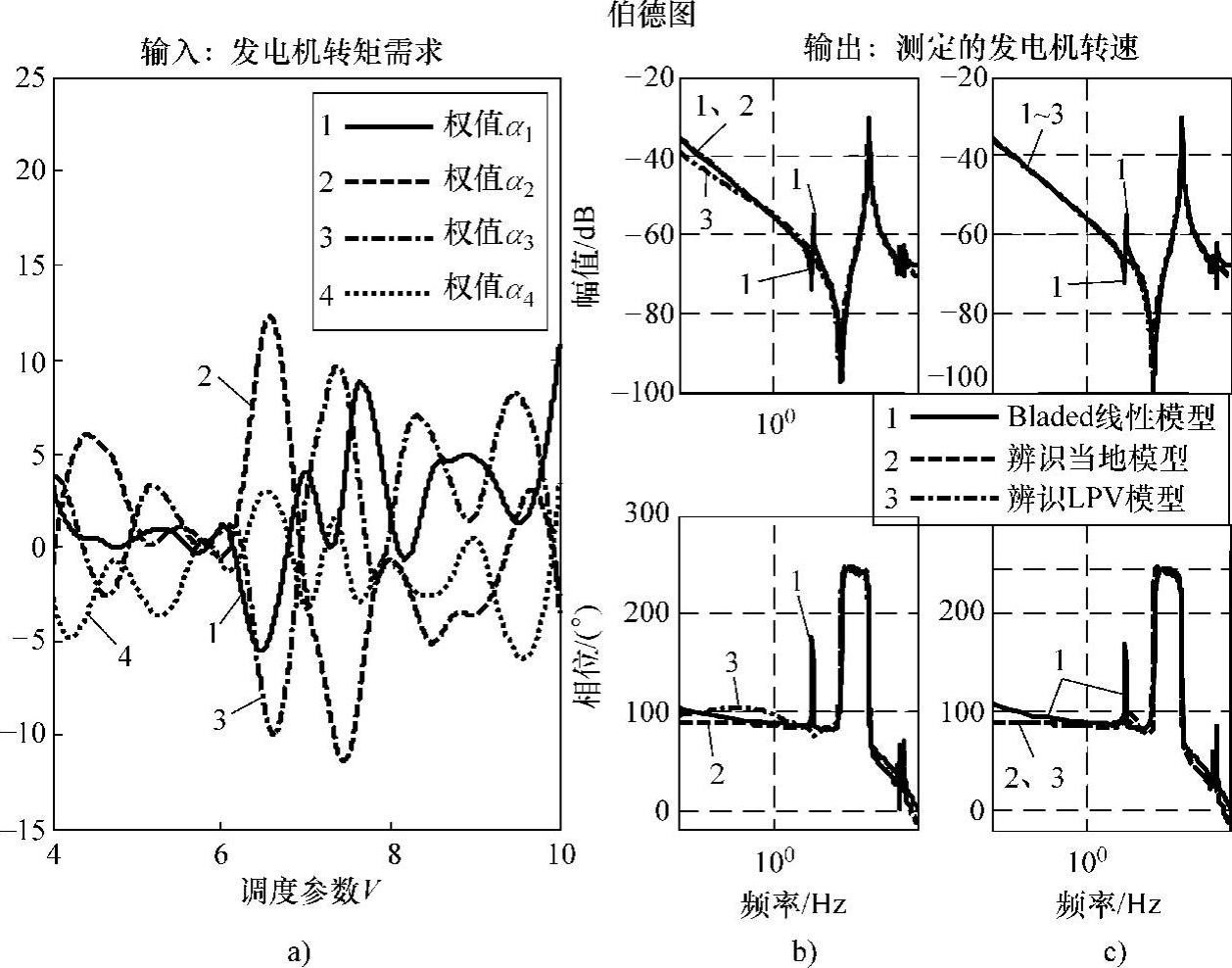
图10-47 LPV模型辨识结果（4个风速工作点：4m/s、6m/s、8m/s、10m/s）
a）插值函数 b）伯德图（5m/s） c）伯德图（9m/s）
将上述方法应用于桨距控制环LPV模型建立，取风速工作点为12m/s、14m/s、16m/s、18m/s、20m/s、22m/s、24m/s，进行激励测试后获取各工作点当地线性模型，结果如图10-48所示。此时可以看到在22m/s、24m/s时，由于系统已经邻近机组停机边缘，激励信号叠加后的开环对象输入由于受基于安全性、可靠性而设置的诸多限幅环节等影响，采用线性模型辨识效果较差；同时在12m/s附近也因为邻近过渡区域，其幅值上的辨识效果也比其他工作点呈现一定差异。因此，不妨剔除上述工作点，采用14～20m/s区域进行LPV模型建立。此时，对应的结果如图10-49所示。此时，图a的插值函数变化范围也较窄，与前述转矩环特性类似，这应该是4个工作点时的插值函数变化特性；而图b、c分别为15m/s和17m/s情形下的伯德图比较结果，同样辨识当地模型为独立试验所辨识得到的模型。从伯德图比较来看，LPV模型的幅频特性能够有较好的性能，其与辨识当地模型只有在波谷处的微小差别；但三者模型的相频特性相差较大，这与各个当地线性模型的相位估计相差较大有关，在实际应用中应当针对具体情况进行校正。
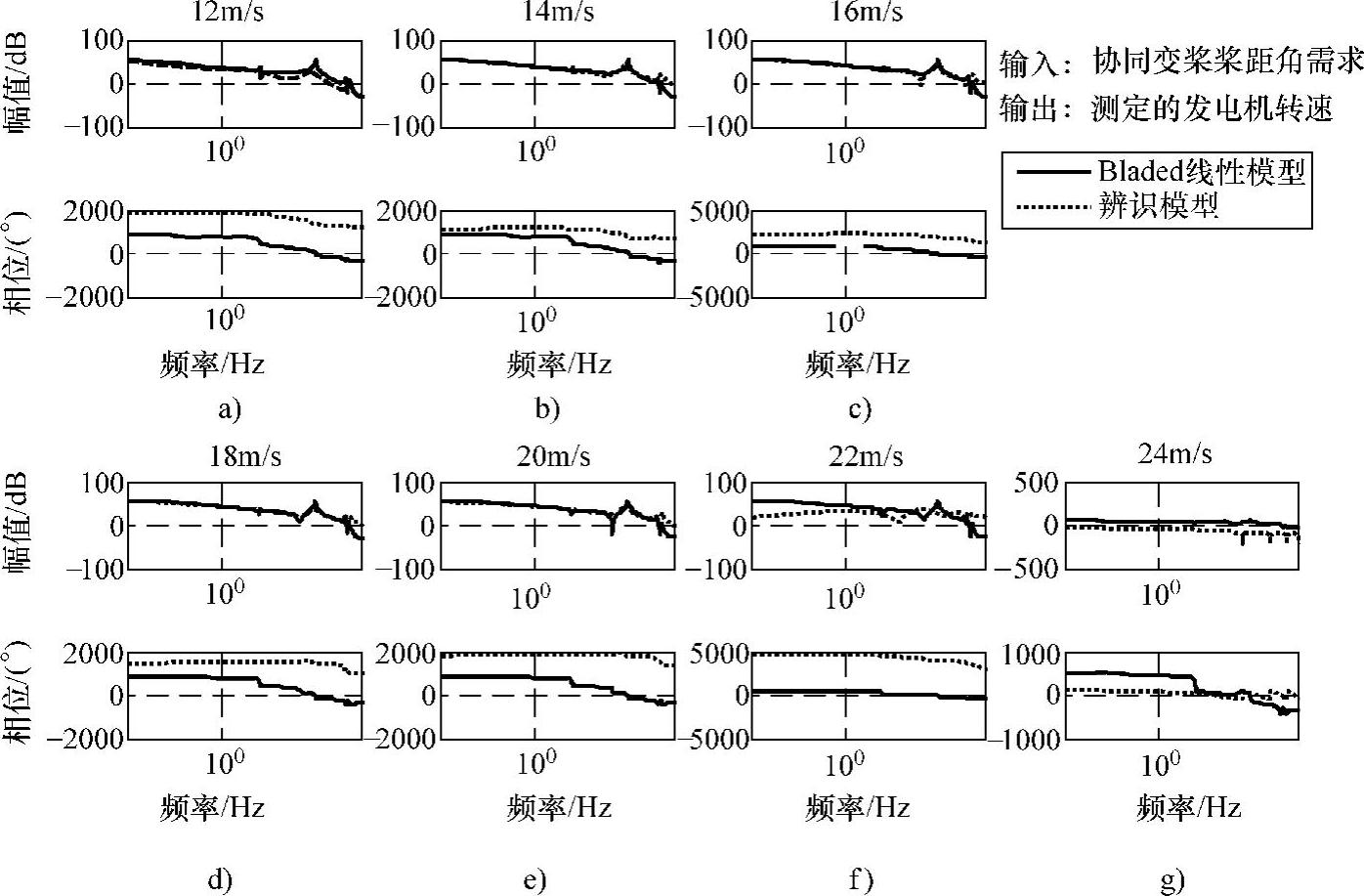
图10-48 当地线性模型辨识结果
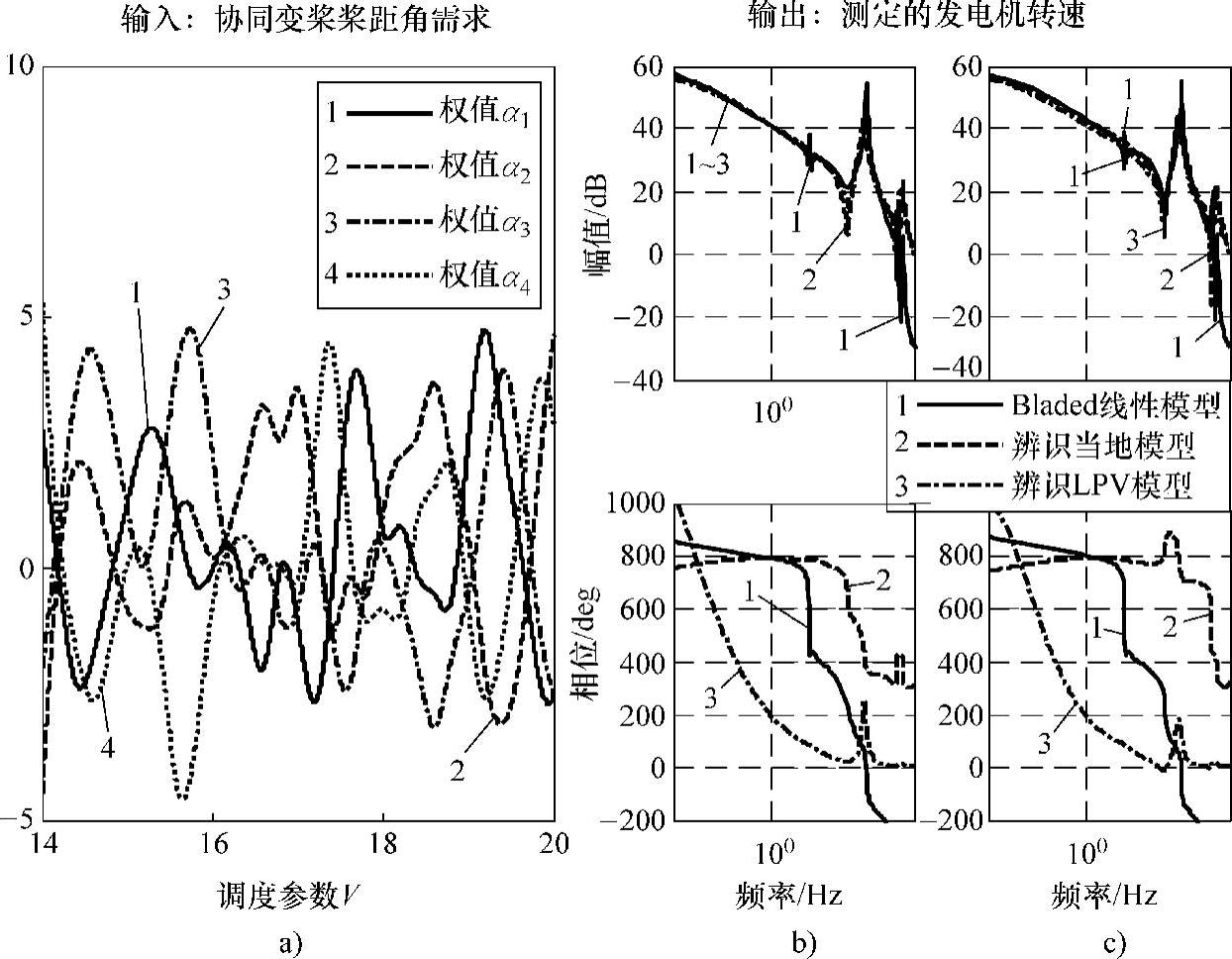
图10-49 LPV模型辨识结果
a）插值函数 b）伯德图（15m/s） c）伯德图（17m/s）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
