当地线性模型辨识：基于试验数据和ADALINE技术的优化方法

根据采集的试验数据，截取五个工作点数据分别辨识当地线性模型。这里我们可以采用直接法和两步法进行辨识，且均可以结合ADALINE框架。当采用直接法时，基于ADALINE方法即如图10-43所示；而当采用两步法时，其原理在于第一步估计从激励信号r₁到开环对象输入u的传递函数T₀（q^-1），然后利用该传递函数，第二步基于激励信号r₁产生无信号扰动的开环对象输入估计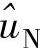，再辨识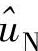到输出y的模型。则可利用的结构框架进行改良扩展，可得到图10-42所示的结构框图。

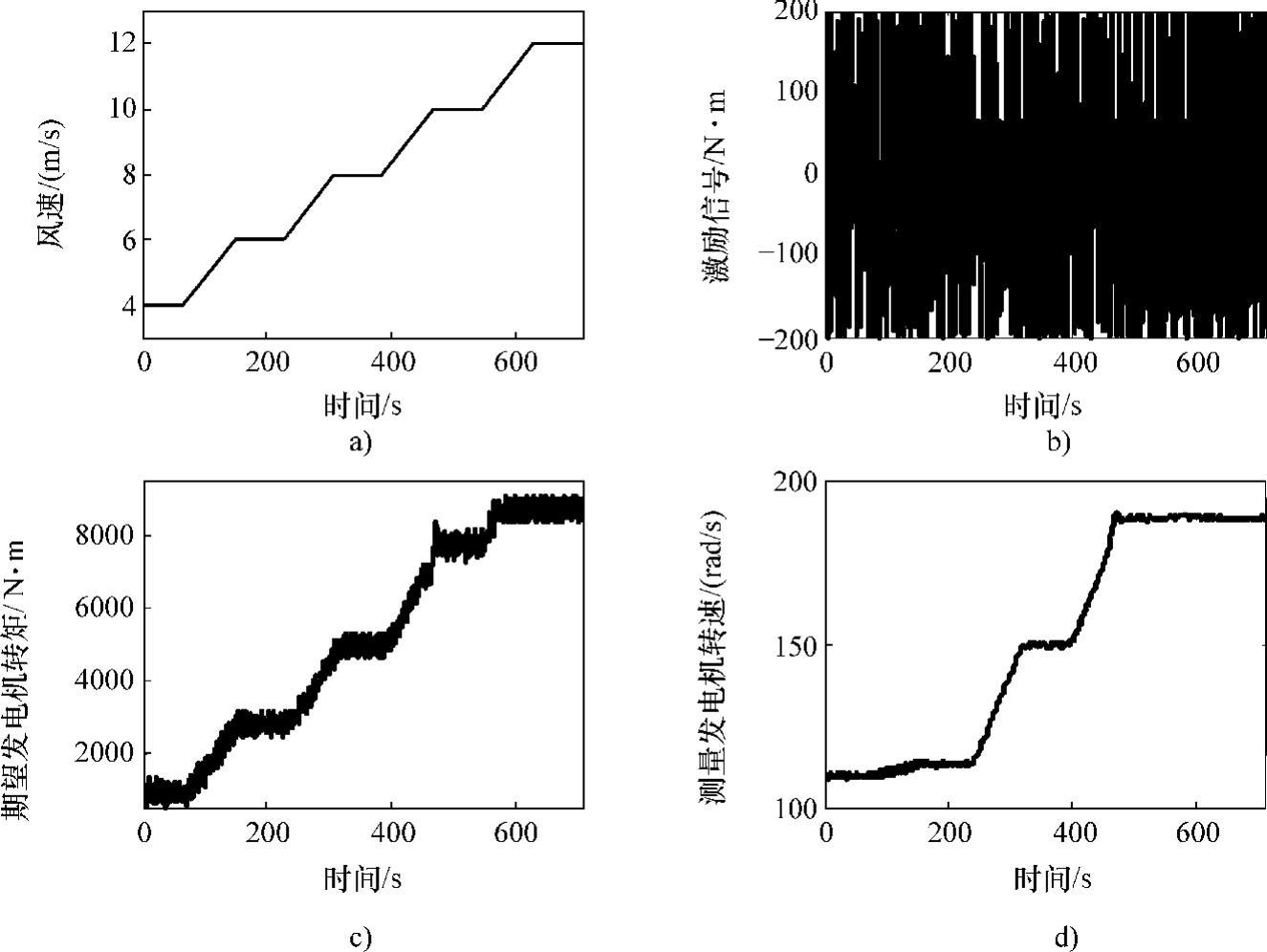
图10-41 全局测试试验数据

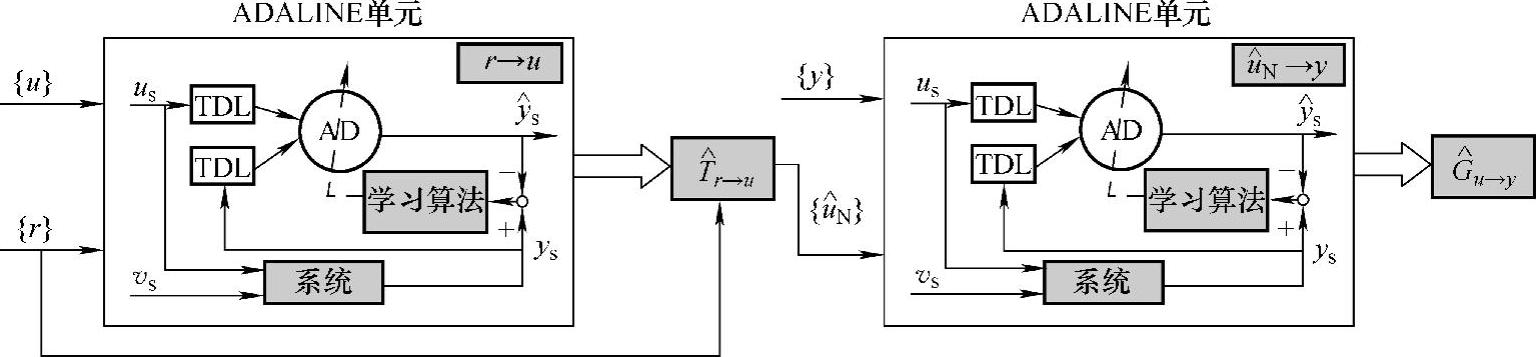
图10-42 基于ADALINE技术的两步法结构框图

以第二个工作点（6m/s）为例，采用基于ADALINE技术的方法进行辨识时，对应的结果如图10-43所示。可以看到，学习率也跟随训练过程调整直到适应系统，而从输出和误差来看显示出了较好的辨识效果。(www.xing528.com)

由于采用两步法进行当地工作点辨识需要两步估计和一步仿真输出，若利用ADALINE计算不仅加大了运算量，且收敛速度较慢，因此可以直接进行运算。最终获取的五个当地工作点伯德图比较如图10-44所示。可以看得除了在12m/s风速情况下，其他风速段的模型辨识结果基本吻合，这是因为12m/s附近为中低风速过渡阶段，转矩控制器与桨距控制器会进行耦合，产生一个复杂的联合控制区域，导致辨识和控制异常困难，因此结果性能较差；而其他工作点除4m/s外，低频段特性两步法均比直接法要好，且其他频段特性差别不大，因此可以采用两步法辨识所得的当地线性模型进行进一步插值。

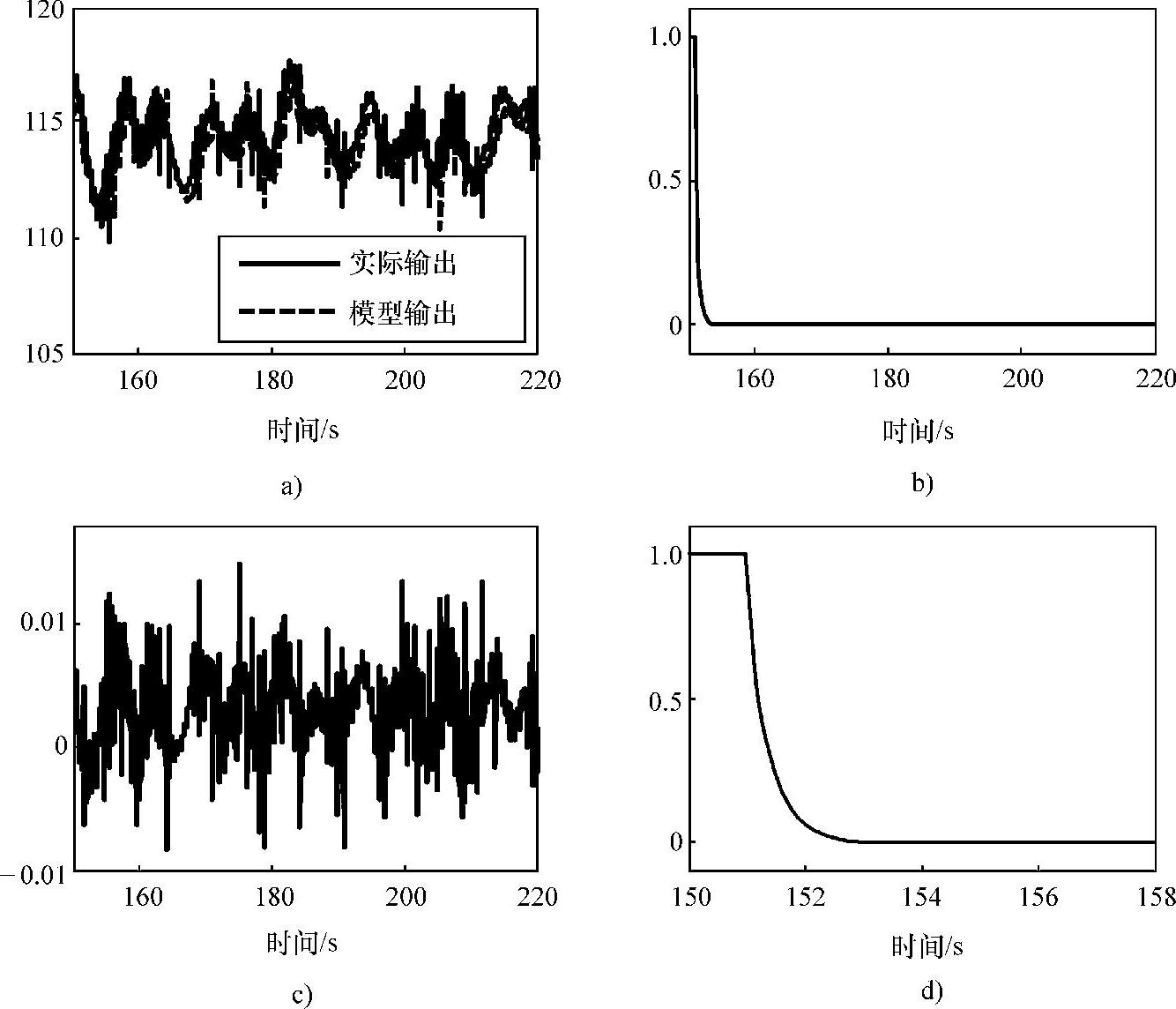
图10-43 基于ADALINE方法辨识结果（风速6m/s）

a）输出比较 b）学习率η变化轨线 c）模型相对误差 d）学习率η变化轨线（前200次）