基于Bladed线性模型的开环辨识优化方法

风电机组是大型昂贵的发电设备，其必须工作在闭环条件下，以避免机组运行失控而造成安全事故或经济损失，因此真实机组的系统辨识必须基于闭环条件测试。然而研究机组开环特性，以及分析基于开环情况下激励输入和系统输出的系统辨识，对于理解模型结构，以及后续的闭环辨识方法具有指导意义。

图10-20 模型离散化结果（风速8m/s）

1.辨识试验设计及数据获取

试验设计是获得可用于系统辨识的数据的前提，针对风电机组特殊情况，分析如下方案。

方案：基于Bladed线性模型的开环测试

由于Bladed提供了机理模型线性化工具，可以获取Bladed中不同风速工作点下的线性模型；同时，该模型在一定程度上可以视为Bladed中机理模型的良好近似。由此，可将导出的线性模型作为参考真实模型，对其进行开环激励测试实验。主要包含以下步骤（图10-21所示为软件操作步骤）：

图10-21 开环辨识试验设计软件操作步骤

模型线性化设置及生成linmod1.PJ结果；

计算线性模型linmod1.mat并导出；

导入MATLAB获取某个工作点传递函数模型SysModel（如8m/s）；

以SysModel模拟真实对象，在MATLAB中激励测试，获取输入输出数据[U，Y]；

根据输入输出数据[U，Y]辨识模型，并与SysModel进行比较。(www.xing528.com)

2.系统辨识结果

根据前述方案，以转矩环辨识为例进行说明。设置激励信号为伪随机信号PRBS，对象模型为Bladed导出的8m/s条件下转矩环即Generator torque demand到Measured generator speed线性模型。对应的输入输出信号如图10-22所示。

图10-22 开环辨识试验输入输出数据

此时系统未加测量噪声，同时结合Iribas提出的工程上适用的模型结构，选用ARX模型进行辨识。采用MATLAB系统辨识工具箱，计算不同模型阶次下的损失函数，图10-23所示为随着阶数增加损失函数变化曲线，可以看到在8～10阶的时候，模型就有较好的匹配结果。不妨即取模型结构为8阶，获取该情况下的ARX模型。图10-24所示为辨识ARX模型与Bladed线性模型的比较结果：图a为时域信息，可以看出辨识模型很好地在时域上对原模型进行了匹配；图b、c为波特图（剔除低频段），可以看出在几个关键频率点上，ARX模型基本能够辨识得到，只有中间左起第三个峰值无法获取，而实际上该峰值在降阶后的Bladed线性模型上也已经消去。

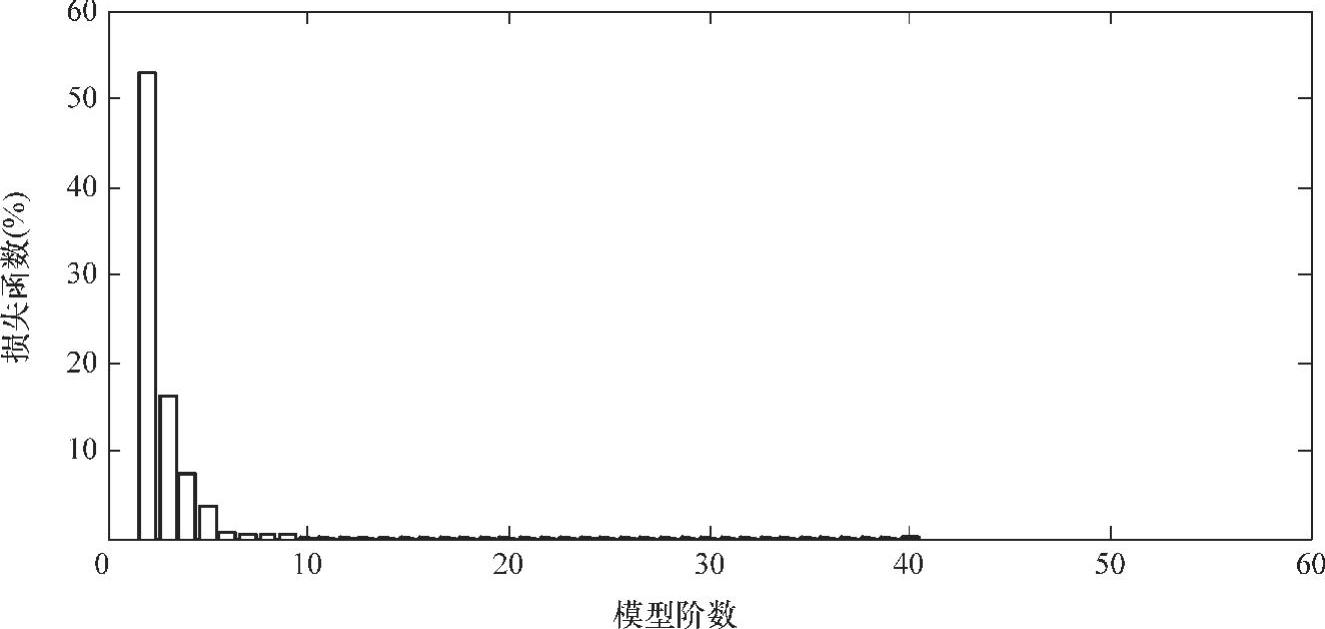
图10-23 损失函数随模型阶数变化曲线

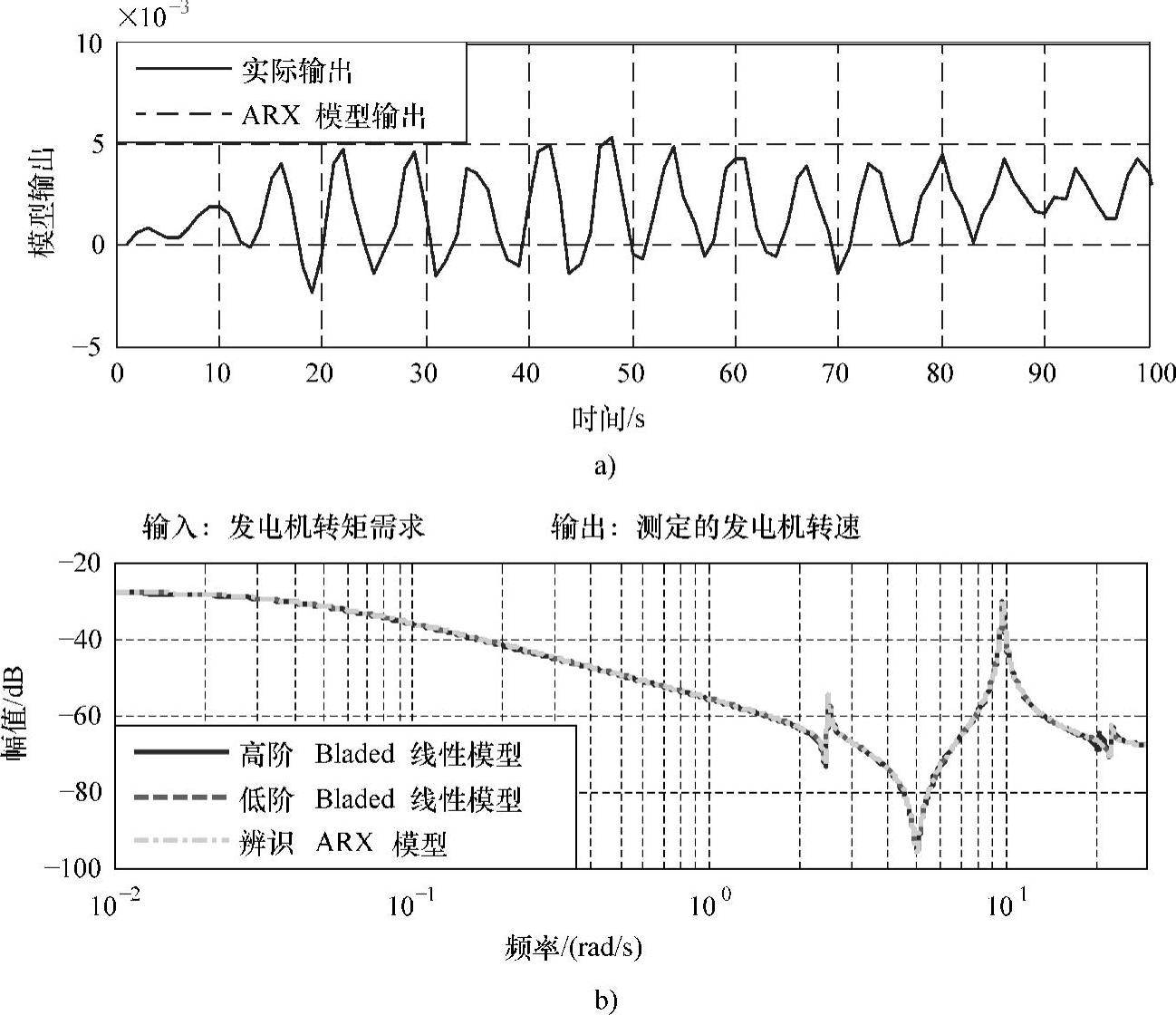
图10-24 开环辨识结果（风速8m/s）

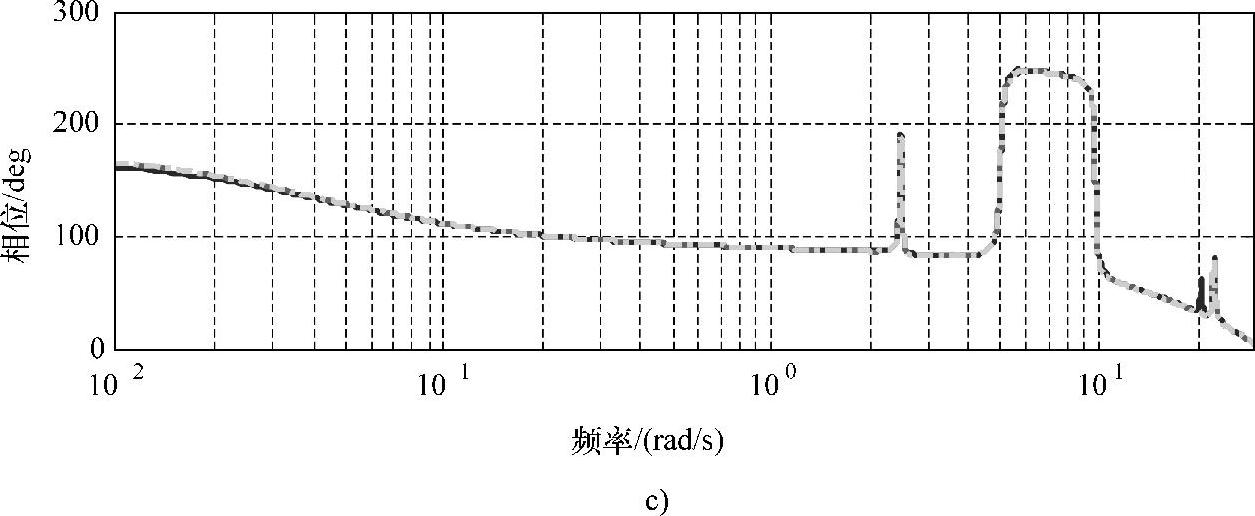
图10-24 开环辨识结果（风速8m/s）（续）

采用同样性质（频率和幅值）的激励信号，图10-25a、b、c所示为对应的桨距环开环辨识结果。可以发现，此时桨距环的相位估计比转矩环要差，尤其在第一个频率特征点尖峰处，辨识的结果具有反向相位的特性，这可能是此时低频段特性没有很好地被激励出来。于是改变信号频率，将频段范围包含较低频率信息，重新进行辨识试验，最终获得的辨识结果如图10-25d、e、f所示。此时，辨识结果较好地改进了低频段相位特性曲线。同时，从两边的幅频特性曲线来看，高阶系统在第一个频率特征处的波峰在低阶和ARX模型中均未能体现。