基于Bladed的风电机组线性化模型优化

1.线性化设置及模型的导出

Bladed提供线性化设置，然后根据设置计算线性化模型得到“linmod1.PJ”文件，即针对设置的风电机组模型计算各个整数风速点的稳态线性化模型；然后对线性化的计算结果进行后处理，可得到能够应用于MATLAB计算的“lin_- mod1.mat”文件。相关的操作设置如图10-12所示。

图10-12 线性化设置及线性化结果后处理

2.线性化模型传递函数获取

在MATLAB中加载“linmod1.mat”文件，可以查看其相关信息。

此时SYSTURB是一个状态空间方程模型，其A、B、C、D矩阵是下述方程的系数矩阵：

A、B、C、D数组在matlab里是3维数组，第一维是风速，包含范围4～25m/s共计22个分量。编写如下的MATLAB函数，可获取开环传递函数：

function sys=GetOpenLoopGs（SysTurb，WindSpeed，InputNum，OutputNum）

% SysTurb——linmod1.mat文件中的结构名称

% WindSpeed——风速点，范围为4～25m/s

% InputName——输入变量序号

% OutputName——输出变量序号

if WindSpeed＜4||WindSpeed＞25

此时在Matlab的command window输入如下：

这里取风速8m/s，输入为序号3即Generator torque demand（发电机转矩给定），2为Collective pitch angle demand（浆矩角给定），输出为序号1即Meas-ured generator speed（测速的发电机转速），即可得到：

转矩控制环伯德图如图10-13左图所示（图a为18m/s桨距控制环伯德图），此时所获取的线性模型是系统辨识结果的重要参考标准。

在获得系统开环传递函数之后，需要分析风电机组模型的关键信息，利用Bladed可以计算并绘制其坎贝尔图（见图10-14）。风力机相对振动频率单位（P）的定义为风力机单片桨叶旋转一周需要时间的倒数，单位（Hz）。假设某风

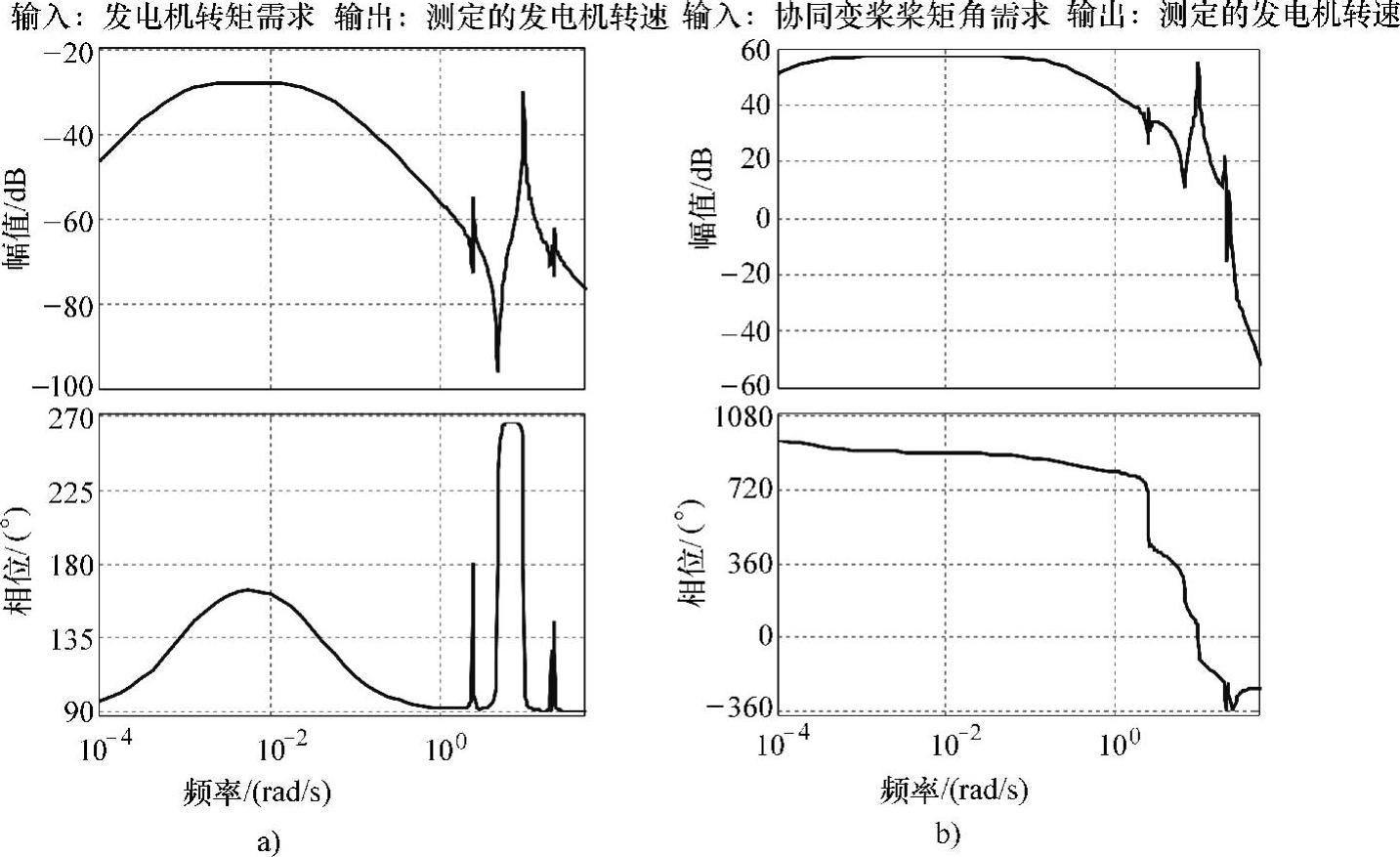
图10-13 开环系统伯德图

a）风速8m/s b）风速18m/s

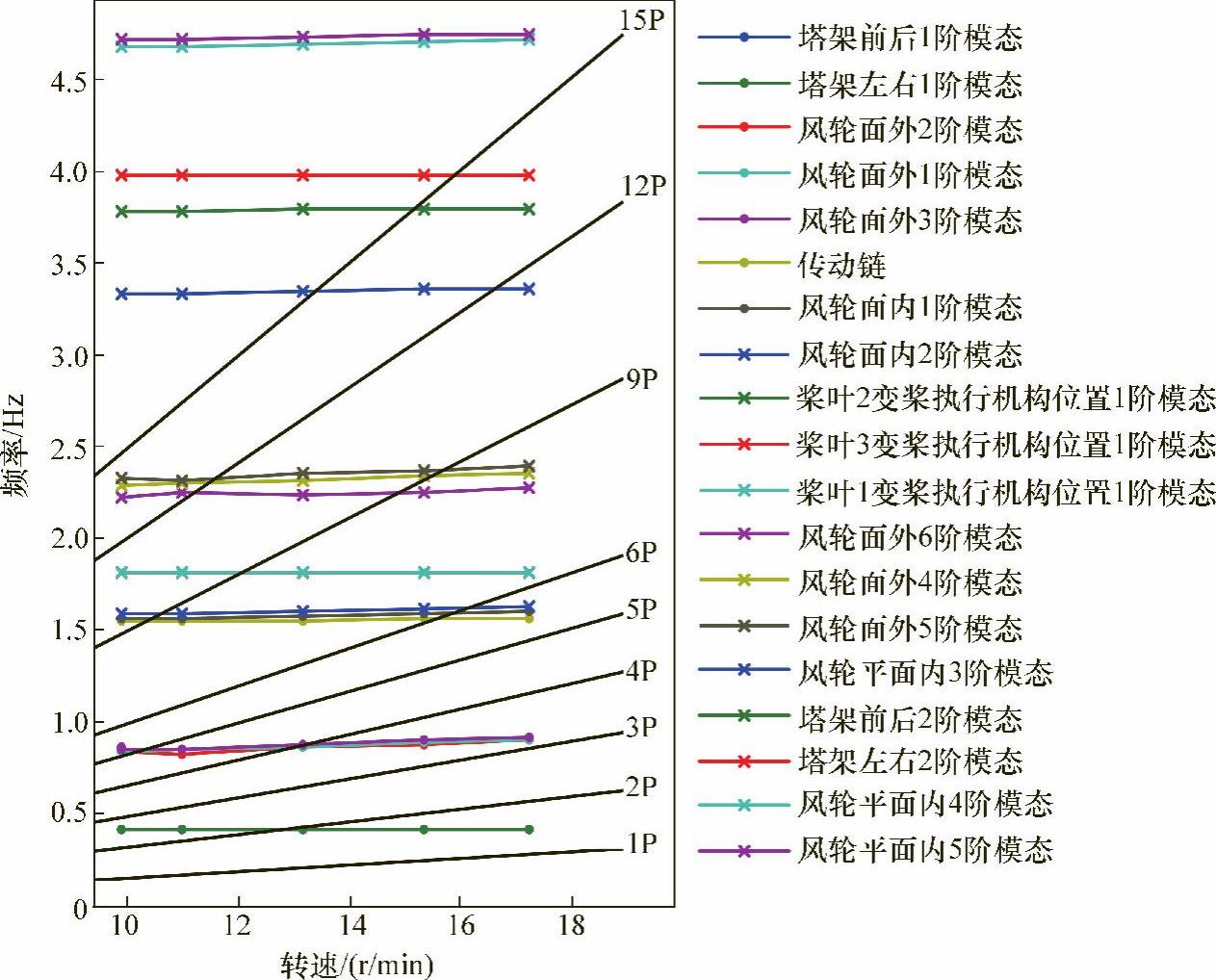
图10-14 风力发电机组Campbell图（彩图见封二）

电机组风轮转速为12r/min，则P=12r/min/60Hz=0.2Hz，此时可以看到塔架前后一阶频率（Tower fore-aft 1）为0.3991Hz，则其相对风轮旋转频率为0.3991/0.2≈2P。对于3桨叶风力发电机组，在设计的过程中要尽量避开3P、6P、9P、12P等3P的整数倍的振动频率。将开环系统波特图中各频率关键点，关联到坎贝尔图中，可以依次推出相应的关系。

由Bladed导出的线性模型初始阶数为高阶，此时对理解模型动态特性以及后续分析十分不利，因此可以对模型进行降阶。模型的降阶方法主要有Pade近似法、Routh近似法、连分式法、主导极点法、正交分解模型降阶方法、Krylov子空间模型降阶方法等^[30]。

（1）Pade逼近降阶法

Pade逼近是一种关于函数值的特殊类型的有理分式逼近法，它的思想是以尽量快的速度与泰勒级数展开式相匹配。设函数f（x）由下述幂级数所定义：

则当有理分式满足：(www.xing528.com)

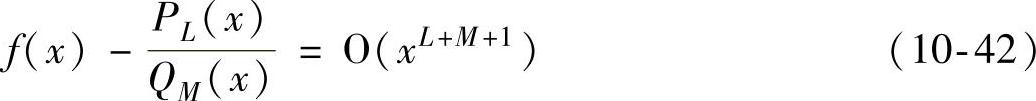
称有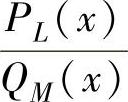为f（x）的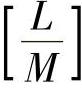阶Pade逼近。P_L（x）是一个次数最高为L的多项式，Q_M（x）是一个次数最高为M的多项式，且P_L（x）和Q_M（x）没有公因子。定义标准化条件为

Q_M（0）=1.0 （10-43）

将P_L（x）和Q_M（x）的系数表示如下：

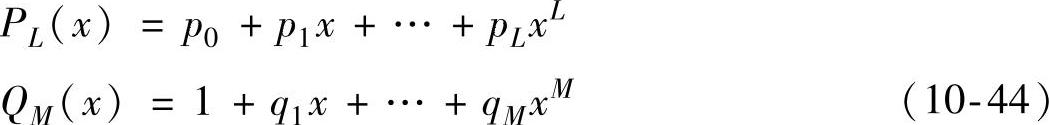
以Q_M（x）遍乘式（10-42）以线性化系数方程，比较系数可得

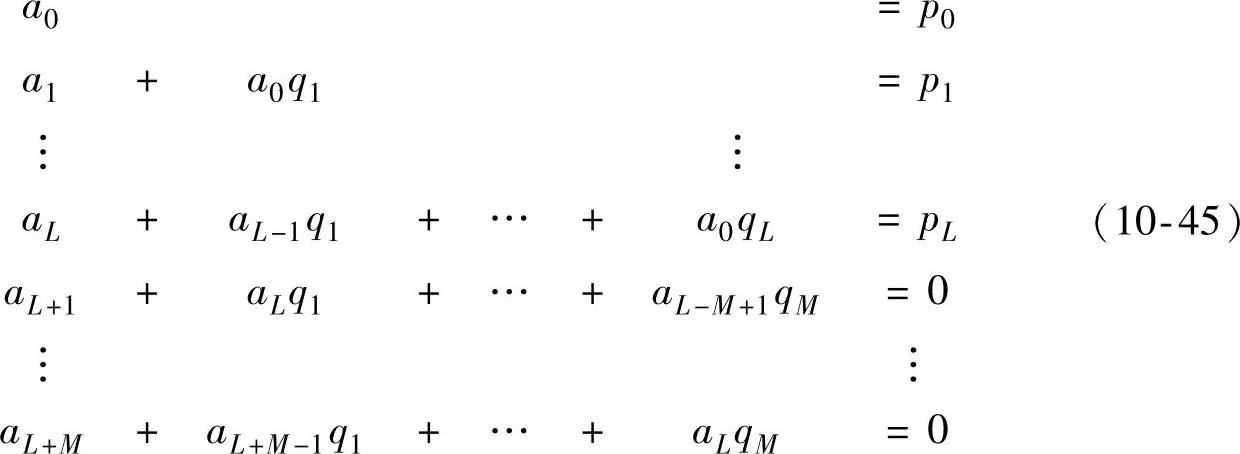
并满足a_n≡0（n＜0），q_j≡0（j＞M），求解该线性方程组即得各项系数p_i（0≤i≤L）以及q_j（0≤j≤M），代入式（10-44）即得Pade近似的分子分母多项式。

Pade降阶法因其计算的简易性和低频的良好近似性而被广泛采用，但存在一个很大的缺点即得到的简化模型不一定能保持原系统的稳定性。采用pade降阶法对原系统方程进行处理，其有一个优点是分子分母多项式的阶数可以不止差1，不妨取[9，10]和[8，10]阶模型，绘制阶跃响应和零极点图（见图10-15）。从图中可以发现，采用Pade法，降阶后系统会存在右半平面极点，导致系统不稳定，符合Pade法的特性。

图10-15 Pade降阶法不同阶数模型阶跃响应和零极点图

由前述伯德图和坎贝尔图分析，风力发电机组的模型需关注其频率特性，尤其在几个主要的频率特征点的信息需要体现出来。因此，绘制采用Pade降阶法获取的系统模型与Bladed中线性模型的伯德图比较结果（见图10-16），可以看到Pade法只逼近了低频特性，而高频段特性被抹去，无法表征出系统固有频率及模态，因此Pade不适用于此情景。

（2）Routh降阶法

Routh法是一种稳定的系统降阶方法，最初由Hutton[31]等提出，但最初该方法只能近似原系统的稳态响应或暂态响应，而不能两者兼备。为克服这一缺点，Shamash和Hsieh等对Routh方法进行了修正，使简化得到的模型既能同时近似原系统的稳态响应和暂态响应，又能保证系统的稳定性。Routh法因其计算的简易性、良好的近似性及能保持系统稳定性而获得了广泛的应用。

图10-16 Pade降阶法不同阶数模型与Bladed线性模型伯德图比较（风速8m/s）

若渐近线稳定的高阶系统模型的传递函数为

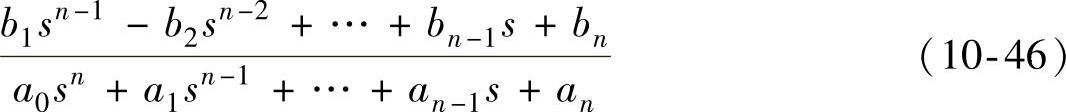
则其总能展开成下述典型形式：

式中：且f_j（s），（j=2，3，…，n）由下式确定：

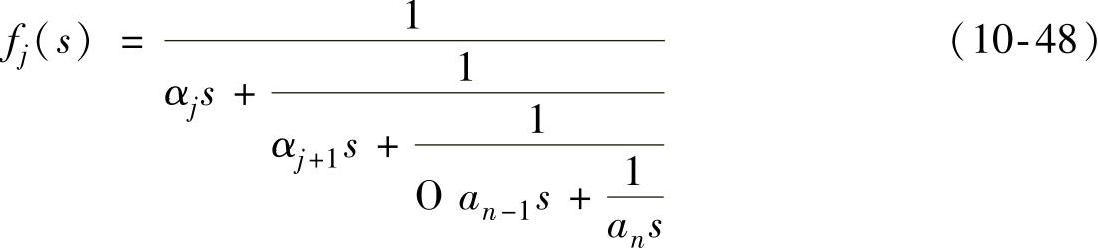
式中的系数α-β均由经典的Routh阵列求得。

采用Routh降阶法对原系统进行降阶，采取10阶、20阶、30阶模型，结果的阶跃响应以及零极点图如图10-17所示。此时，不论降阶后系统阶次，在阶跃作用下，系统的暂态和稳态响应得到了完美的复制，且稳定性没有发生变化。而从零极点图来看，右半平面不存在极点；但10阶和20阶的时候右半平面有零点，与原系统会有冲突；而30阶的时候比低阶更接近原系统的零极点特性，但仍然存在一定差异。

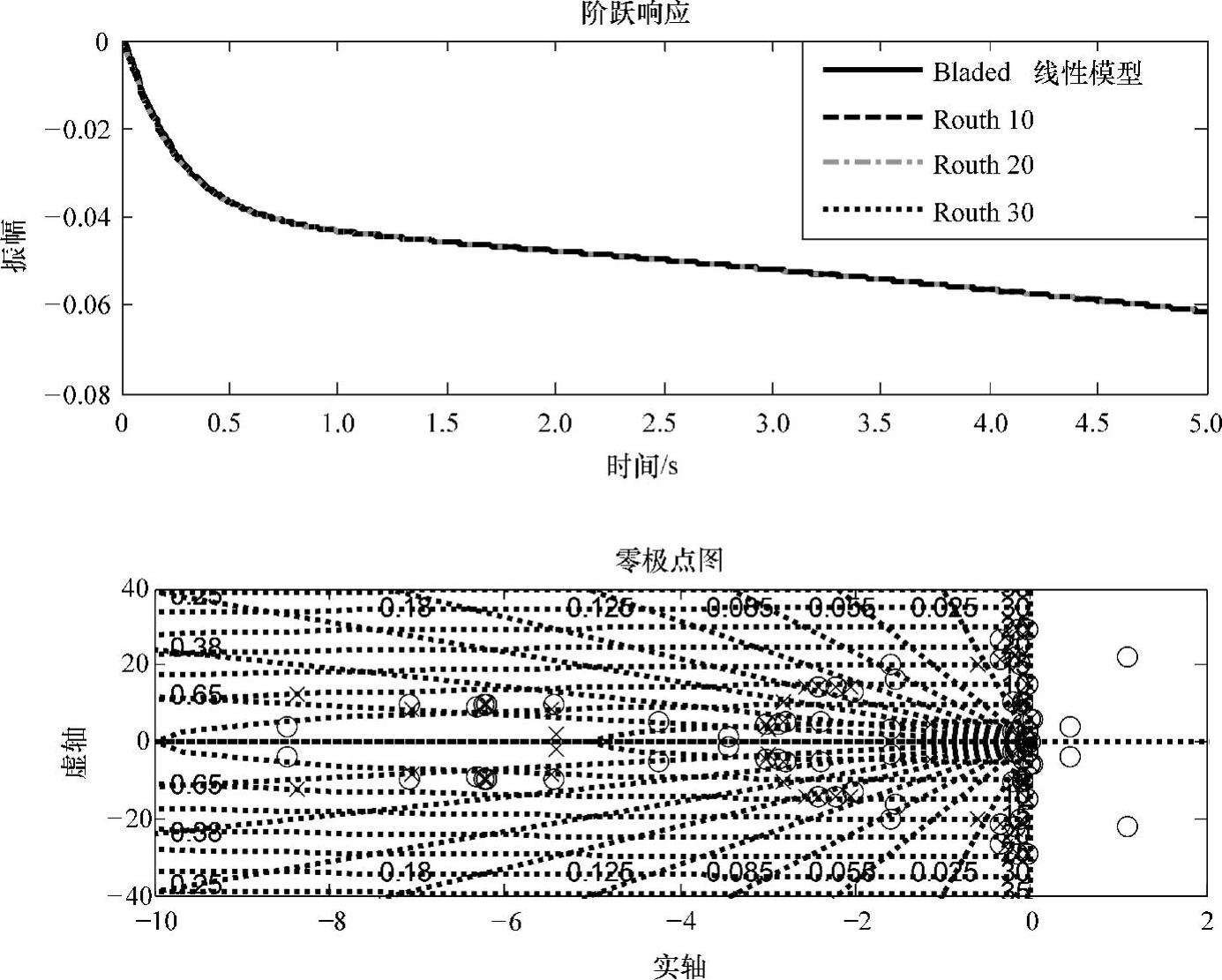
图10-17 Routh降阶法不同阶数模型阶跃响应和零极点图

同样，绘制降阶后模型与Bladed线性模型的伯德图比较如图10-18所示，可以看得即使阶数较低（如10阶），模型的低频段特性符合度仍然非常好，但是高频段拟合效果较差；而当模型阶数增加时，不会改变低频段特性的逼近效果，相反高频段特性会逐步得到改善。对其高频部分幅频特性曲线进行放大后，可以看到在频率2.68Hz处，10阶即开始出现差异；模型20阶在8.91Hz处出现差异；而30阶模型只在[15.1，26.9]Hz范围内具有一定差异，但此时模型阶数已经较高，并没有很好地降低模型复杂性，而且此时22Hz附近频段的两个波峰位置发生了较大的偏移。

（3）最小实现

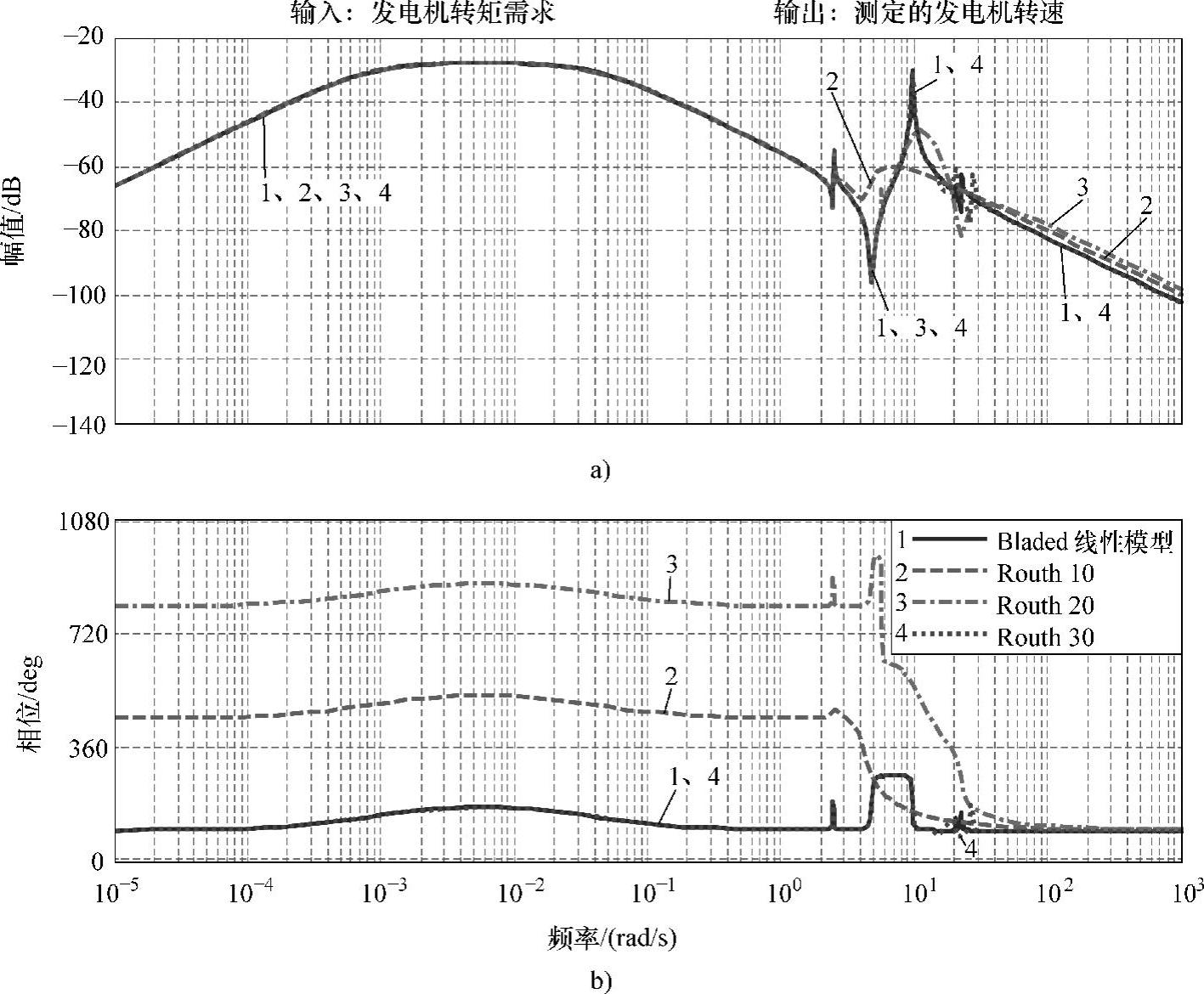
图10-18 Routh降阶法不同阶数模型与Bladed线性模型伯德图比较（风速8m/s）

根据对系统零极点特性分析，可以看到实际上系统有多对零极点位置几乎一样，如果能够解耦掉这些相近的零极点对，则可以较好地降低模型阶数。对于已规定的输入输出关系，或者某一给定的传递函数阵，状态变量的选择并不是唯一的，因此将有无穷多的状态空间表达式与之对应，即一个传递函数阵描述着无穷多个内部不同结构的系统^[32]。为实现命题的解，在阶次上可以不同；同样是最低的实现，由于状态变量可以选择，其解也可以多式多样。从工程的观点看，在无穷多个内部不同结构的系统中，其中维数最小的一类系统就是最小实现问题^[33]。对于Bladed线性模型，消去解耦零极点对，获取最小实现。图10-19所示为该方法降阶后的结果（这里取的容忍度为0.01），图a、b所示为阶跃响应和零极点图，可以看出，对于稳态增益会有一定影响；对应到伯德图（见图c、d）比较，恰好反映出中低频段特性差异；而在高频段特性，可以看出此时获得的模型具有极好的一致性。

MATLAB提供了可供选择的连续系统离散化方式，只需调用c2d命令即可进行离散化，其包含零阶保持器（zoh）、Tustin、线性插值（foh）、匹配零极点（Matched）等方法，在图10-20中给出了几种离散化方式所得模型的伯德图比较。从比较结果可以看出，采用Tustin方法进行离散化时，其在10Hz时的频率特性发生了改变，且后续的特性具有一定的偏差，更重要的是高频段的两个波峰特性发生了严重的移位；foh方法的相频特性与原始模型吻合度最好，但其幅频特性具有一定的误差，尽管其误差比Tustin方法要小；而zoh方法和matched方法幅频特性估计基本一致，且要优于其余两者离散方式，但相频特性却在10Hz处有一个倾斜的偏移量。因此根据实际情况，可以选择合适的离散方式，我们主要关心其幅频特性，因此选择zoh方法获得的模型作为离散化模型，且将此模型作为后续辨识所得结果的验证模型。

图10-19 最小实现模型与Bladed线性模型伯德图比较（风速8m/s）