从ADALINE到LPV：一种新的系统辨识方法

基于LPV的系统辨识方法可分为两步：第一步是当地线性模型的获取；第二步是基于插值函数的全局LPV模型获取。在获取工作点p_k（k=1，2，…，m）的当地线性模型时，需依次对各对应工作点采集的数据进行辨识处理，m个工作点就需要进行m次计算，倘若所要辨识的当地模型个数较多，重复性工作量将会较大；而在全局LPV模型获取阶段，最终的θ估计问题在直接进行式（10-29）计算的时候，若数据量较为庞大、三次样条的阶数较高，则会产生病态或者难以求解的问题。可采用一种基于ADALINE技术的系统辨识方法。

1.基于ADALINE技术对稳定工作点进行辨识

在稳定工作点p_k（k=1，2，…，m）上，将系统模型表达式（10-23）展开即为

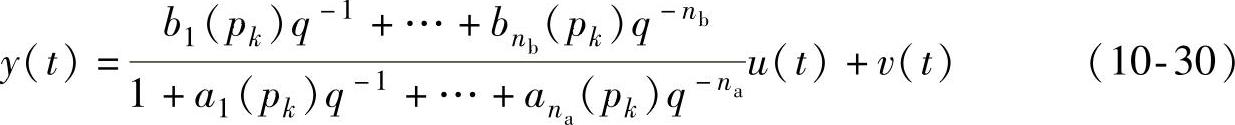
此时，要估计的模型参数即为a_i，b_j（1≤i≤n_a，1≤j≤n_b，n_a≤n_b），采用图10-7所示的框架。

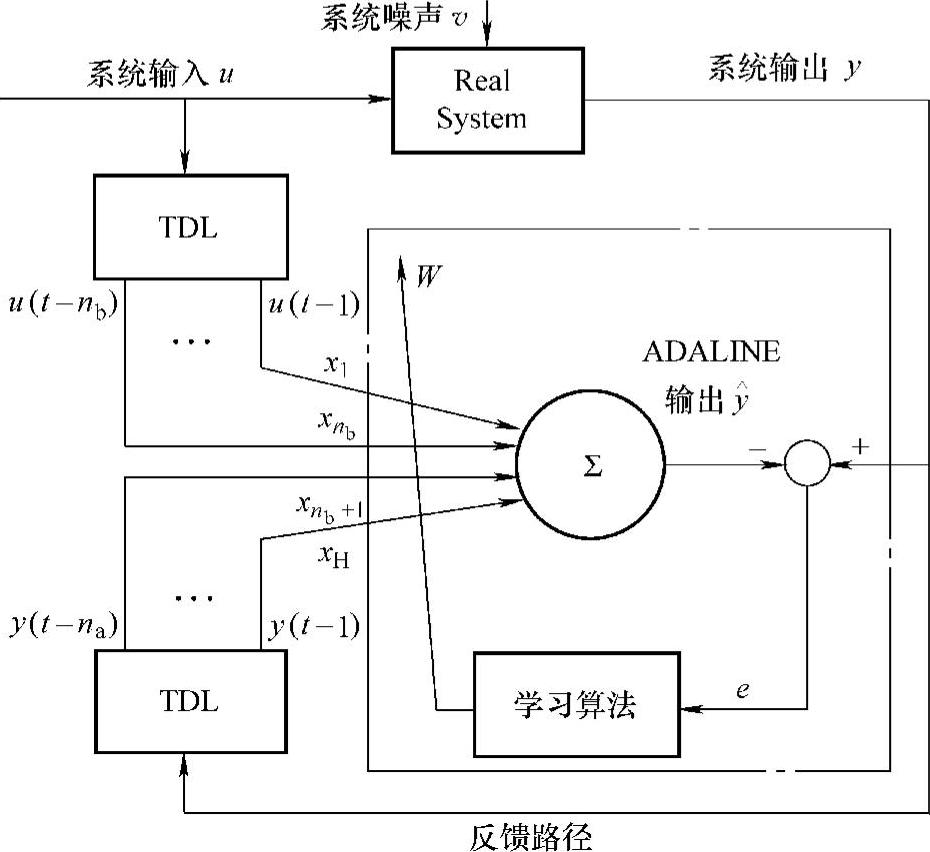
图10-7 基于ADALINE技术辨识稳定工作点的方法结构示意图

此时，点画线框为一个ADALINE模块，其输出为输入的线性组合。当输入端加入串联TDL（单位延迟控制器）的系统输入、输出信号后，则有新的ADA-LINE输入为

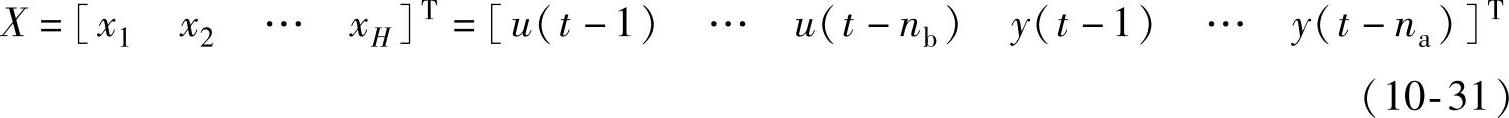
这里t为迭代指数，u（t）、y（t）分别为系统输入、系统输出，相应权值为

则有ADALINE输出：

通过学习算法，使得权值的估计值[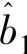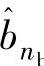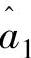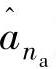，…，，，…，]在经过训练后不断地趋于真实的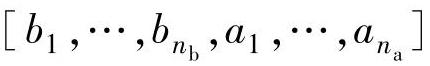，则ADALINE可视为真实系统的良好近似，由此确定各稳态工作点模型为

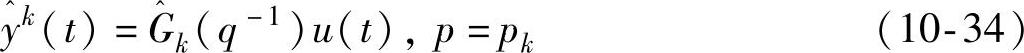
2.基于ADALINE技术对全局LPV模型进行辨识

以三次样条函数为例，针对式（10-25）～式（10.29）情形，设计合理的辨识结构框架。将全局系统输入u（t）通过式（10-34）中传递函数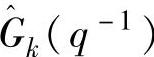获得的估计值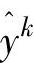，与对应的式（10-26）中的调度参数矢量运算所得的结果作为ADALINE输入，如图10-8所示。此时有对应设计：

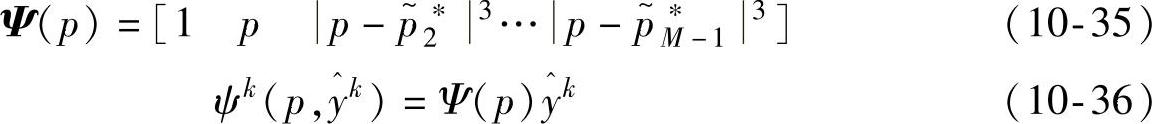
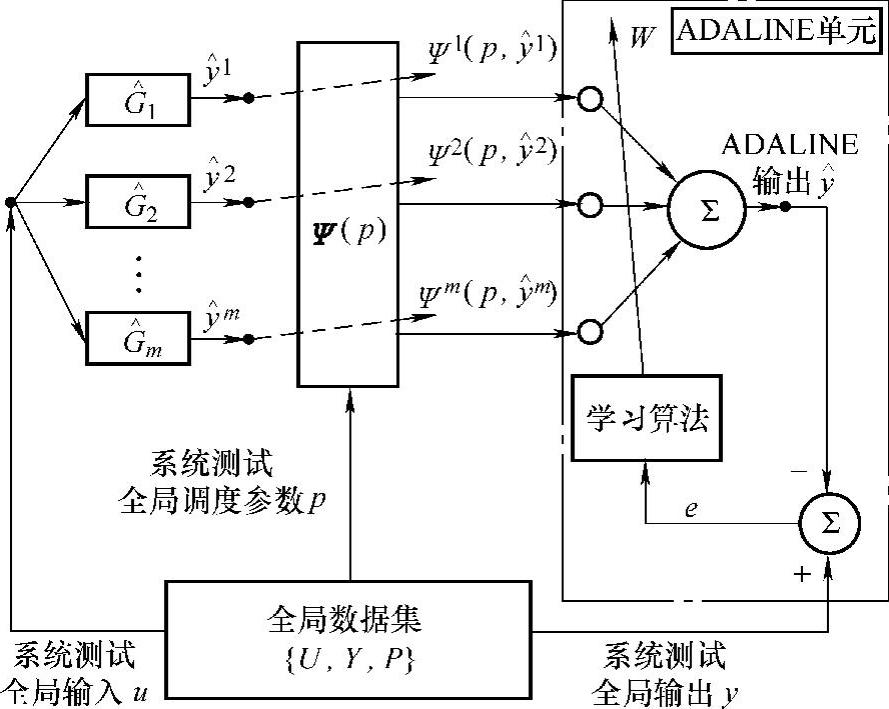
图10-8 基于ADALINE技术辨识全局LPV模型的方法结构示意图

则全局LPV模型的输出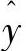的表达式为

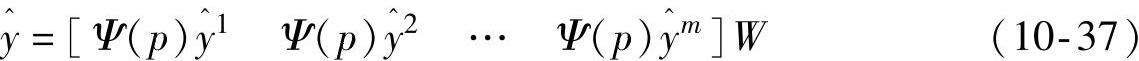
将式（10-37）与式（10-28）相比较，能够得出W的估计即为θ的估计，如此即建立好全局系统的LPV模型。模型的精确性能够通过迭代停止准则和基于ADALINE的网络规模改进来调节，以达到要求的模型精度。

3.学习算法(www.xing528.com)

为更好地提高算法的速度与收敛性，可采用了滑移窗以及学习率更新的机制，对应的学习算法如下：

给定如下SISO系统模型：

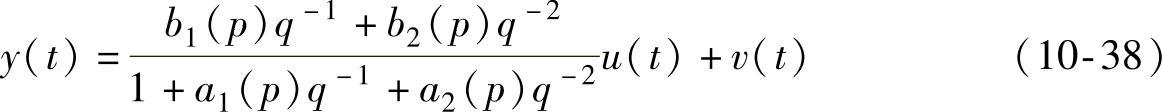
式中：p∈[1.0，5.0]；v（t）为滤波噪声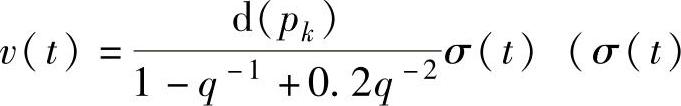为白噪声序列且d（p_k）使得噪声信号为无噪声信号功率的3%），分子、分母多项式参数满足：

系统测试为全局激励测试，采用GBN信号以及如下测试方案：

1）工作点p₁=1.0处，持续激励1000s；

2）调度参数变量p₁从1.0均匀变化到2.5，持续激励1000s；

3）工作点p₂=2.5处，持续激励1000s；

4）调度参数变量p从2.5均匀变化到5.0，持续激励1000s；

5）工作点p₃=5.0处，持续激励1000s。

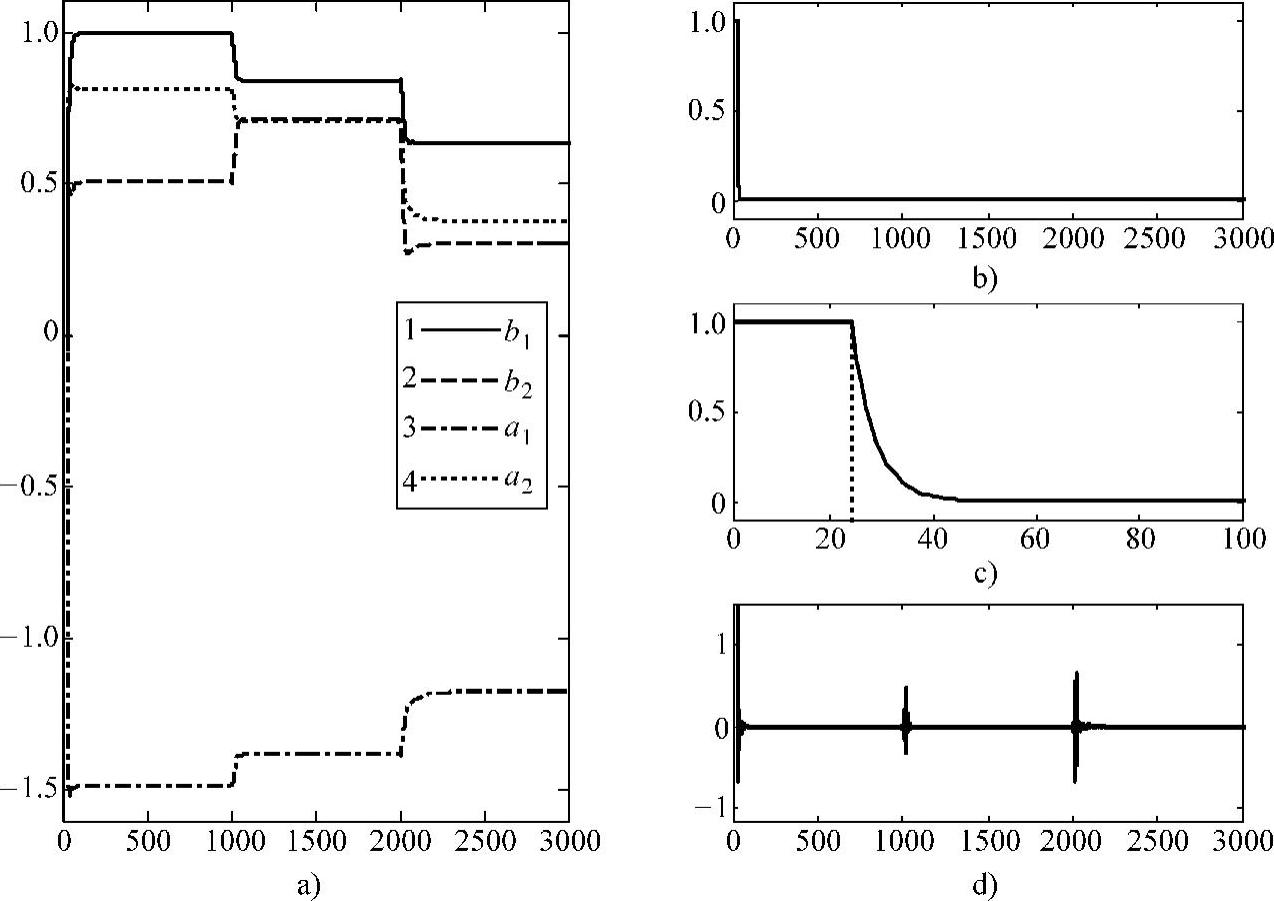
图10-9 基于ADALINE技术辨识全局LPV模型的方法结构示意图

a）模型参数估计 b）η变化曲线 c）η变化曲线（前100步） d）模型误差

获取测试输入输出数据后，可以截取三个工作点数据辨识出三个当地线性模型，相应的辨识结果如图10-9所示。由图a可以看到，对于从某一稳定工作点切换到另一稳定工作点的系统，该方法能够很好地在较短学习时间之后跟踪系统参数。同时依据ADALINE的自适应性，可以将原本针对三个工作点依次进行辨识的次数降低为一次。从图b、c可以看出，学习率在训练伊始，会根据学习算法自动调整，而当调整到适应系统特性之后，则维持恒定的值。图d模型误差曲线，可以看到只有在切换工作点的时候，会有短暂的较大偏差，而其他区域误差均接近于零。

根据所得的三个当地线性模型，通过插值函数即可得到全局LPV模型，相应的结果如图10-10所示。此时设置的系统迭代停止准则为达到某一误差精度即停止，可以看到估计的权值函数并没有非常光滑，但其对应的不同调度参数p下的阶跃响应对比结果已经很好，但在p=3.9，4.5处均可以看到有一定的稳态偏差。

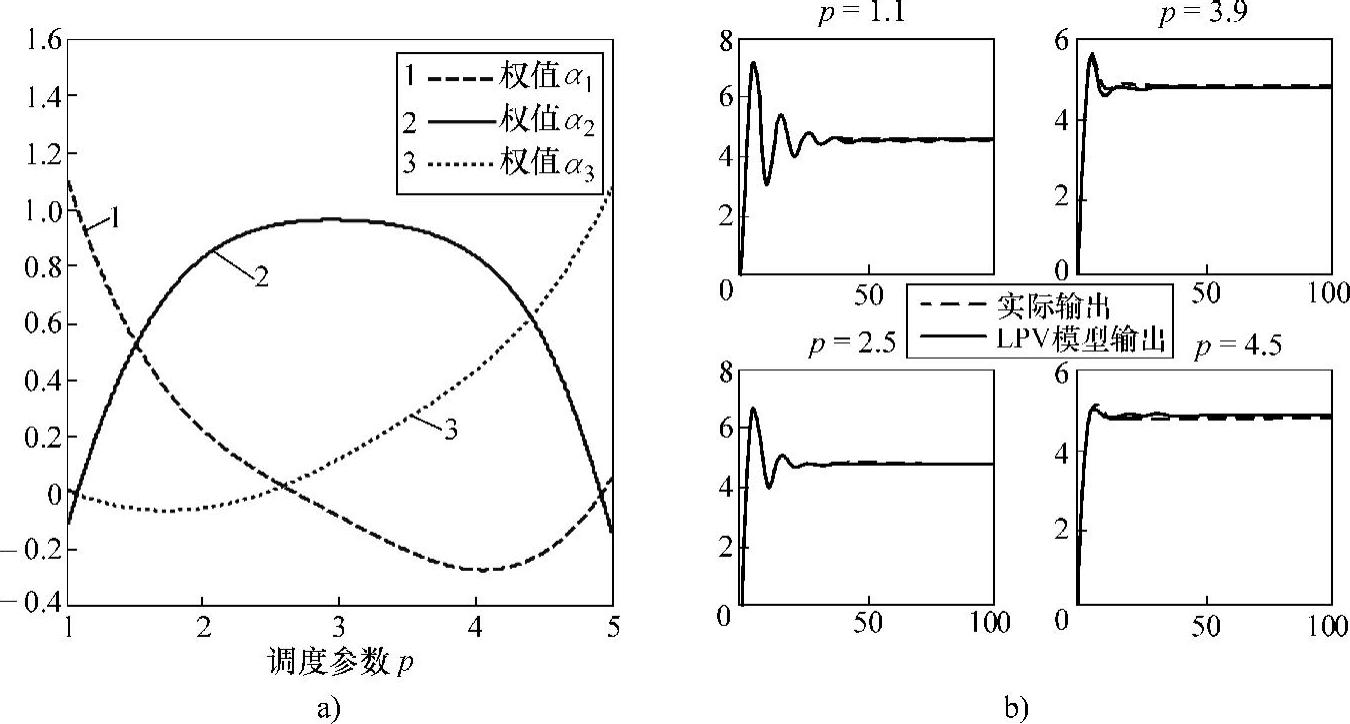
图10-10 辨识结果

a）插值系数随增量调度系数变化 b）系统单位阶跃响应对比

设置更高精度的迭代停止准则，再一次进行全局LPV模型辨识后，则能获取如图10-11的结果。此时，估计的权值函数在对应的三个工作点处，恰好满足理想权值（如p₁=1.0处满足α₁=1，α₂=0，α₃=0）。而从相应的阶跃响应对比可以看得，p=3.9，4.5处的稳态偏差已经消除，因此要优于前述权值估计。当然，此时要耗费比前述更多的计算内存和计算时间，当精度要求并不是非常高的情形下，可采用前述结果。

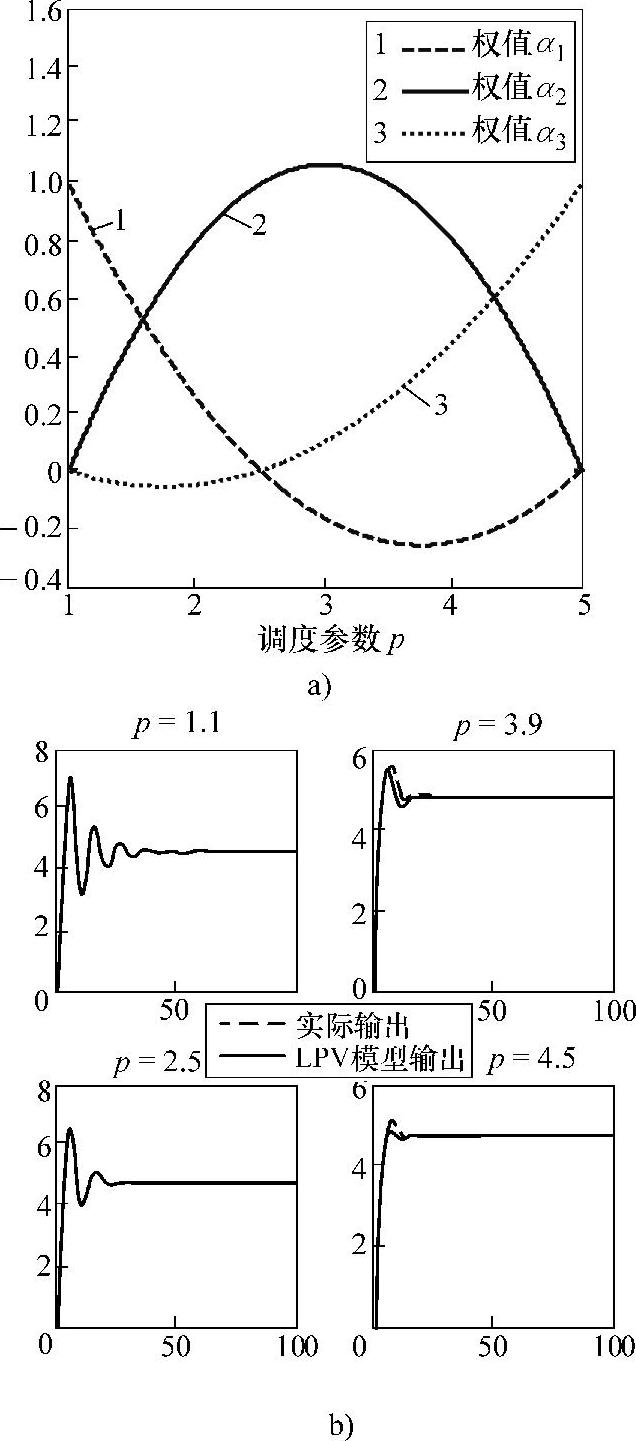
图10-11 更高精度准则下的辨识结果