系统模型与辨识方法的优化

1.传递函数模型

传递函数的辨识是经典控制理论中不可缺少的环节，其主要包含时域法和频域法两种。时域方法包括脉冲相应法、阶跃响应法和矩形脉冲相应法等，其中阶跃响应法为最常用方法。用阶跃响应方法辨识的对象主要有一阶惯性滞后环节、二阶等容惯性对象、二阶等容惯性加零点对象、二阶惯性加零点对象、高阶自衡对象等，相关的辨识方法多采用两（多）点法^[28]。频域法一般可由试验测得系统频率响应，然后根据频率特性拟合的Levy法获得系统传递函数。

2.模型形式与辨识方法

线性时不变系统是系统辨识中常用的模型，模型特性可通过脉冲相应、频率响应、功率谱或者谱密度等非参数模型描述，也可以采用输入输出差分方程、状态空间方程、传输函数等参数模型描述。对于非参数模型辨识方法，常用的有相关分析法、谱分析法等，且可以通过脉冲响应或频率响应转化为参数模型。而最小二乘法、极大似然法、预报误差法以及卡尔曼滤波法等常作为参数辨识方法。对于非线性系统，可通过小扰动理论建立参数线性变化的非线性模型，或采用神经网络模型、模糊模型等非线性模型建模。

3.最小二乘法原理

最小二乘法是一种经典的数据处理方法，由18世纪末高斯（K.F.Gauss）在行星轨迹的计算中提出。最小二乘法是系统辨识中是基本的参数估计方法，既可以用于动态系统，也可以用于静态系统；既可以用于线性系统，也可以用于非线性系统；既可以用于离线估计，也可以用于在线估计。

给定单输入单输出（single-input single-output，SISO）系统数学模型为

A（q^-1）y（k）=B（q^-1）u（k）+e（k） （10-5）

式中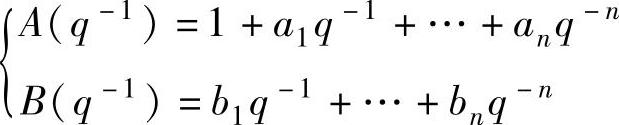，，q^-1为后移算子，则模型可以改写为

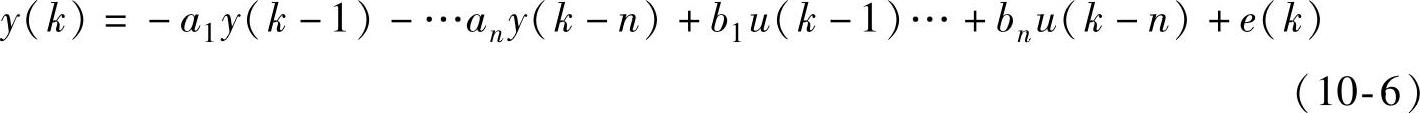
此时若已知输入和输出序列{u（k），y（k）}，为求参数a_i，b_i，i=0～n的估计值，引入向量：

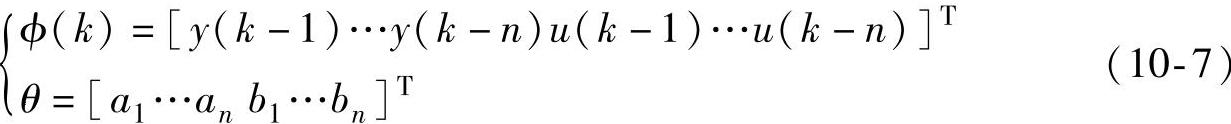
则式（10-5）可以改写为

y（k）=φ^T（k）θ+e（k） （10-8）

假设θ的估计值为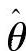，则

引入最小误差准则：

则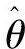为使得式（10-9）取最小时的θ值，而：(www.xing528.com)

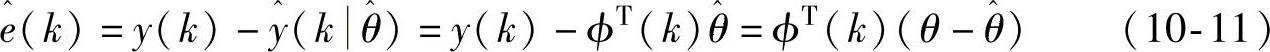
则式（10-10）的指标即为残差的二次方和，取k=n+1，…，n+N，共计N次观测，记：

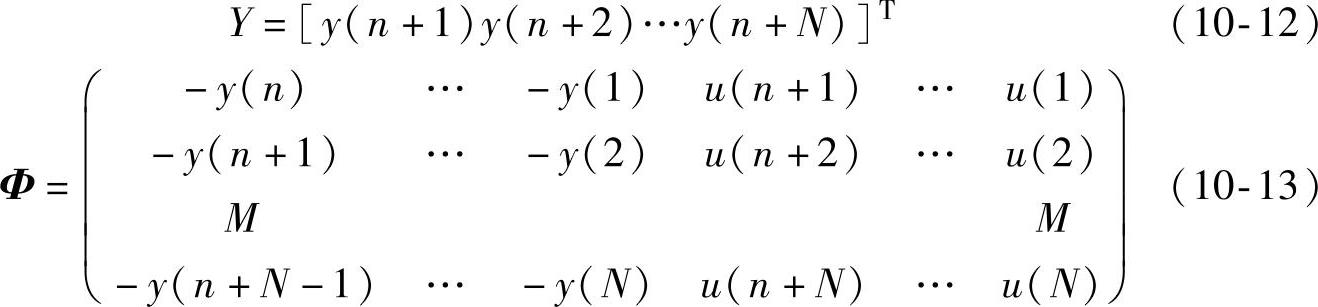
可得矢量形式的线性方程组：

Y=Φθ+e （10-14）

则按照下述准则函数来求取：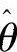

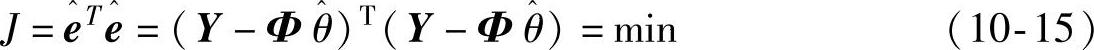
根据J对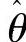求偏导，并令偏导数为0，可得

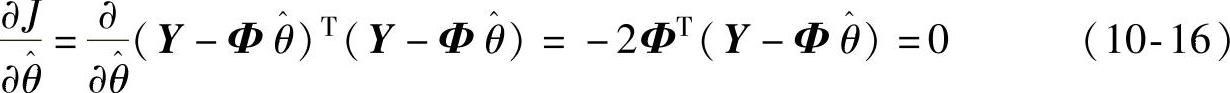
即有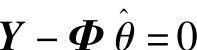得

当Φ^TΦ非奇异时，有

此时的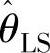称为最小二乘估计值，对应的方法叫作最小二乘法，以最小二乘法为基础的有递推最小二乘法、增广最小二乘法、广义最小二乘法、辅助变量最小二乘法等估计方法，用以解决不同的系统参数结构下的辨识。将一般的模型结构集写成下述形式：

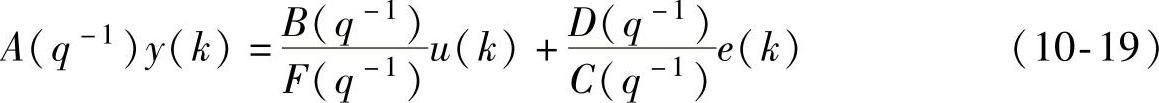
则对应的参数（多项式）与模型结构详见表10-1。

表10-1 式（10-19）中参数与模型结构关系