数据预处理与输入设计策略

系统辨识的准确度不仅与模型辨识和参数估计方法有关，还与试验数据所含待估计参数的信息量以及试验数据的测量准确度有关。合理选择辨识的输入信号是获得良好辨识结果的前提之一。常用的输入信号如下：

1.叠加正弦波

考虑系统响应频率范围内多个正弦波叠加为输入信号：

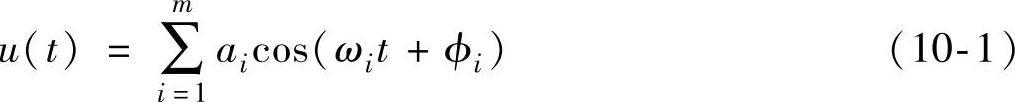
对其进行傅里叶变换得到频谱函数为

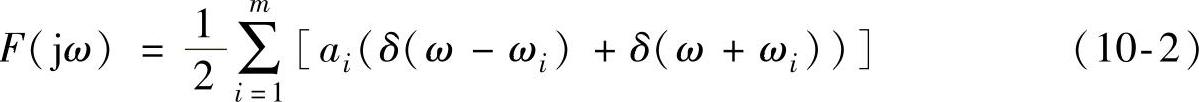
2.白噪声

白噪声是一种均值为零，谱密度为正常数的平稳随机信号，即满足：

E{u（t）}=0，R_u（t）=σ²δ（t） （10-3）

式中，δ（t）为狄拉克分布函数，即

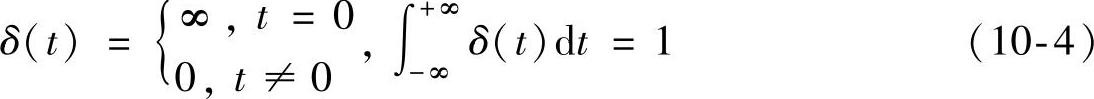
白噪声序列的产生方法有很多种，如乘同余法、混合同余法等。通过（0，1）均匀分布的白噪声序列的近似抽样统计，可以获得高斯白噪声信号；而白噪声序列经过线性环节滤波之后，可以得到滤波白噪声（有色噪声）信号；Tulle-ken提出一种广义二进制噪声信号（GBN），其基于转换概率使得GBN信号在两个值-a和a之间转换，产生适合于工业过程的控制相关辨识的实验信号^[27]。图10-2展示了几种不同白噪声信号。(www.xing528.com)

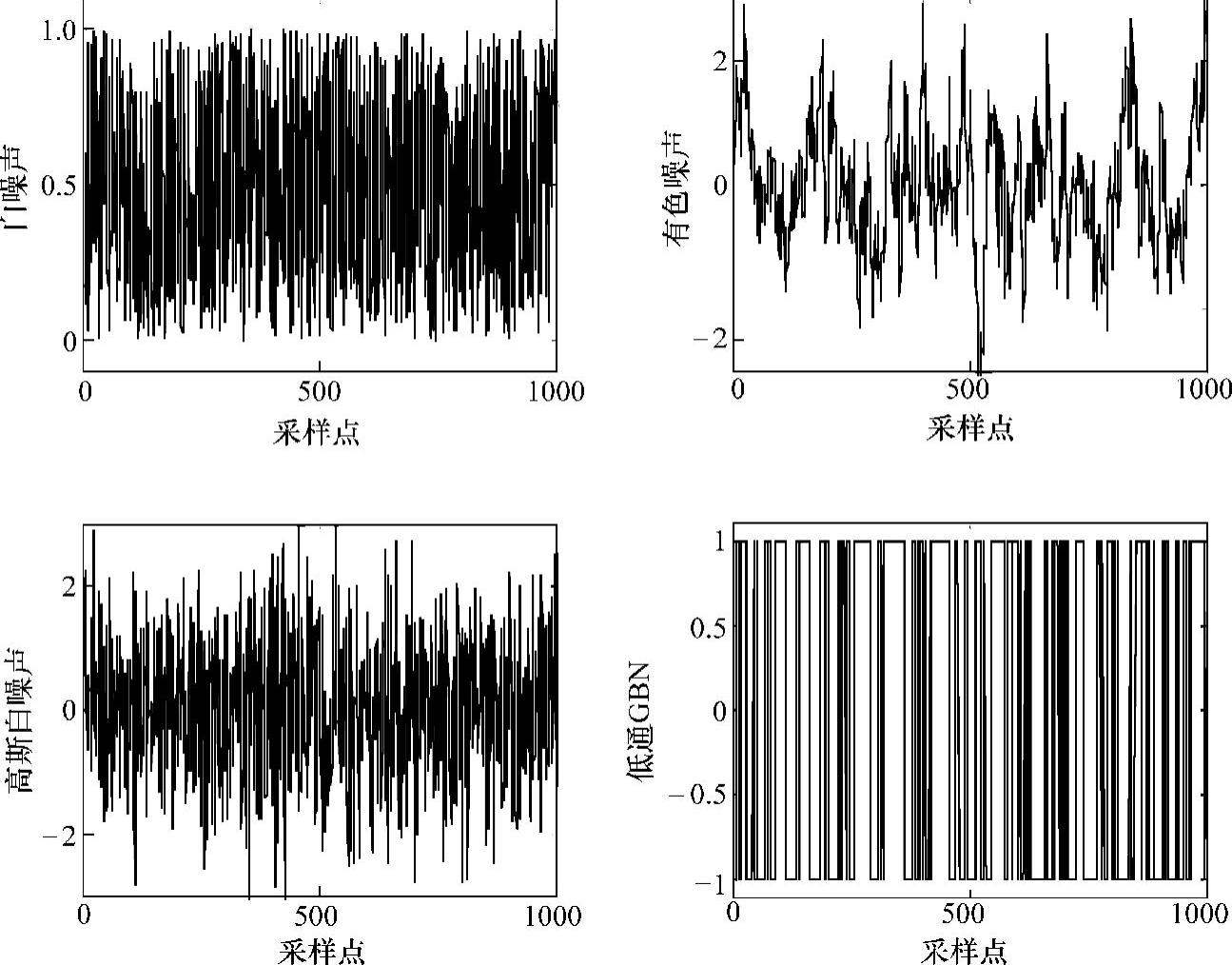
图10-2 不同白噪声信号模拟

3.伪随机信号PRBS

伪随机二位式序列的自相关函数接近于δ函数，其可以通过图10-3所示的反馈移位寄存器产生。图中Ꮞ表示模2加，a_i（i=0，2，…，n-1）表示寄存器，其可以有0或1两种状态，且初始状态不能全为零。当施加时钟脉冲，则第i个寄存器状态右移到第i+1个寄存器中，第一个寄存器则由反馈路径决定。PRBS的最大周期为M=2ⁿ-1，n为寄存器个数，周期为M的PRBS称为最大长度PRBS或M序列。实际应用中可适当选择循环周期、脉冲宽度和信号幅值。

图10-3 移位寄存器产生PRBS结构图

图10-4所示为利用移位寄存器原理产生的PRBS序列，这里取n=6即周期M=2⁶-1=63。

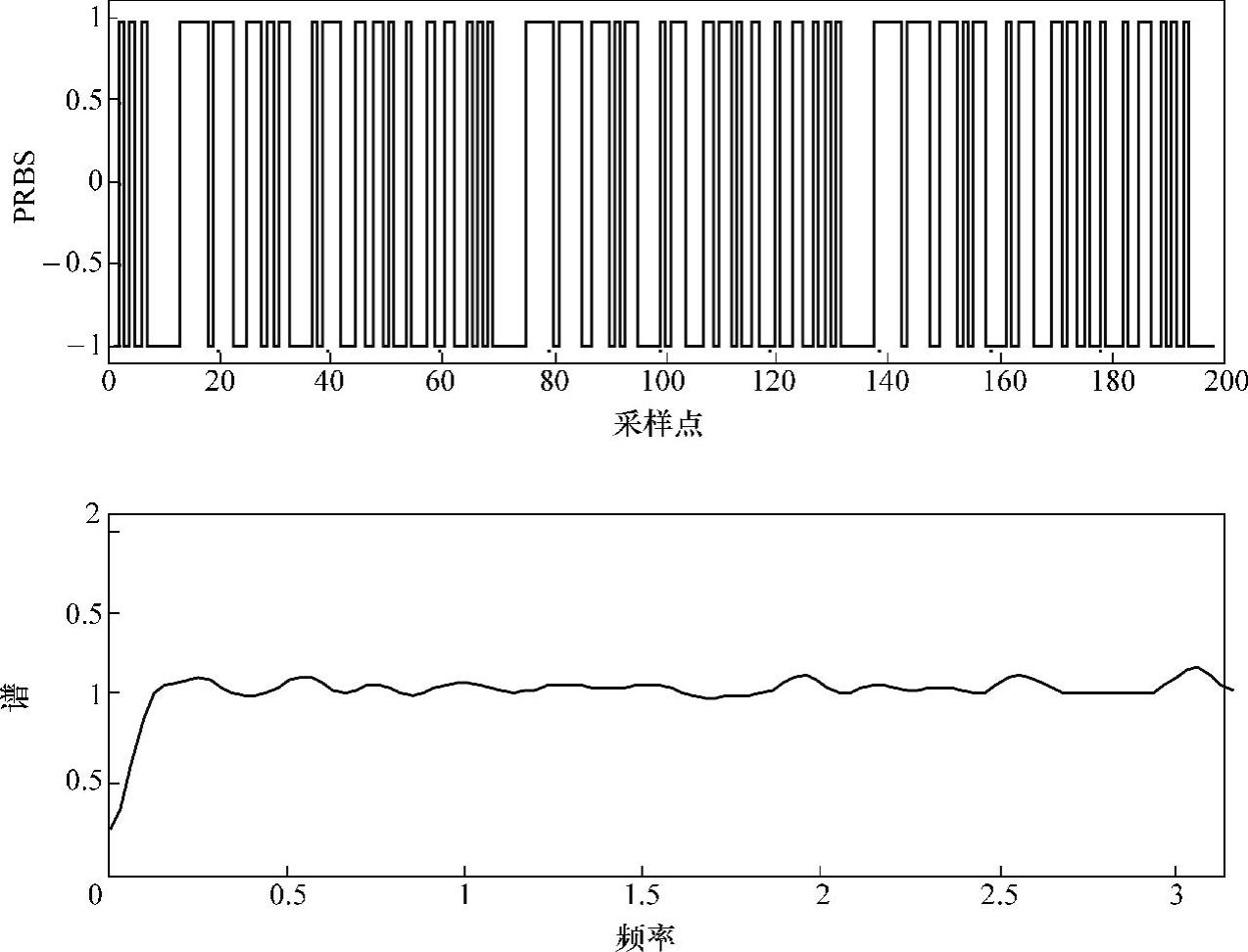
图10-4 伪随机信号模拟

通过实验测试收集的数据可能存在各种缺陷，如高频测量噪声、偶然出现的脉冲和无效值、偶然出现的不可测扰动使系统超出线性范围、工作点的转变引起的非线性、漂移和失调。因此，需要做一些数据预处理，常用的处理方法：①废值的剔除和补正；②信号限幅；③数据平滑；④数字低通滤波；⑤缩放及去偏校正；⑥趋势校正或高通滤波；⑦延迟校正；⑧非线性模型辨识预处理。