【摘要】：首先利用误差转换的设计方法来优化系统的动态特性，包括调整系统的收敛时间、超调量和稳态误差。误差转换的基本思想是当原始误差趋于指定的误差上下界时，转换后的误差将趋于无穷大。图8-1 转换函数示意图因此，由式（8-1）和式（8-2）可知，当转换误差s有界时，我们可以得到-ηφ＜e＜φ，即保证了原始功率跟踪误差始终在其用户设计的上下界中，也就保证了系统的稳态误差、收敛速度、超调量等动态指标。
首先利用误差转换的设计方法来优化系统的动态特性，包括调整系统的收敛时间、超调量和稳态误差。误差转换的基本思想是当原始误差趋于指定的误差上下界时，转换后的误差将趋于无穷大。同理，如果我们可以保证转换误差是一个有界信号，也就可以保证原始误差不超过指定的误差界，也就保证了风力发电机组跟踪最优功率曲线的动态特性。
假设实际风能功率输出和理想最优功率输出之间的原始误差表示为e（t），转换误差为s（t）。如果我们设计的误差上界为φ（t），误差下界为-ηφ（t），则动态特性与误差上下界的关系可以确定如下：①系统的稳态跟踪误差e（∞）满足-ηφ（∞）≤e（∞）≤φ（∞）；②系统的收敛时间大于上界的收敛速度；③系统的超调量小于ηφ（0）。因此，我们设计转换误差s（t）与原始误差e（t）的关系为
e（t）=φ（t）M（s） （8-1）
其中，M（s）是用户自定义的单调递增且可逆的光滑函数，M（s）满足
(www.xing528.com)
图8-1所示为转换函数M（s）的示意图。
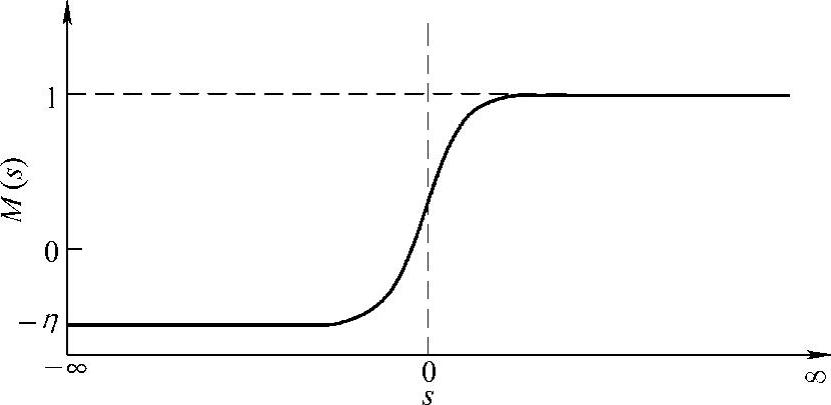
图8-1 转换函数示意图
因此，由式（8-1）和式（8-2）可知，当转换误差s（t）有界时，我们可以得到-ηφ（t）＜e（t）＜φ（t），即保证了原始功率跟踪误差始终在其用户设计的上下界中，也就保证了系统的稳态误差、收敛速度、超调量等动态指标。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
