独立变桨控制实现方案：采用LQG控制器

线性二次型最优控制（LQG）是现代控制理论最重要的应用成果之一，应用十分广泛，求解简单。线性二次型最优控制问题（LQG）用于具有二次性能指标函数和高斯分布白噪音干扰的随机系统，可以利用分离原理把最优控制问题和状态变量的最优估计问题分开来研究。LQG控制器设计步骤为：先假定状态变量已经得到，然后用最优控制方法解出最优控制。在用卡尔曼滤波估计状态，把估计的状态变量带入最优方程，进而实现最优控制。

大型风电机组独立变桨控制系统线性化后的状态空间方程为[20]

式中 x——状态矢量，指的是风轮面内、面外1-6阶的位移、速率，塔架前后、左右1-2阶的位移、速率；

u——控制矢量，指的是d轴桨距角要求β^cm₂和q轴桨距角要求β^cm₃；

y——输出矢量，指的是d轴载荷M_d和q轴载荷M_q；

A——系统矩阵；

B——输入矩阵；

C——输出矩阵；

D——直接传递矩阵。

上述状态空间方程的离散化，即可以得到离散状态空间方程表达式：

x（k+1）=Gx（k）+hu（k）

y（k）=C^Tx（k）+du（k） （7-51）

图7-34和图7-35分别为基于LQG的独立变控制原理框图和LQG控制器结构原理图。如图所示，考虑系统存在高斯分布白噪音干扰的随机系统，用卡尔曼滤波估计出状态矢量x（k）：

x（k）=x′（k）+M（y′（k-1）-y（k-1）） （7-52）

式中 y′——预测的输出矢量；(www.xing528.com)

x′——预测的状态矢量；

y——测量得到输出变量；

M——卡尔曼滤波增益矩阵。

建立系统二次性性能泛函：

J=x^TPx+u^TQu （7-53）

式中 P——半正定的状态加权矩阵；

Q——正定的控制加权矩阵，系统最优控制目标就是使J最小，并得到u控制矢量（指的是d轴桨距角要求β^cm₂和q轴桨距角要求β^cm₃计算公式：

u（k）=-Gx（k） （7-54）

式中 G——最优控制增益矩阵。

利用Matlab软件的线性化分析工具，得到卡尔曼滤波增益矩阵M和最优控制增益矩阵G。

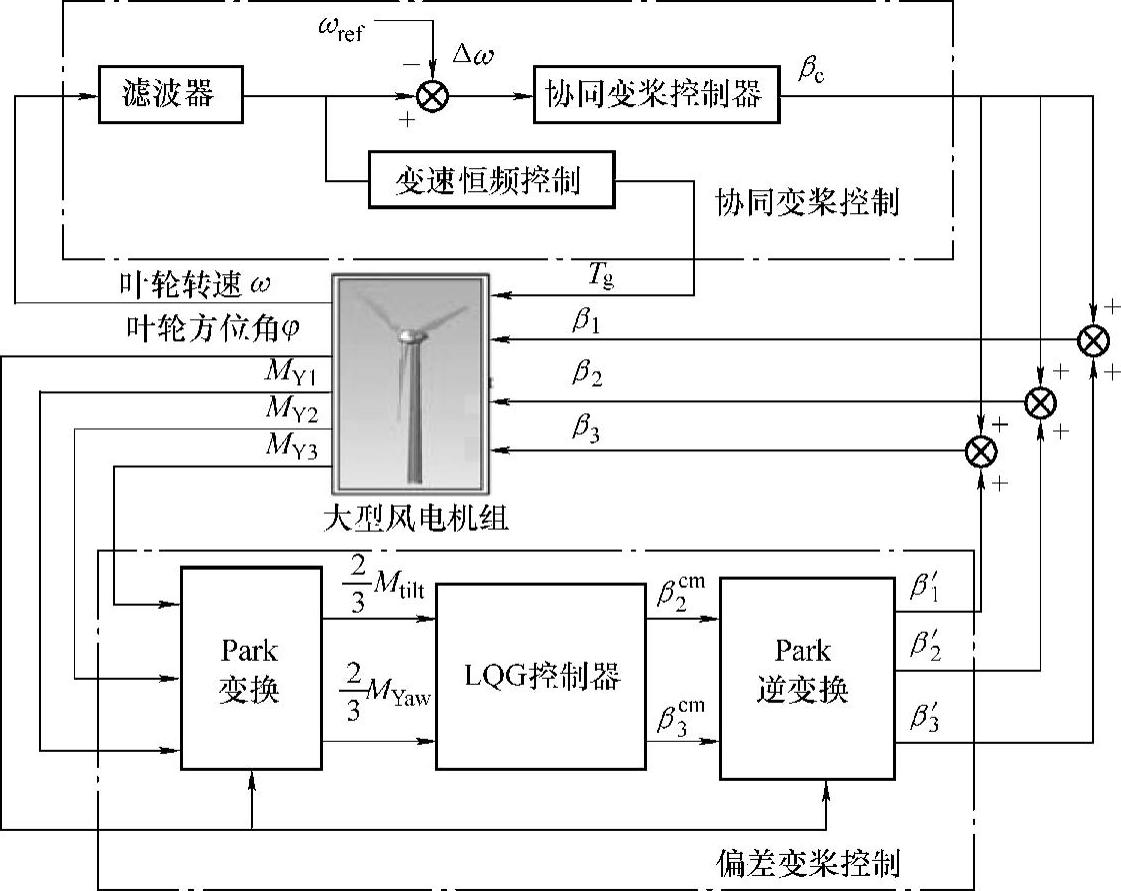
图7-34 基于LQG控制独立变桨控制原理框图

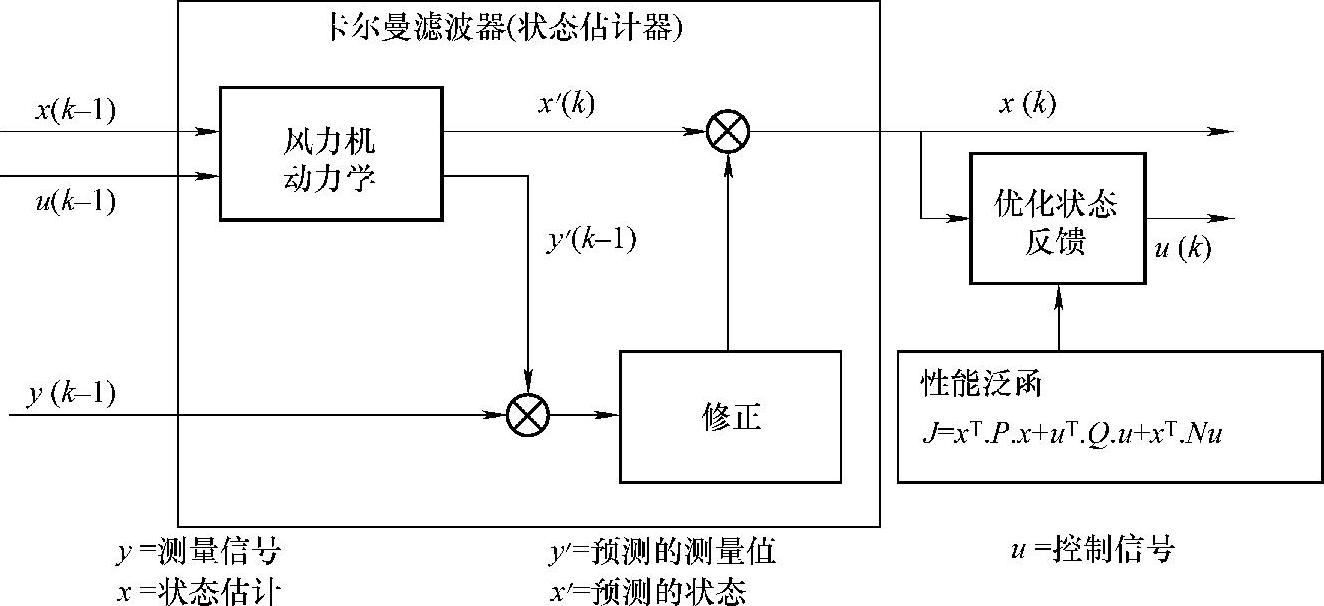
图7-35 LQG控制器结构原理图