P谐波控制理论分析

通过对风力机简化模型分析，推导出风力机的运动方程和输出方程，并通过Park坐标变换把塔架前后运动方程和载荷输出方程所代表的线性时变系统解耦为线性时不变系统，并根据式（7-17）、式（7-20）和式（7-21）分别设计出独立变桨控制器的转速控制环、倾覆力矩控制环、偏航力矩控制环。下面在频域上对独立变桨控制策略进行分析。

通过Park坐标变换可以实现风轮旋转坐标系与轮毂固定坐标系之间的变量变换，且有：

不考虑塔架前后运动对倾覆力矩的影响，同时考虑到变桨动作的滞后，公式（7-20）（7-21）变成：

式中：τ为载荷测量、控制器处理、变桨机构执行引起的滞后时间。

分析式（7-24）、式（7-25），k_MZ、h_MZ是在工作点附近线性化处理后的系数，u^cm₂、u^cm₃是干扰输入，因此式（7-24）、式（7-25）分别代表单输入单输出的线性系统，因此载荷控制器的设计原理是：在干扰输入u^cm₂、u^cm₃作用下，通过对M^cm_Y2、M^cm_Y3的反馈，经PI控制器调节β₂^cm、β₃^cm，使M^cm_Y2、M^cm_Y3最小。

假定风轮面积内风速湍流是均匀的，则叶片上等效风速u_i的傅里叶级数为(www.xing528.com)

其中，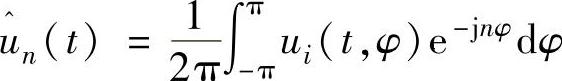

把式（7-26）代入式（7-14）得

分析式（7-27）中的u^cm₁等式和式（7-17）可知道，在转速控制环中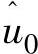，（t）（即0P）谐波分量是直接转换为u^cm₁，与方位角φ无关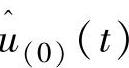，谐波分量主要由均匀湍流风速引起的（不含风剪切、塔影效应），因此通过PI控制器可以很好控制低频风速引起的转速变换（减小均值）。为了减小高谐波分量影响，因此设计转速控制环时，需要设计低通滤波器或者加入适当的转矩控制。而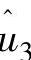、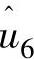…谐波分量（3P、6P，…谐波）会变换为关于φ时变的u^cm₁，这些谐波分量主要是由风剪切、塔影效应等因素所引起的，转速控制环不需要对这些谐波分量响应（因为对这些谐波分量的响应会导致过多无效的变桨动作，会加快变桨机构的磨损），因此需要设计滤波器滤掉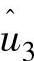、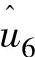，…分量，但由于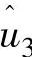、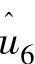，…谐波分量衰减较快，一般只考虑过滤3P和6P谐波。

在分析式（7-27）中的u^cm₂、u^cm₃等式可知道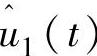，（即1P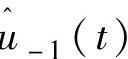，没有物理意义，不考虑）谐波分量是直接转换为u^cm₂和u^cm₃，即与u^cm₂和u^cm₃成比例，与方位角φ无关，即转换为0P谐波分量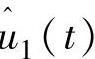，谐波分量主要是由风剪切、塔影效应等因素所引起的。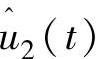、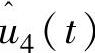（即2P和4P）谐波分量变换为u^cm₂和u^cm3的3P谐波分量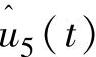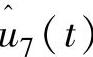，、（即5P和6P）谐波分量变换为u^cm₂和u^cm₃的6P谐波分量。通过载荷控制环的PI控制，可以有效补偿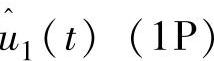风速引起的载荷（0P谐波分量）变化，因此这种载荷控制称1P控制。为了减小高谐波分量影响，因此设计转速控制环时，需要设计低通滤波器，截止频率一般小于3P。