独立变桨控制既要实现功率控制,又要实现载荷控制(减小风轮上不均衡载荷),因此需对风力机运行工况和载荷工况进行分析。为了便于分析,对风力机模型进行线性简化处理,其包括以下特征:
1)独立变桨控制的刚性叶片;
2)传动链一阶扭转模型;
3)一阶塔架前后弯曲模型;
4)发电机转矩控制。
1.风轮模型线性化处理
本章采用的坐标系如图7-2所示。忽略尾流效应和不稳定的空气动力学特性,假定轮毂为0。在风轮旋转坐标系上,叶根坐标系和风轮旋转坐标系为一个坐标系,根据叶素理论可知,第i片桨叶根部上的面外方向(out of plane)力和力矩、面内方向(in plane)的力和力矩与叶片面外方向的相对有效风速vfli及节距角βi关系式为
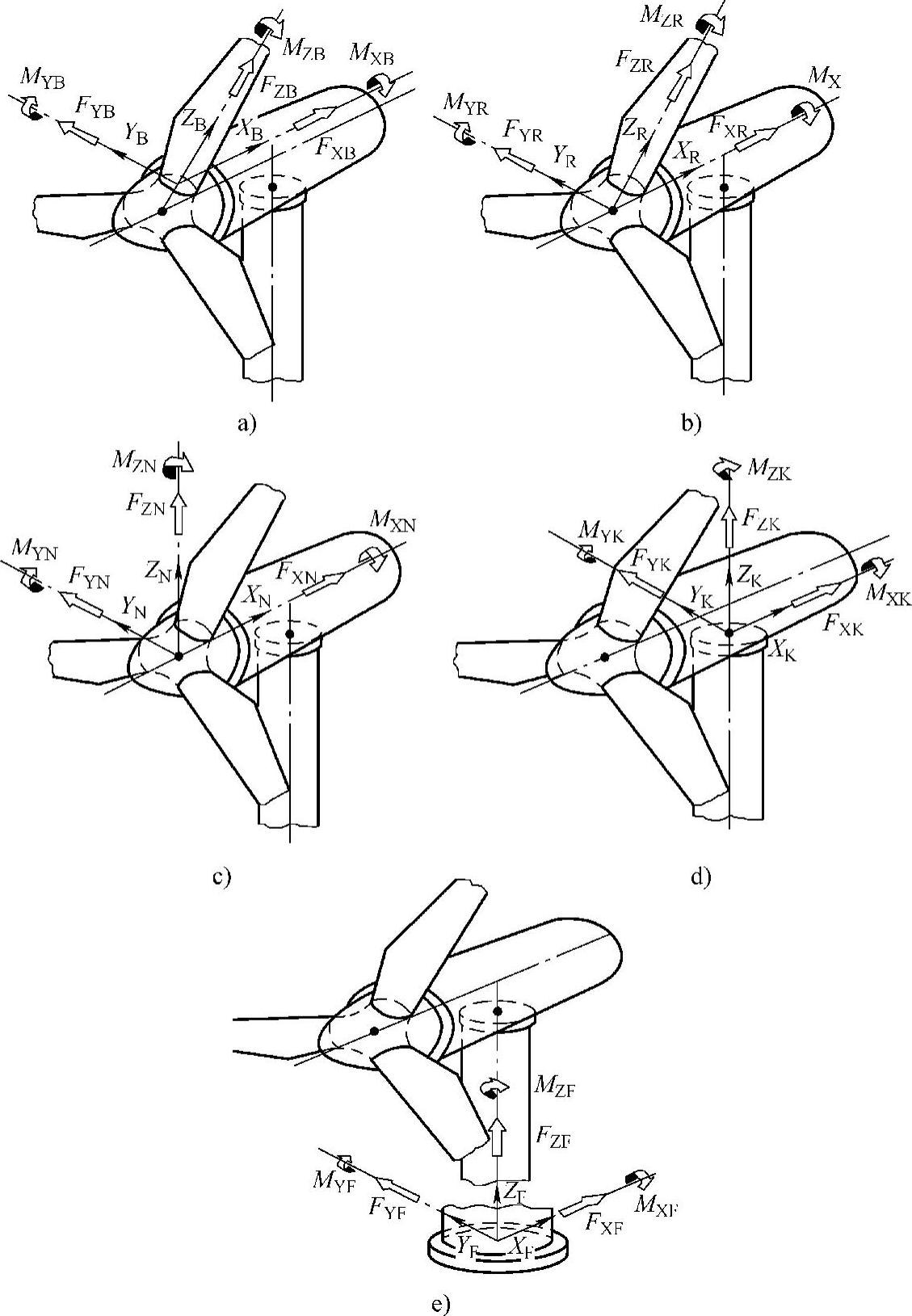
图7-2 风电机组坐标系定义
a)桨叶根部坐标系 b)风轮旋转坐标系 c)轮毂固定坐标系 d)塔顶坐标系 e)塔底坐标系
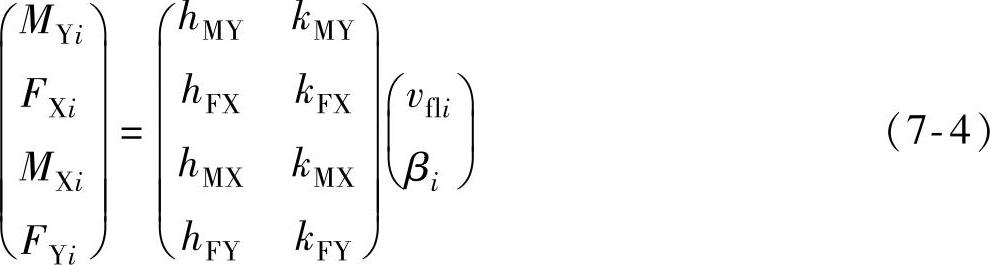
式中 i——第i片桨叶,i=1,2,3;
MYi、FXi——分别为第i叶片根部上的面外方向的力矩和力;
MXi、FYi——分别为第i叶片根部上的面内方向的力矩和力;
hMY、hFX、hMX、hFY、kMY、kFX、kMX、kFY——分别是工作点附近线性化处理后的系数(其中,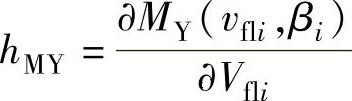 ,
,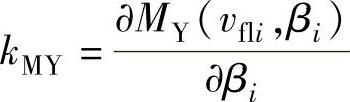 ;h
;h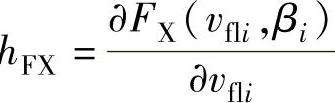 ,
,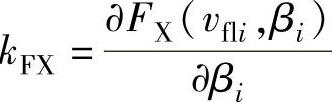
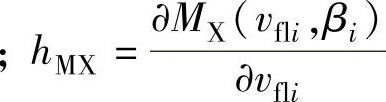
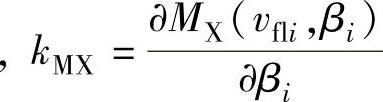 ;
;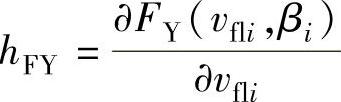 ,
,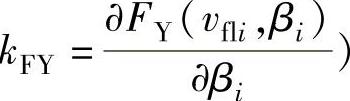 。
。
在轮毂固定坐标系上(见图7-2c),风轮的气动力矩MX,轴向力FX,倾覆力矩Mtilt(即轮毂固定坐标系上的MY),偏航力矩MYaw(即轮毂固定坐标系上的MZ)分别为
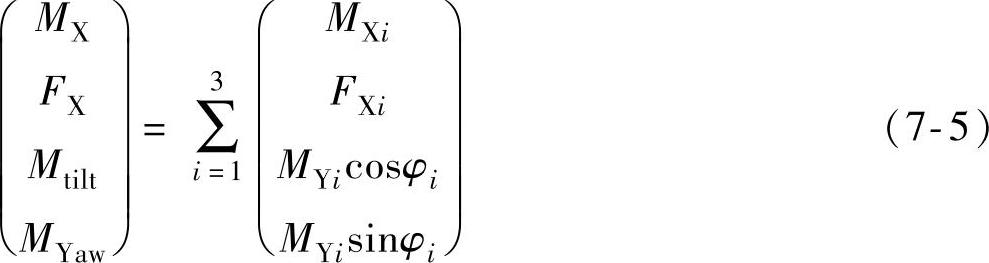
其中,φi为第i片桨叶的方位角。假定风轮方位角φ等于第一片桨叶的方位角,则φ1=φ,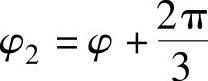 ,
,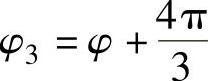 。
。
叶片面外方向的相对有效风速vfli由叶片上等效风速ui与塔架前后运行引起的相对风速组成,vfli为
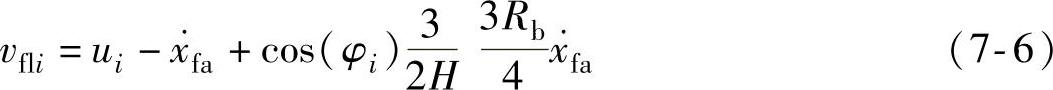
式中 xfa——塔架顶部前后方向位移;
Rb——风轮半径;
H——塔架高度。
根据式(7-4)和式(7-5)代入式(7-6)得
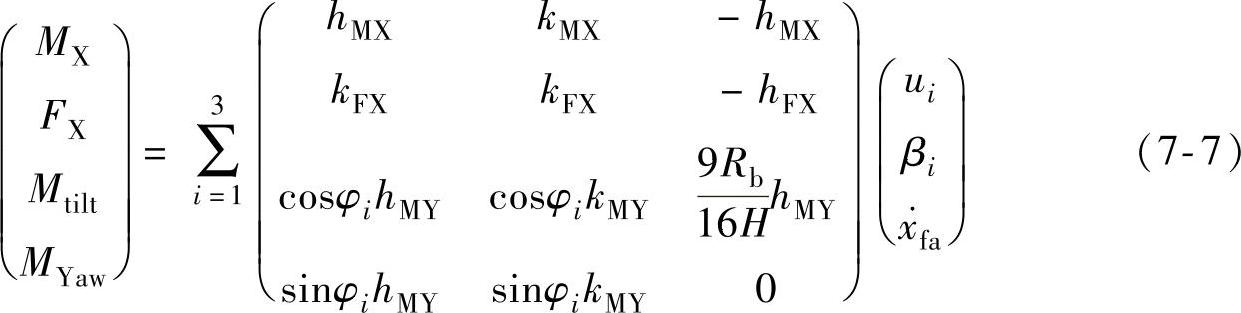
2.运动方程
考虑系统的柔度,把主轴、齿轮箱传动系统的各部分惯量折算到风轮上,且将主轴、齿箱传动的柔度等效到齿箱输出轴上,因此传动链的运行方程为

式中 ω——风轮转速;(https://www.xing528.com)
J=Jr+n21J1+…+n2nJn——风轮及传动系统折算到风轮上的转动惯量;
n1、n2、…、nn,J1、J2、…、Jn——传动系统各级传动比及相应转动惯量;
B——等效阻尼系数;
Tg——发电机转矩。
塔架前后方向的运行方程为
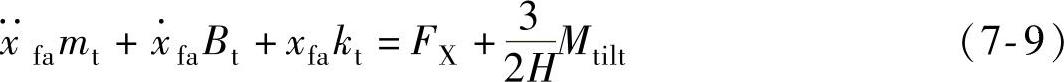
式中 mt——塔架等效质量;
Bt——塔架等效阻尼;
kt——塔架等效弹性系数。
把式(7-4)带入式(7-5)和式(7-6)得出传动链和塔架的运行方程为
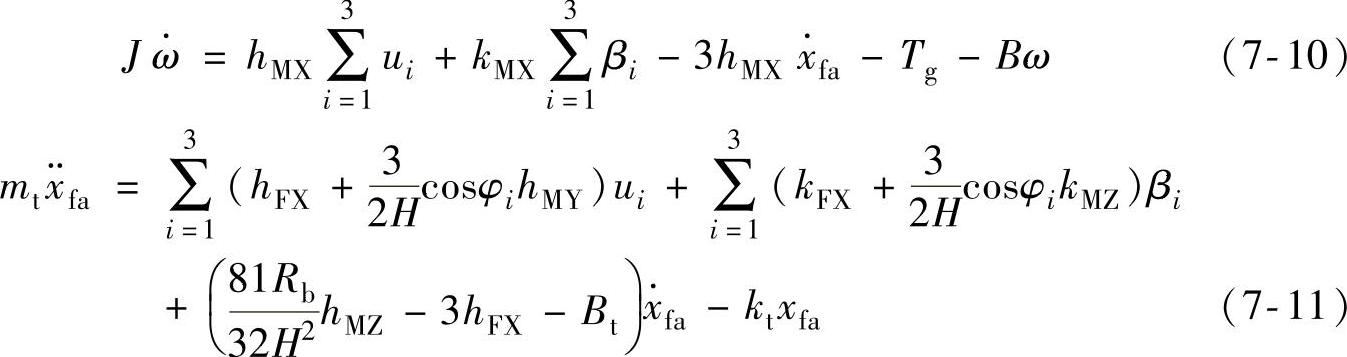
3.输出方程
由经典控制理论可知,选取不同的反馈控制变量则有不同的输出方程,独立变桨控制可以选择叶片根部面外弯曲力矩、主轴的弯曲力矩、机舱的倾斜力矩和偏航力矩、塔顶的力矩等作为反馈变量。一般都选取叶片根部面外弯曲力矩作为反馈变量,其输出方程为
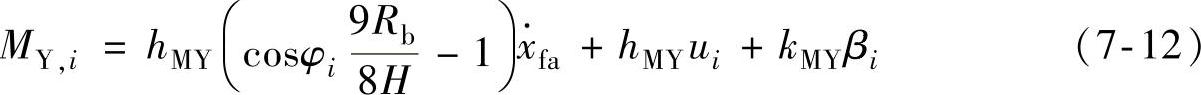
4.坐标变换
由式(7-11)和式(7-12)可知,塔架运行方程和输出方程是关于风轮方位角φ的线性时变方程,可以参照电机学矢量控制中常用的坐标变换,将塔架运行方程和输出方程变换为关于风轮方位角φ的线性时不变方程。选用的坐标变换又称Park坐标变换,其物理意义是实现风轮旋转坐标系与轮毂固定坐标系之间的变量变换。
所采用Park坐标变换矩阵P和逆矩阵P-1分别为
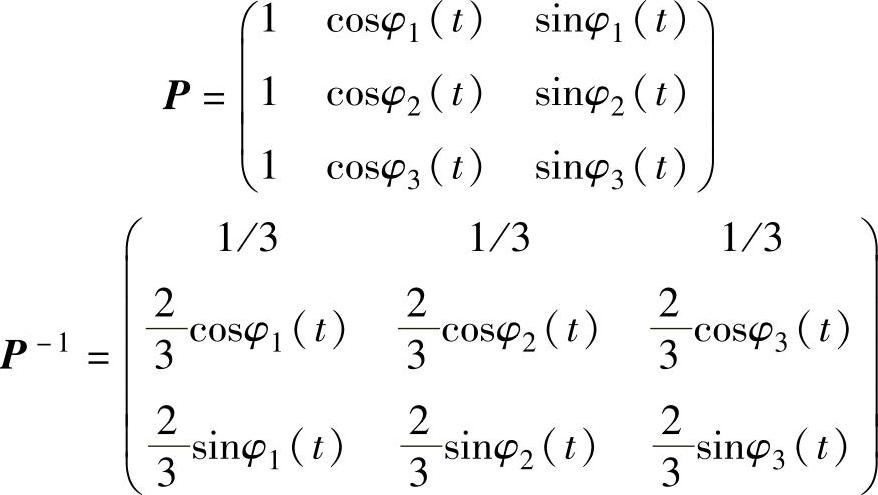
将各叶片的节距角βi、等效风速ui、根部面外弯曲力矩MYi变换到轮毂固定坐标系上:
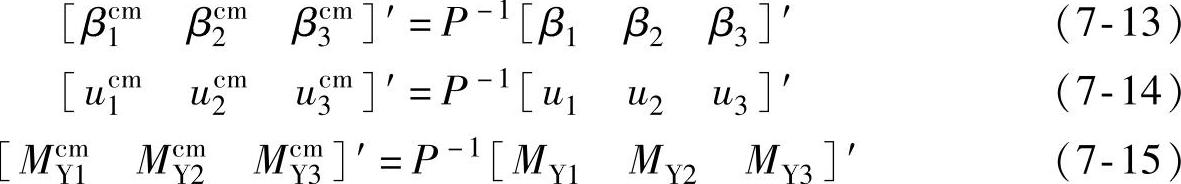
其中,βcmi、ucmi、McmYi分别为变换到轮毂固定坐标系上的节距角、风速、面外弯曲力矩分量。
由图7-2与式(7-5)和式(7-15)分析可知,轮毂固定坐标系上McmY2、McmY3分量有其物理意义,其值分别与轮毂倾覆力矩Mtilt和偏航力矩MYaw成比例,且有

5.线性时不变方程
把式(7-13)~式(7-16)代入式(7-10)~式(7-12)得出下列关于风轮方位角φ的线性时不变方程:
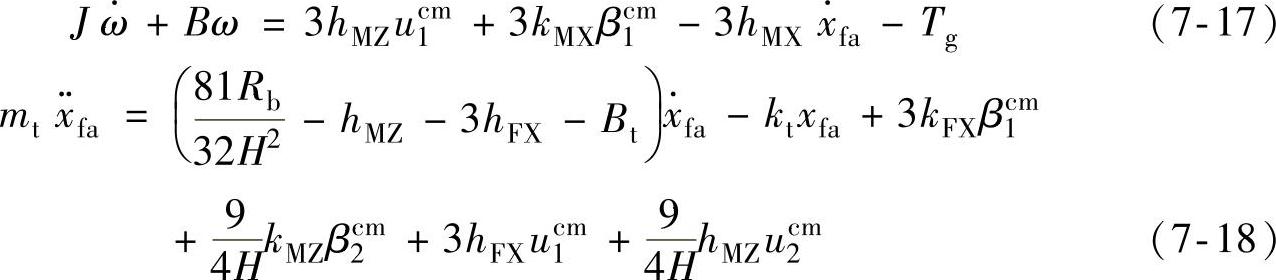
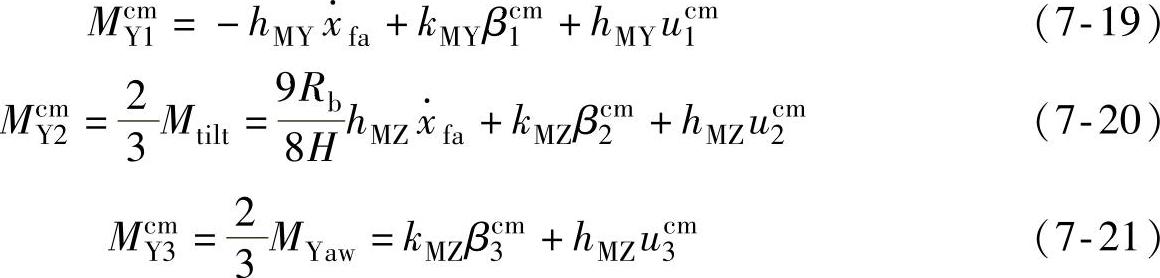
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




