如何将连续系统离散化？

由于计算机实时控制过程中采样信号的离散性，设计控制系统时最终要将连续条件下设计的控制系统离散化（见图6-5）。

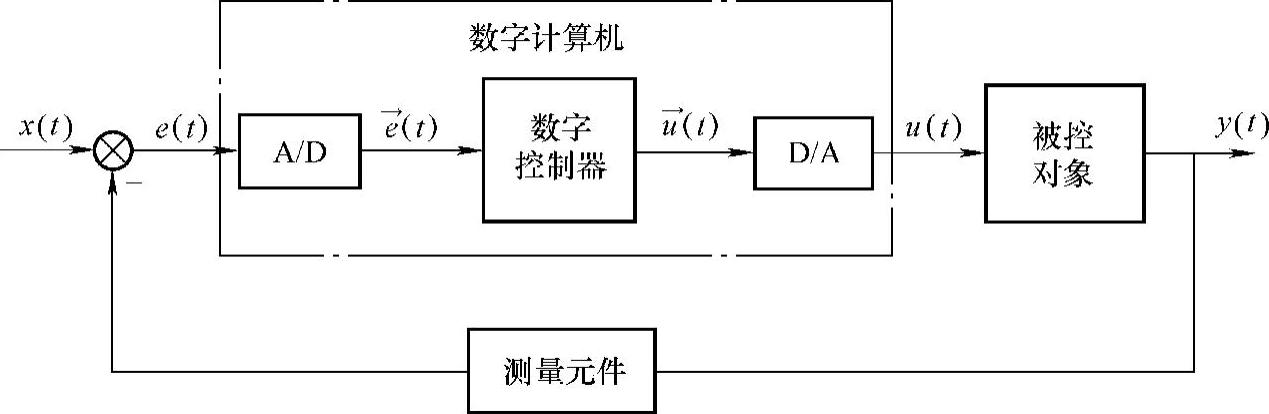
图6-5 数字控制系统原理结构图

采样可能发生在系统的一个或多个位置，在框图中采样操作可被表示为开关符号，如图6-6所示。

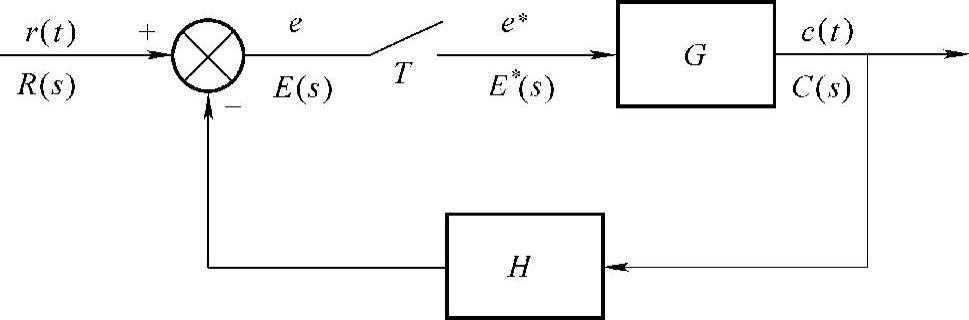
图6-6 包含实际采样信号的采样数据控制系统框图

图6-6中，带有星号的变换表示经过周期为T的序列脉冲的采样。该系统方程为

C（s）=G（s）E^∗（s） （6-33）

E（s）=R（s）-B（s）=R（s）-G（s）H（s）E^∗（s） （6-34）

式（6-34）的星变换为

E^∗（s）=R^∗（s）-GH^∗（s）E^∗（s） （6-35）

将式（6-35）的结果代入式（6-33），有

式（6-36）的星变换为(www.xing528.com)

于是，可将式（6-37）改写为离散形式，即

除上述方法外，还可以采用双线性变换法实现s到z平面的变换，其原理为以z表示s，产生z的函数，进而得到这种变换的线性近似，即

将自然对数lnz展开成级数为

式中

仅使用式（6-40）的第一项，产生双线性变换，有

s的表达式能够插入到一个函数中，如G（s），它代表一个连续时间函数，将表达式有理化，就产生函数G（z），它代表一个离散函数。

双线性变换法的一个优势是相对容易实现，相比于精确z域传递函数的响应来说，双线性变换法的z域传递函数响应的精度要好，即随频率增加，精度也增加。