风电机组线性化模型的优化方法

风电机组控制系统的设计和分析方法都涵盖在经典控制理论范围内，所面对的控制对象是一个多输入-多输出的非线性时变系统。为此，在进行控制系统设计前需要对风电机组动态模型进行线性化。

（一）线性系统和非线性系统

线性系统即可以用线性微分方程描述的系统。如果方程的系数为常数，则为线性定常系统；如果方程的系数是时间t的函数，则为线性时变系统。

线性是指系统满足叠加原理，即

可加性：f（x₁+x₂）=f（x₁）+f（x₂）

齐次性：f（αx）=αf（x）

非线性系统即用非线性微分方程描述的系统。非线性系统不满足叠加原理。实际的系统通常都是非线性的，线性只在一定的工作范围内成立。为分析方便，通常在合理的条件下，将非线性系统简化为线性系统处理。

线性系统微分方程的一般形式为

式中，a₁，a₂，…，a_n和b₀，b₁，…，b_m为由系统结构决定的实常数，m≤n。

（二）非线性模型的线性化

由于非线性系统的分析和处理是非常复杂的，而实际系统在一定的工作范围内具有线性特性，因此可以在局部范围内采用线性化模型近似代替非线性模型进行处理。

对于一个非线性系统，可以用泰勒级数展开法进行线性化。

函数y=f（x）在其平衡点（x₀，y₀）附近的泰勒级数展开式为(www.xing528.com)

略去含有高于一次的增量Δx=x-x₀，则

或

y-y₀=Δy=KΔx （6-4）

式中，。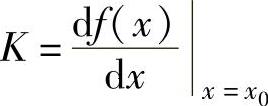

式（6-4）即为非线性系统的线性化模型，称为增量方程。y₀=f（x₀）称为系统的静态方程。

对于多变量系统，如y=f（x₁，x₂），同样可以采用泰勒级数展开获得线性化的增量方程。

增量方程为

y-y₀=Δy=K₁Δx₁+K₂Δx₂ （6-6）

静态方程为

y₀=f（x₁₀，x₂₀） （6-7）

式中，；。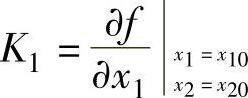

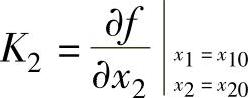对于风电机组这样的复杂多变量系统，机组本身的模型线性化是可以由建模工具软件（如Bladed、FASTAD、FLEX5）来完成的。