【摘要】:(二)第二个方法应用气动的一般理论确定dFa和dT。今研究气流通过一段环形面积的轴向动量,则推力dFa等于单位质量流量m穿过环形面时与速度变化的乘积,即dFa=mΔv=m因 m=ρ2πvrdr=ρπrdr(1+k)v1有 dFa=ρπv2rdr 同样,若考虑到角动量的关系,可得到转矩dT:dT=mΔωr2=mr2Ω式中 Δω──气流通过螺旋桨时的变化,Δω=Ω。
今研究(r,r+dr)段叶片的受力情况,可采用两种方法。
(一)第一个方法
由式(2-37)和式(2-38)知
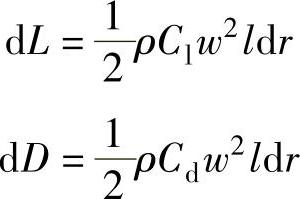
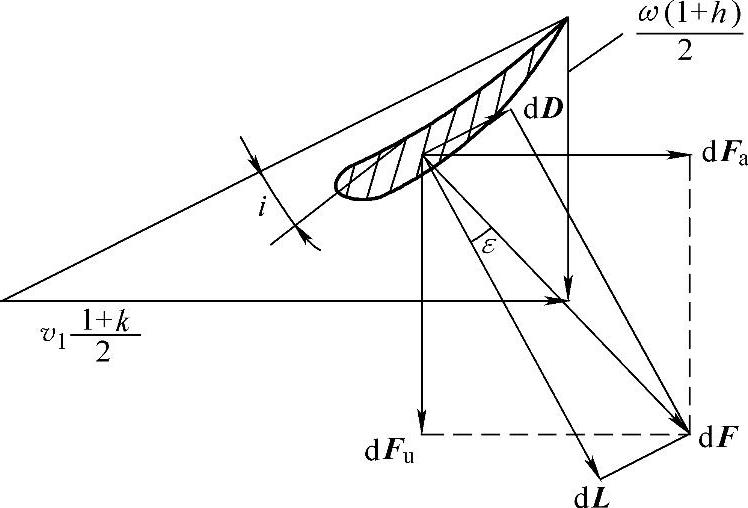
图2-14 考虑诱导速度的叶素特性分析
分别将dL和dD的合力dF投影到转轴和圆周速度u上,得到(图2-14):
轴向分量:
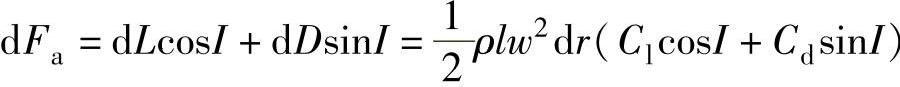
切向分量:
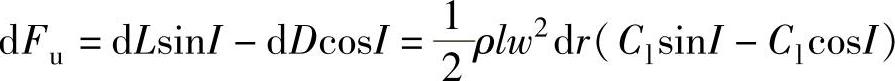
引入关系式tanε=Cd/Cl,则上述方程可写成:
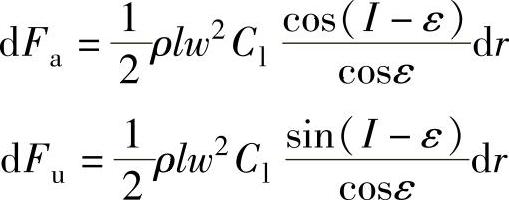
于是,(r,r+dr)段叶片的轴向推力为
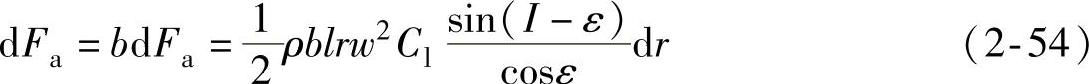
气动转矩为
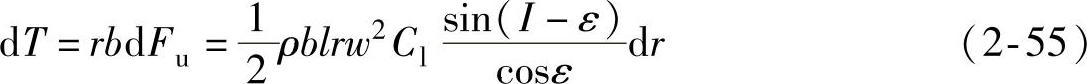
将式(2-54)和式(2-55)与简化的风力机理论第二种方法对比可以看出,当不计及诱导速度的影响时,两者是一致的。
(二)第二个方法
应用气动的一般理论确定dFa和dT。(https://www.xing528.com)
今研究气流通过(r,r+dr)一段环形面积的轴向动量,则推力dFa等于单位质量流量m穿过环形面时与速度变化的乘积,即
dFa=mΔv=m(v1-v2)
因 m=ρ2πvrdr=ρπrdr(1+k)v1
有 dFa=ρπv2rdr(1-k2) (2-56)
同样,若考虑到角动量的关系,可得到转矩dT:
dT=mΔωr2=mr2Ω
式中 Δω──气流通过螺旋桨时的变化,Δω=Ω。
则 dT=ρπv1r3dr(1+k)Ω
或 dT=ρπr3drωv1(1+k)(h-1) (2-57)
(三)结果
对比上述两种dFa等式,然后替换w,令w为v1的函数,则
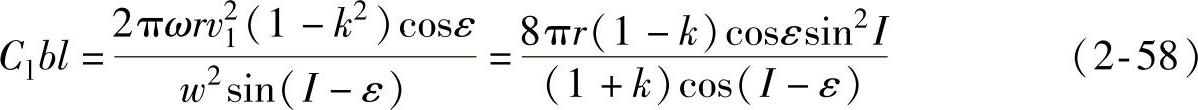
用同样方式,对比dT的等式可得
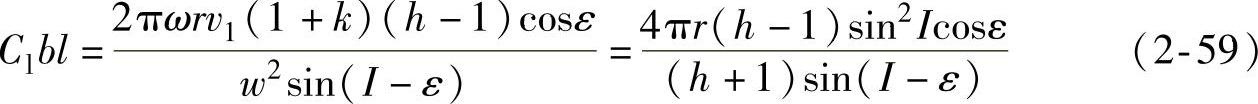
由这些方程式经某些变换后,可得到下列形式:
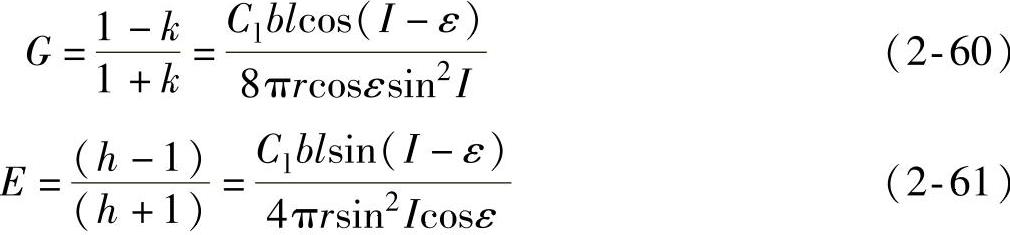
式中G和E为计算过程中采用的简化符号。这两个公式建立了风轮的几何参数、气动参数与速度因子之间的关系。
两式相除后,得
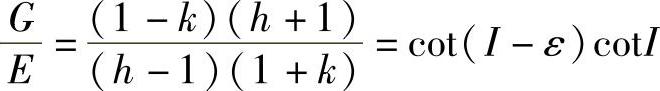
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




