作用在运动桨叶上的气动力分析与应用技巧

假定桨叶处于静止状态，令空气以相同的相对速度吹向叶片时，作用在桨叶上的气动力将不改变其大小。气动力只取决于相对速度和攻角的大小。因此，为便于研究，均假定桨叶静止处于均匀来流速度v中。

此时，作用在桨叶表面上的空气压力是不均匀的，上表面压力减少，下表面压力增加。

按照伯努利理论，桨叶上表面的气流速度较高，下表面的气流速度则比来流低。因此，围绕桨叶的流动可看成由两个不同的流动组合而成：一个是将叶型置于均匀流场中时围绕桨叶的零升力流动；另一个是空气环绕桨叶表面的流动。而桨叶升力则由于在桨叶表面上存在一速度环量，如图2-3所示。

图2-3 气流绕桨叶的流动

为了表示压力沿表面的变化，可作桨叶表面的垂线，用垂线的长度K_p表示各部分压力的大小：

式中 p──桨叶表面上的静压；

ρ、p₀、v──无限远处的来流条件。

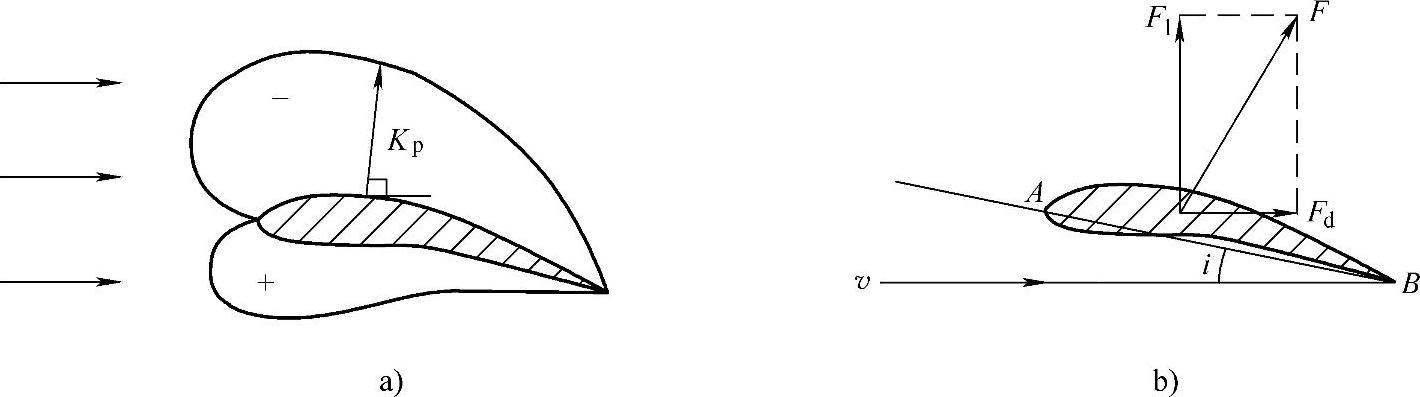
连接各垂直线段长度K_p的端点，得到图2-4a，其中上表面K_p为负，下表面K_p为正。

使用在桨叶上的力F与相对速度的方向有关，并可用下式表示

式中 S──桨叶面积，等于弦长×桨叶长度；

C_r──总的气动系数。

该力可分为两部分：分量F_d与速度v平行，称为阻力；分量F_l与速度v垂直，称为升力。

(www.xing528.com)

图2-4 作用在桨叶上的力

F_d与F_l可分别表示为

式中 C_d──阻力系数；

C_l──升力系数。

因两个分量是垂直的，故可写成：

F²_d+F²_l=F²

C²_d+C²_l=C²_r

若令M为相对于前缘点的由F力引起的力矩，则可求得变距力矩系数C_M。

式中 l──弦长。

因此，作用在桨叶截面上的气动力可表示为升力、阻力和变距力矩三部分。

由图2-4b可看出，对于各个攻角值，存在某一特别的C点，该点的气动力矩为零，称为压力中心。于是，作用在叶型截面上的气动力可表示为作用在压力中心上的升力和阻力。压力中心与前缘点之间的位置可用比值CP确定。

一般CP=（25～30）%。