空间直线的相对位置：平行、相交和交叉

空间两直线的相对位置有平行、相交和交叉三种。平行直线和相交直线都在同一平面上，称为共面直线，而交叉直线不在同一平面上，称为异面直线。

1.两直线平行

两直线平行，其同面投影必平行（除去投影重合情况），且两平行线段长度之比等于其投影长度之比。

如图3-16（a）所示，AB∥CD，投射线形成的平面ABba∥CDdc，它们与H面的交线互相平行，即ab∥cd。同理可证明a′b′∥c′d′，a″b″∥c″d″。

反之，若两直线的所有同面投影都互相平行，则此两直线必互相平行。

当两直线是一般位置时，只要有两对投影互相平行就可判定两直线平行，如图3-16（b）所示，若ab∥cd，a′b′∥c′d′，则必定a″b″∥c″d″，因此AB∥CD。

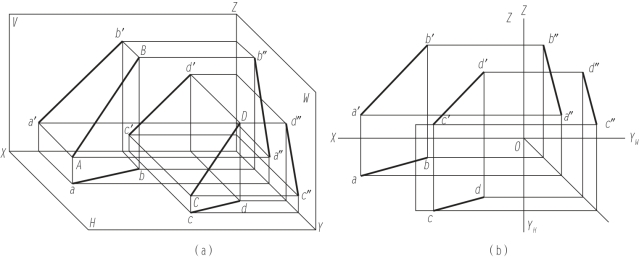
图3-16　平行两直线的投影

（a）立体图；（b）投影图

【提示】　当两平行直线为某投影面平行线时，应检查在该投影面上的投影是否相互平行。

2.两直线相交

两直线相交，其同面投影必相交，且交点的投影符合点的投影规律。如两直线都是一般位置直线，只要根据任意两面投影就可以判别两直线是否相交。

如图3-17所示，点K为直线AB与CD的共有点，它的投影必定同时在两直线的同面投影上，而且必符合空间点的投影规律，即kk′⊥OX，k′k″⊥OZ，kxk＝k″kz。(https://www.xing528.com)

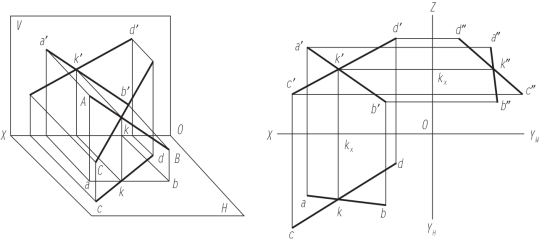
图3-17　相交两直线的投影

3.两直线交叉

既不平行又不相交的两直线称为交叉直线。它们的投影既不符合平行两直线的投影特点，又不符合相交两直线的投影特点。交叉两直线的同面投影可能表现为互相平行，但不可能所有同面投影都平行；它们的同面投影可能表现为相交，但交点的连线不垂直于投影轴。交叉两直线同面投影的交点是重影的投影。

如图3-18所示，AB线上的点Ⅲ与CD线上点Ⅳ是对H面的重影点，它们的H面投影重合，因点Ⅲ比点Ⅳ高，故点3可见，点4不可见。点Ⅰ与点Ⅱ是对V面的重影点，因点Ⅰ在Ⅱ的前面，故点1′可见，点2′不可见。

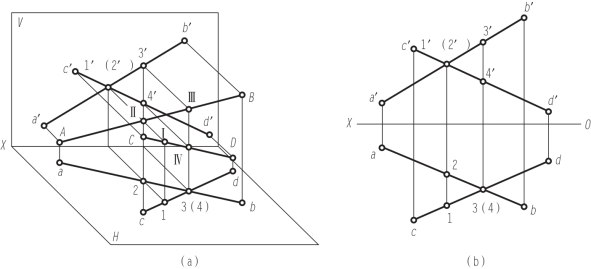
图3-18　交叉两直线的投影

【提示】　当交叉两直线的投影的交点为重影点时，应判别其可见性。

【例3-7】　如图3-19（a）所示，检验直线AB、CD的相对位置。

【解】　由于两直线的两组同面投影平行，不可能是相交，又因这两条直线上所有的点的x坐标分别相等，因而都是侧平线，可能互相平行，也可能交叉。先将已知条件的H、V两面投影体系扩展成三面投影体系，作出直线AB、CD的侧面投影a″b″、c″d″。由于a″b″与c″d″相交，则可检验出直线AB、CD交叉。作图过程如图3-19（b）所示。

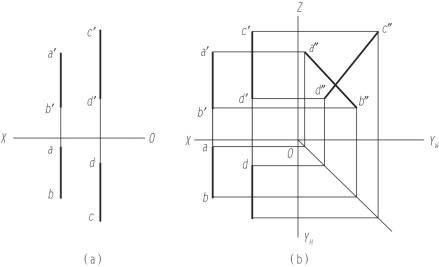
图3-19　检验两直线的相对位置

（a）已知条件；（b）作图过程及作图结果