优化GM1/GM2泵站的方案

GM1/GM2泵站的优化是两个泵站的联合优化过程，其限制条件是两个泵站运行的定速水泵的台数随时都应该相同，同时还要考虑申同嘴水库的动态情况。该优化模型的输入数据包括申同嘴水库的出水流量，该流量是通过GM3/SM1/SM2的优化计算而得的，输入数据还包括所有水泵的特性、效率和可利用率，同时还包括整个GM1/GM2系统的各种限制条件。在整个优化过程中，认为总有一台水泵是可以利用的。GM1/GM2的优化算法基于下面描述的动态编程。

本文件中的动态编程算法是由累计短缺流量对应时间的关系形成的，其中累计短缺流量ΔV是需求流量和流过泵站的流量之间的差额积分：

式中 ΔV——累计短缺流量，m3；

QPS——泵站通过流量，m3/s；

QS——需求流量，m3/s。

对于GM1和GM2泵站的优化，在优化时间段T内，累计短缺流量等于申同嘴水库的改变量。该改变量是预先定义好的，可以反映要求的水库容量总的变化，因此：

式中 ΔV S——预定的水库容量变化值，m3。

图6-2是关于短缺流量与时间的对应，可能出现的累计流量差额有下面4种限制条件：最大的多余抽水能力；没有水泵运行；水泵抽水流量的最大变化率；水库容积的限制。

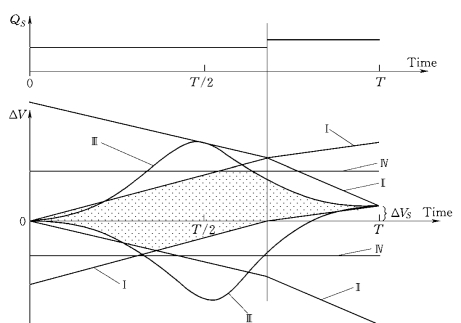
图6-2　累计流量差额对应时间和限制条件

对于GM1/GM2输水系统，不存在水泵抽水流量的最大变化率的限制。图中画点的区域为优化时间段T内可能累计的流量差额，即，必须在这个区域找出优化方案，在这个区域定义了一系列的离散点，各点的坐标表示为时间和累计短缺流量（t，ΔV）。每一点代表一种水泵的实际配置情况。水泵最小的累计能源消耗量包括开始点（0，0）到实际运行点（t，ΔV）以及相关的路径（点序列）。对所有路径，开始点和终端点都是相同的（0，0）和（T，ΔV S）。(www.xing528.com)

图6-3中示出了网格点阵，实线是到各网格点的最优路径，虚线是到各网格点可能的路径，需要进行计算。选择的路径应是累计能源消耗最小的路径。线路的坡度即为弃水流量。该坡度决定了ΔV的间距，而时间的间距是固定的。因为GM1和GM2只安装了定速水泵，该部分的优化运行不能灵活地采用网格中的流量，并受到由水头决定的流量的限制。

图6-3　网格点和最优路径

对GM1/GM2的优化，水泵的水头随着水库水位和流量的变化而变化。随流量变化是因为隧洞内的水头损失。从万家寨水库上游到申同嘴水库的总的水头损失应该以流量对应水头损失的图表形式输入模型。对应新的网格点，其最小累计能源消耗为：

式中 EΔVj，t+Δt——网格点j在时间t+Δt时的最小累计能源消耗量，J；

EΔVi，t——网格点i在时间t时的最小累计能源消耗量，J；

ΔEi→j——从网格点i到网格点j的最小累计能源消耗量，J；

ΔEi≠j——与启动额外水泵相关的能源消耗量，J。

当i确定后，该信息和最小能源消耗量一起保存在该网格点。

估算ΔEi→j要求对泵站进行再次优化，结果为：在规定的泵站抽水流量下相关泵站最小能耗之和。泵站再次优化将在给定的水头和流量下，得到最优的水泵选择和最佳的水泵转速。

对于GM1和GM2泵站，泵站的抽水流量将和定速水泵的台数相匹配，水泵根据其效率进行分配。泵站的抽水流量为离散点，其垂直位置必须和这些点的剩余流量（弃水量）相匹配。垂直网格点的间距应和1台水泵的（附加）抽水流量相匹配，这是（改变）水头的一个函数。因此网格横向间距（时间）是固定的，而垂直间距（ΔV）是变化的。注意：当规定的流量改变时，网格点垂直方向的位置也相应改变。

ΔEi≠j表示与启动额外水泵相关的能源消耗量，该数值应该作为模型的输入量。