卷积码编码过程及其电路设计

分组码在进行编码、译码时要把整个码组存储起来，处理时会产生较长的延时。卷积编码的码长n和信息码元个数k通常较小，故延时小，特别适合于以串行形式传输信息的场合。卷积编码（convolutional coding），又称卷积码，在任何一个码组中的监督码元不仅与本组的k个信息码元有关，而且与前面N-1段的信息码元有关。卷积码在N段内的若干码字之间加进了相关性，译码时不是根据单个码字而是一串码字来做判决。如果采用适当的编码、译码方法，就能够使噪声分摊到码字序列而不是一个码字上，达到噪声均化的目的。随着N的增加，卷积码的纠错能力增强，误码率则呈指数下降。

1.编码器

卷积码编码器由移位寄存器和加法器组成。输入移位寄存器有N段，每段有k级，共Nk位寄存器，负责存储每段的k个信息码元；各信息码元通过n个模2加法器相加，产生每个输出码组的n个码元，并寄存在一个n级的移位寄存器中移位输出。编码过程是输入信息序列与由移位寄存器和模2加法器之间连接所决定的另一个序列的卷积，因此称为卷积码。通常N称为卷积码的约束长度（constraint length）。卷积码用（n，k，N）表示，其中n为码长，k为码组中信息码元的个数，编码器每输入k比特，输出n比特，编码率为R=k/n。

约束长度不以码元数为单位而以分组为单位，这是因为编码和译码时分组数一定而相关码元数不同，编码时相关码元数是Nk，译码时相关码元数是Nn。显然以分组为单位来定义约束长度更方便。

图1-47为（2，1，3）卷积编码器的结构。图中没有画出延时为零的第一级移位寄存器，并用转换开关代替了输出移位寄存器。图1-47a中，M₁和M₂为移位寄存器，它们的起始状态均为零，即b_ib_i-1b_i-2为000。c₁，i和c₂，i与b_ib_i-1b_i-2的关系为

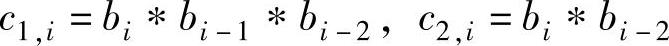
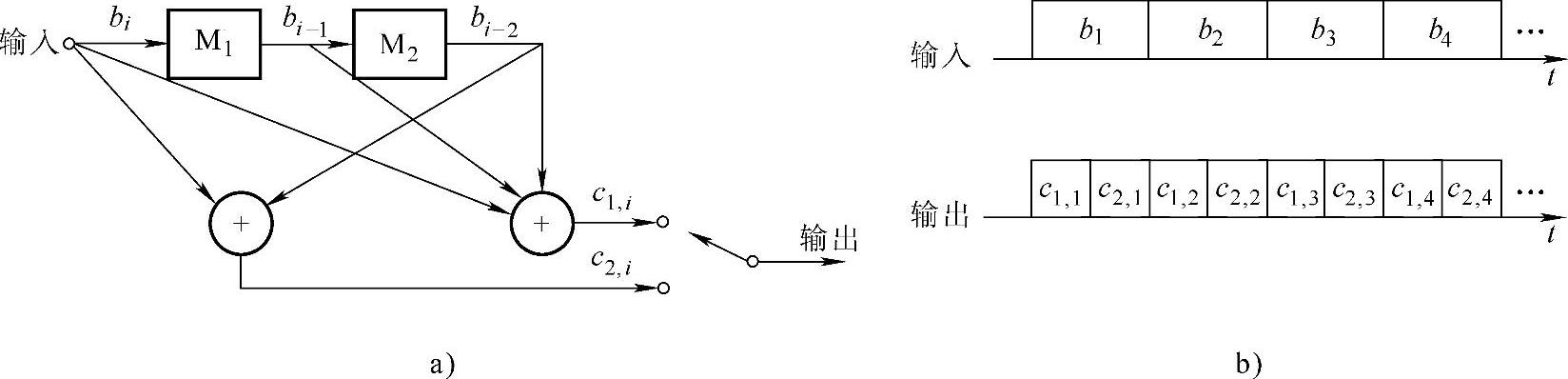
图1-47 （2，1，3）卷积编码器的结构

a）编码器结构 b）输入、输出时序关系

b_i代表当前输入信息位，移位寄存器状态b_i-1、b_i-2存储以前的信息位。上式表明输出是输入的卷积，编码器的输入、输出时序关系见图1-47b。

卷积码常常采用树状图、网格图和状态图进行研究。（2，1，3）卷积码编码电路的树状图如图1-48所示。这里用a，b，c和d表示寄存器M₂，M₁的4种可能状态：00，01，10和11，它们作为树状图中每条支路的节点。以全零状态a为起点，当第1位信息b₁=0时，输出码元c₁c₂=00，寄存器保持状态a不变，对应图中从起点出发的上支路；当b₁=1时，输出码元c₁c₂=11，寄存器则转移到状态b，对应图中的下支路；然后再分别以这两条支路的终节点a和b作为处理下一位输入信息b₂的起点，从而得到4条支路。依此类推，可以得到整个树状图。显然，对于第i位输入信息，图中将会出现2ⁱ条支路。但从第4位信息开始，树状图的上半部和下半部完全相同，这意味着此时的输出码元已和第1位信息无关，由此可以看出把卷积码的约束长度定义为N的意义。图中还用虚线标出了输入信息序列为“1101”时的支路运动轨迹和状态变化路径，从中可以读出对应输出码元序列为“11010100”。

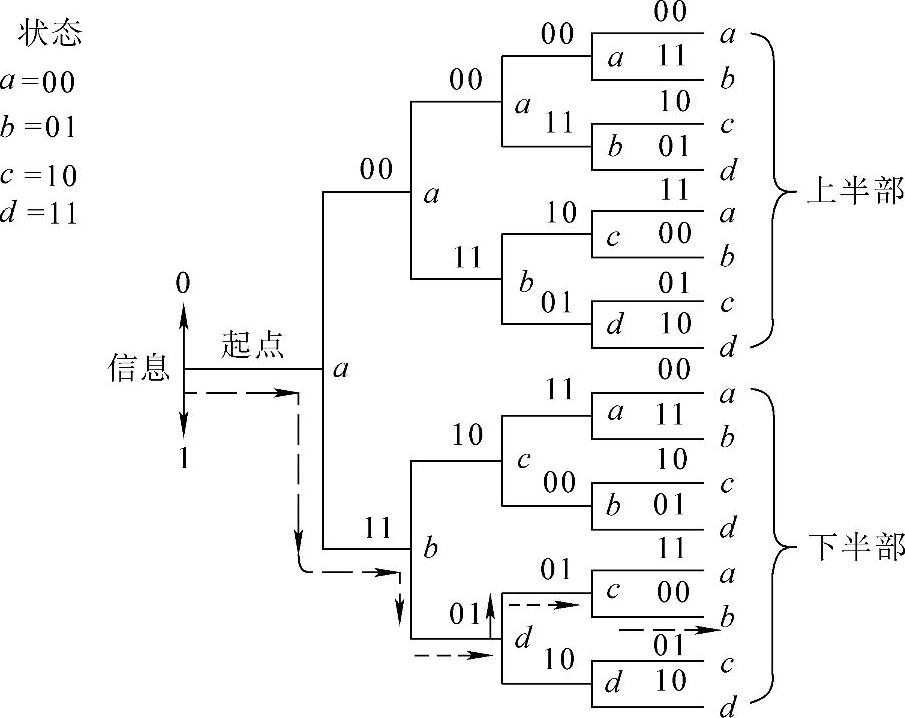
图1-48 （2，1，3）卷积码树状图

利用树状图中观察到的重复性，把其中具有相同状态的节点合并到一起，可以得到更为紧凑的网格图，如图1-49所示。网格图也称格形图，这种图仍由节点和支路组成，4行节点分别表示a，b，c，d4种状态。支路则代表了状态之间的转移关系，其中实线支路代表输入信息为“0”，虚线支路代表输入信息为“1”，支路上标注的码元为当前输出。一般情况下，网格图应有2^k（N-1）种状态，从第N节开始图形同样会出现重复。利用网格图同样可以得到任意输入信息序列下的输出序列和状态变化路径。在图1-48中假设起始状态为0，输入序列为“110111001000”，则对应的输出序列和状态变化将如图1-50所示。

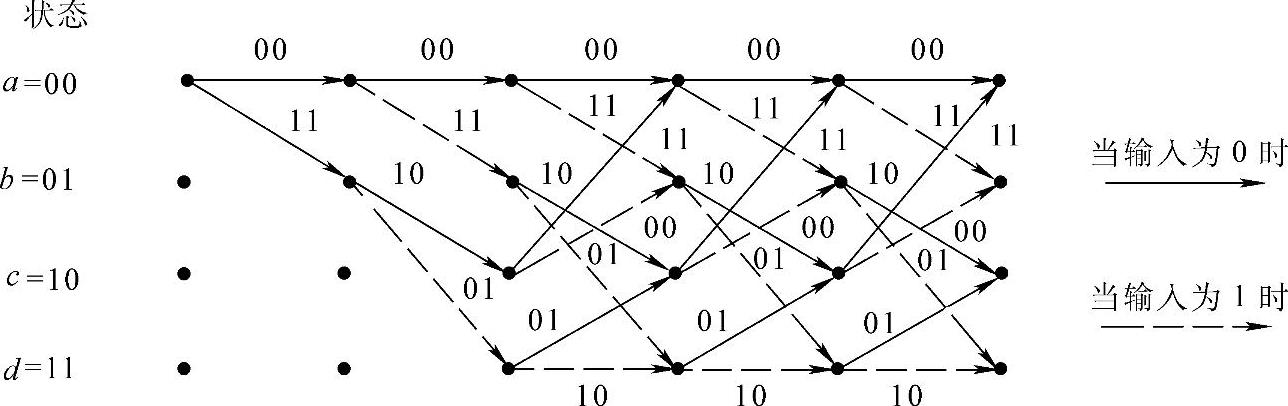
图1-49 （2，1，3）卷积码网格图(www.xing528.com)

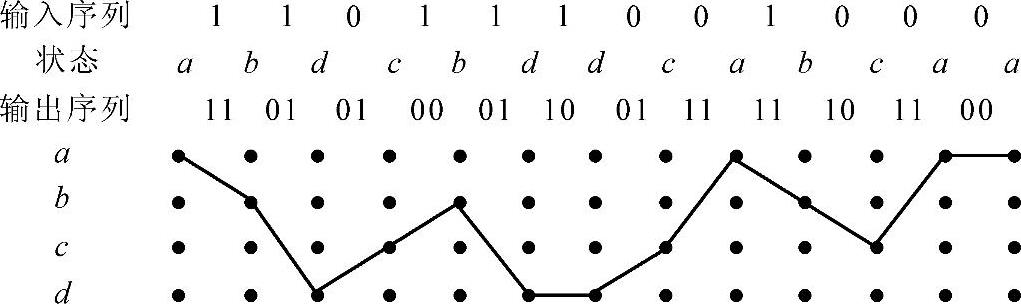
图1-50 （2，1，3）卷积码编码过程和状态变化

图1-51是（2，1，3）卷积码的状态转移图。状态图有2^k（N-1）种可能状态（节点），每个节点会引出2^k条支路，同时也会有2^k条来自其他节点或本节点的支路到达。

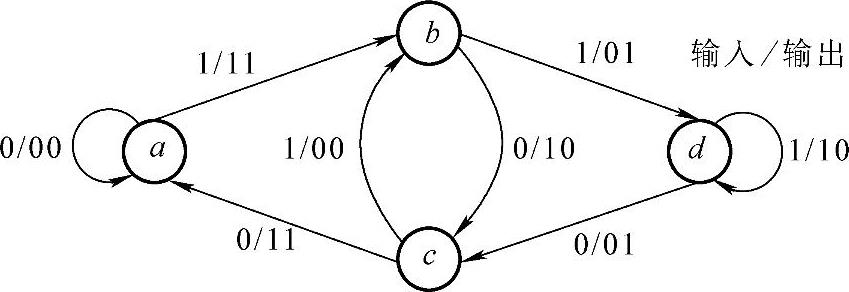
图1-51 （2，1，3）卷积码的状态转移图

注意，在有些资料中把N-1称为卷积码的约束长度，卷积码则记为（n，k，N-1），即本节介绍的（2，1，3）卷积码被称为（2，1，2）卷积码，数字电视中常用的（2，1，7）收缩卷积码被称为（2，1，6）收缩卷积码。本书为了与国家标准GB/T 17700—1999《卫星数字电视广播信道编码和调制标准》中收缩卷积码（2，1，7）的表示一致，把卷积码的约束长度定义为N。

2.维特比译码

卷积码的译码方法分为代数译码和概率译码两大类。前者的硬件实现简单，但性能较差。后者利用了信道的统计特性，译码性能好，但硬件复杂，常用的有维特比（Viterbi）译码。维特比译码比较接收序列与所有可能的发送序列，选择与接收序列汉明距离最小的发送序列作为译码输出。通常把可能的发送序列与接收序列之间的汉明距离称为量度。如果发送序列长度为L，就会有2^L种可能序列，需要计算2^L次量度并对其进行比较，从中选取量度最小的一个序列作为输出。因此，译码过程的计算量将随着L的增加呈指数增长。

维特比译码使用网格图描述卷积码，每个可能的发送序列都与网格图中的一条路径相对应。如果发现某些路径不可能具有最小量度，就放弃这些路径，在剩下的幸存路径中选择。对于（n，k，N）卷积码，网格图中共有2^k（N-1）种状态，每个节点（状态）有2^k条支路引入，也有2^k条支路引出。以全零状态为起点，由前N-1条支路构成的2^k（N-1）条路径互不相交，从第N条支路开始，每条路径都将有2^k条支路延伸到下一级节点，而每个节点也将汇聚来自上一级不同节点的2^k条支路。维特比译码算法的基本步骤为：对于网格图第i级的每个节点，计算到达该节点的所有路径的量度，即在前面i-1级路径量度的基础上累加第i条支路的量度，从中选择量度最小的幸存路径。

DVB-S采用（2，1，7）卷积码，（2，1，7）卷积码有2⁶=64种状态，即S₀～S₆₃，状态号为

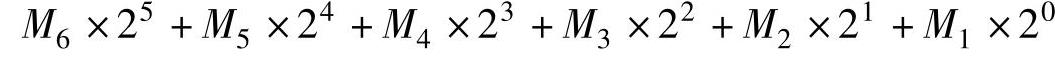
状态转移如表1-5所示。

表1-5 （2，1，7）卷积码编码状态转移表