体积单元算法的应用和优化方法

采用数值算法分析复合材料宏观响应特性，一般选取包含材料微细观特征的局部，即为代表性体积单元。代表性体积单元必须足够大，包含足够多材料细观特征，所反应的材料宏观特性能不因代表性体积单元选择不同而产生差异。从几何尺度上来讲，代表性体积单元尺寸应大于某一临界尺寸，这一临界尺寸即为满足代表性体积单元要求的最小尺寸。而要保证代表性体积单元包含足够多的细观特征，则要求代表性体积单元中所体现的细观特征统计信息与基于更大尺度材料模型统计所得到的规律相一致，因此代表性体积单元的选择尤为重要。代表性体积单元的选择方法主要有四种，分别是胞元方法、周期性微观场法、嵌入胞元方法及窗口方法，其中胞元方法与周期性微观场法应用最为广泛。

胞元方法中多采用单胞模型对材料进行划分，假定颗粒粒径大小相等且规则排列。胞元方法对材料细观结构在一定程度上进行了简化，在提高计算效率的同时，也便于分析某些特定参量对材料宏观特性的影响规律。同时，采用胞元方法分析材料细观特征时，可根据结构特征最大限度地简化模型，并根据对称特性建立二分之一或者四分之一模型。但该方法必须以增强相颗粒或者规则排列纤维，或具有相同的粒度及直径分布为前提，具有一定局限性。

周期性微观场法选取材料中某个局部，考虑材料中增强相尺度、粒度及空间分布等细观特征。以颗粒增强复合材料为例，通过周期性微观场法，可基于统计规律建立包含材料细观结构统计特征的细观仿真模型，也可结合图像处理技术，建立更接近材料真实结构的细观结构真实模型。

基于代表性体积单元对材料进行跨尺度分析时，有限元模型边界条件主要包括混合边界条件、预设位移边界条件和周期性边界条件。研究表明，在不同边界条件下，计算所得材料屈服强度对边界条件较为敏感。具体表现为，施加混合边界条件及预设位移边界条件计算所得材料屈服强度分别偏小与偏大，而周期性边界条件下，计算所得材料屈服强度值准确性最高。

对任意二维代表性体积单元，四个顶点分别为A、B、C、D，模型边界上节点I和J之间满足

式中，α，β=1，2。

对活性毁伤材料力化耦合响应的跨尺度分析基于代表性体积单元有限元模型开展。该模型需满足两个约束条件，一是变形协调，二是应力连续。变形协调指代表性体积单元中相对的面或边的变形是一致的，此为满足其与临近材料点变形场一致的要求。应力连续指代表性体积单元中相对的面或者边的相对节点处应力状态应相同，且应力大小相等。

对代表性体积单元，周期性位移场为(www.xing528.com)

式中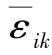，为体积单元平均应变；xk为体积单元内任意点横坐标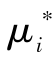；为周期性位移修正量。周期性位移修正量沿不同方向的分量为

式中，“j＋”沿Xj正方向；“j-”沿Xj负方向。

沿Xj正方向和负方向的周期性修正量之差为

对于任意的四边形（正方形、矩形）或者六面体（正方体、长方体），Δ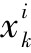为常量，则周期性边界条件的一般性表达式为

式（6.26）中不含周期性位移修正量，在有限元分析中，周期性位移修正量可通过施加多点约束方程的方式来实现。同时正确施加周期性边界条件还需在有限元分析过程中满足边界应力连续条件。研究表明，式（6.26）中给出的周期性位移边界条件能满足相邻代表性体积单元之间的应力连续条件。在代表性体积单元有限元模型分析中，对于任意给定的施加于代表性体积单元变形场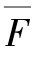，周期性边界条件可用下式进行描述：

式中，Q1为边或面上的节点；Q2为与Q1所在边或者面相对的边或面上对应位置处的点；F为施加在节点上的力；X和x为变形前和变形后物质中的材料点。式（6.27）中前者代表周期性位移，后者为反周期性牵引约束条件。

在有限元仿真中，周期性边界条件的实现方法主要有三种。一是罚函数法，通过引入罚函数，解决数值计算规模与精度方面的问题。二是节点约束法，即根据周期性边界条件约束方程，将对应边上的对应节点进行约束，优点是可以减少约束强度，提高计算结果准确性，实现方法为通过编程识别对应边上的对应节点，针对对应节点的各个自由度，编写约束方程。三是施加载荷法，基于平面假设，对一个面进行法向约束，其他面施加法向耦合使其保持为平面，再对约束面的对立面施加载荷，但缺点是边界条件理想化，易形成过度约束。