冲击引发反应行为的原因分析与探究

冲击引发反应行为主要研究活性毁伤材料在强冲击载荷作用下被激活至反应的响应过程。本节以分离式霍普金森压杆系统为实验手段，分析PTFE/Al活性毁伤材料的冲击引发反应行为。

根据霍普金森压杆理论，加载过程中试样两端应力为

试样中平均应力通过两端应力计算，为

式中，εI，εR，εT分别为入射、反射和透射波在压杆内独立传播时产生的应变；As，AB分别为试样和压杆的截面积；EB为压杆弹性模量。

试样两端应力和试样内平均应力均与压杆弹性模量EB有关，因此压杆材质不同，加载过程中传入试样的载荷不同。研究发现，使用不同材质压杆加载试样，在应变率相同条件下，钢杆加载时试样发生反应，铝杆加载时试样不发生反应。同时，钢杆加载速率必须高于某临界值，试样才会发生反应。因此以钢质和铝质霍普金森压杆系统为例，选择200 mm和300 mm两种长度弹丸，对比研究加载脉宽、加载应力及加载应变率对PTFE/Al反应行为的影响，钢杆和铝杆材料参数如表5.3所示。

表5.3　压杆材料参数

1.加载脉宽影响

针对PTFE/Al（质量分数73.5％/26.5％）活性毁伤材料，分别通过长度为200 mm和300 mm钢弹丸进行加载，试样冲击引发反应过程通过高速摄影记录。加载过程中入射和透射杆施加给试样端面的力分别为

霍普金森压杆加载下PTFE/Al活性毁伤材料试样典型冲击反应过程如图5.26所示。从图中可以看出，试样反应时已被压缩成薄片，因此可认为试样两端受力F1和F2相等，则试样中应力近似为

根据霍普金森压杆测试二波法，试样加载应变率为

式中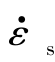，，εR，ls，CB分别为试样应变率、反射波应变信号幅值、试样长度和压杆声速；A为反应时刻残余试样横截面积。

图5.26　PTFE/AI活性毁伤材料试样冲击反应过程

长度为200 mm和300 mm弹丸的加载脉宽分别为80 μs和120 μs，典型加载脉冲波形分别如图5.27和图5.28所示。从图5.27中可以看出，使用长度为200 mm的钢弹丸时，试样在第一个脉冲周期未发生反应，仅变形和破坏；当反射波再次反射加载时，试样发生反应。相比之下，使用长度为300 mm的钢弹丸加载时，试样在第一个脉冲周期发生反应，表明当加载脉冲幅值一致时，载荷脉冲宽度越宽，材料越容易发生反应。

图5.27　长度200 mm钢弹丸典型加载波形

图5.28　长度300 mm钢弹丸典型加载波形

在长度为200 mm和300 mm钢弹丸加载下PTFE/Al活性毁伤材料试样的冲击响应过程如图5.29和图5.30所示。由钢杆材料参数可知，反射波从入射杆/试样界面反射并再回到入射杆/试样界面的时间为475 μs。长度为200 mm的子弹加载时，试样在第一次脉冲周期内未发生反应，因在t=575 μs之前未观察到火光；但当t=600 μs时，反应产生的火光较明亮，故材料反应时刻为575～600 μs，即反应发生在第二次脉冲周期内。长度为300 mm的子弹加载时，在t=100 μs时试样反应即较为剧烈，故材料反应时刻为75～100 μs，即试样在第一次脉冲加载时就发生反应了。

图5.29　在长度为200 mm钢弹丸加载下材料的冲击响应过程

不同长度钢弹丸加载下材料的典型应力-应变曲线如图5.31所示。图中200 mm弹丸加载下的应力-应变曲线由图5.27中第一个脉冲周期得到，曲线总体较短，300 mm弹丸加载下的应力-应变曲线则较长。200 mm弹丸的加载脉宽为80 μs，结合高速摄影，材料在80 μs之前即发生破坏，因此200 mm弹丸加载下，曲线因材料破坏而应力值下降。由此也可确定在300 mm弹丸加载下的应力-应变曲线上材料的失效破坏点。从图中还可看出，300 mm弹丸加载时，试样破坏后的曲线并未下降，而是随应变增大而增加，主要原因是此时加载脉宽较大，材料失效后随即被幅值较大的脉冲继续压缩，材料被压实后，其承载能力并无明显减弱，致使应力-应变曲线并无明显下降。

图5.30　在长度为300 mm钢弹丸加载下材料的冲击响应过程(www.xing528.com)

图5.31　不同长度钢弹丸加载下材料的应力-应变曲线

2.加载应力影响

除了加载脉宽，压杆系统材质直接决定输入材料体系的脉冲幅值，从而显著影响活性毁伤材料反应。为对比加载应力对活性毁伤材料冲击反应的影响，保持弹丸撞击速度为32 m/s，弹丸材料为铝，长度为300 mm，活性毁伤材料试样尺寸为ϕ6 mm×4 mm，与前文在长度为300 mm钢弹丸加载下PTFE/Al活性毁伤材料的冲击反应行为形成对比。

300 mm钢弹丸以32 m/s的速度加载下活性毁伤材料的响应行为如图5.30所示，从图中可以看出，25 μs时，PTFE/Al试样即发生显著破坏和变形；75 μs时，试样压缩变形更严重，快速向外飞散，横截面积明显大于压杆横截面积；在100 μs时，材料剧烈反应，产生黑烟，表明试样在75 μs和100 μs之间发生点火；125 μs时，反应仍剧烈进行，明亮的火焰伴随黑烟向四周扩散，同时可以看出，在两杆界面位置仍有部分未反应材料试样向外飞散。

使用铝杆加载时PTFE/Al活性毁伤材料试样冲击反应典型过程如图5.32所示，试样在60 μs即被压至很薄，发生严重变形，但并未产生显著破碎；80 μs时，试样变形至破碎，且材料沿压杆径向向外飞散，试样横截面积大于压杆横截面积；在100 μs和120 μs时，试样碎裂更加明显，呈粉末状向四周飞散；但是，整个冲击加载过程中未观察到火光，表明试样材料未发生反应。对比以上两种加载方式下试样的响应状态，当加载应变率相同时，钢杆加载下试样发生反应，而铝杆加载下试样未发生反应。这是因为钢杆加载时加载应力约为铝杆的3倍，即加载应力对材料冲击引发反应有显著影响。

图5.32　300 mm铝弹丸加载下材料响应过程

3.加载应变率影响

为对比加载应变率对活性毁伤材料冲击反应的影响，保持加载应力恒定，而加载应变率可通过改变试样厚度实现。实验中选择长度300 mm钢弹丸，速度为32 m/s，试样尺寸分别为ϕ6 mm×10 mm和ϕ6 mm×4 mm。ϕ6 mm×10 mm试样的冲击加载过程如图5.33所示。可以看出，第一个加载脉冲内，试样不断变形，直至100～125 μs，试样横截面开始超出压杆界面，产生部分破坏；但未观察到材料点火产生的火光，表明在第一次脉冲加载内，试样未发生反应。在600 μs时，反射波传回入射杆端，经反射再次加载压杆间残余试样，试样开始粉碎并向四周飞散。直至700 μs时，试样变成粉末，但仍未观察到火光，说明试样在第二次脉冲加载时也未发生反应。

图5.33　Φ 6 mm×10 mm试样的冲击加载过程

对比图5.29和图5.33钢弹丸加载下两种厚度试样的冲击响应过程，可以看出，较薄试样在单次脉冲加载下，快速被压至很薄，最终发生反应；但较厚试样在单次脉冲加载下，仍然保持较大厚度，无明显粉碎、飞散，乃至在后续脉冲加载下仍无法发生反应。两组实验表明，当压杆材质、加载速度和加载应力一致时，加载应变率不同时，试样材料的反应状态显著不同，这说明加载应变率对活性毁伤材料冲击引发反应行为也有较大影响。

以上实验及现象说明了活性毁伤材料在不同加载条件下的典型冲击引发反应特征。基于以上分析，通过保持应力与应变率之一恒定，改变另一参量，可以分别研究加载应力、加载应变率对材料冲击引发的影响，从而确定材料的冲击反应临界阈值条件，研究方案如图5.34所示。

图5.34　应力-应变率阈值研究实验方案

图5.34中L1为等应力线，保持加载应力不变，改变加载应变率（点1至点4）；L2为等应变率线，保持加载应变率不变，改变加载应力（点4至点7）。通过调整加载应力和应变率，即可确定材料发生反应的最低加载应力和应变率。事实上，PTFE/Al这类含能材料的冲击引发往往并非以某个具体的参量值作为阈值，在阈值条件附近反应是概率发生的。因此，按图5.34描述的方案进行实验时，在加载应力和应变率阈值附近会出现既有反应的数据点，也有未反应的数据点的混合区，需要注意混合区数据点的处理方式。

由式（5.18）和式（5.19）可知，加载应力和应变率分别根据该次加载的透射波和反射波计算。加载速度相同时，应变率取决于试样厚度，而对于不同厚度的试样，测试中应力和应变率均呈现近似线性关系。理论上，当实验数据点足够多时，在每条应力-应变率线上均会出现混合区，连接每个混合区的中心点，即可得到划分反应区与未反应区的分界线，即材料是否引发反应的阈值曲线，如图5.35所示，该分界线为代表反应的数据点的包络线，应力阈值线和应变率阈值线为该线的渐近线。在阈值曲线右上方区域内，材料受到的应力和加载应变率均高于阈值，材料会在冲击加载下发生反应。在此区域以外，应力、应变率两者之一或者两者均低于阈值，因此材料不会发生反应。只要实验数据点足够多，通过连接大量混合区中心点，即可大幅提高阈值曲线的预测精度。

图5.35　活性毁伤材料阈值曲线确定方法

1—应变率阈值线；2—混合区；3—阈值曲线；4—应力阈值线

以上分析从不同加载条件下活性毁伤材料冲击引发反应行为的差异角度进行阐述。但需注意的是，活性毁伤材料冲击引发反应行为的另一重要特征是其在反应时的释能效应及其附带产生的超压、温升，而超压、温升效应是活性毁伤元对目标造成结构爆裂毁伤的主要机制。