JCP模型解析与实践应用

对于活性毁伤材料，JCP本构模型也可准确描述其应变效应、应变率效应及温度效应。JCP模型表征了材料流动应力与等效塑性应变、等效应变率及温度之间的关系，一般形式为

图4.38　不同应变率及温度下PTFE/AI材料的应力-应变曲线

表4.15　PTFE/AI材料ZeriIIi-Armstrong本构模型参数

图4.39　ZeriIIi-Armstrong模型预测结果与通过实验得到的应力-应变曲线对比

式中

式中，σ为von Mises等效应力；εp为等效塑性应变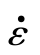；为等效应变率；θ为测试温度；θm为材料熔化温度；A0，A1，B0，B1，N0，N1，θm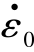，均为JCP模型的参数。从JCP模型的一般表述中可知，温度软化效应、应变硬化效应及应变率强化效应通过相乘的方式解耦，当实际温度θ超过θm时，JCP模型将不再适用。

当塑性应变增加dεp，单位质量塑性功dWp为

忽略弹性功，假设材料密度保持不变，则材料单位质量内能变化为

式中，cV是材料等容比热，假设Taylor-Quinney因子为1，即所有塑性功将转化成热，则在恒应变率、恒定密度、绝热条件下，基于热力学第一定律，由式（4.43）和式（4.44）可得温度与等效塑性应变之间的关系：

由式（4.38）和式（4.45），可得

式中，θi为初始温度，则上式可表述为

式中

PTFE/Al（质量分数73.5％/26.5％）活性毁伤材料在不同温度、不同应变率条件下的应力-应变曲线如图4.40所示。基于JCP本构模型及应力-应变曲线，即可确定PTFE/Al材料JCP本构模型的参数。在单轴压缩测试中，总应变εxx与塑性应变的关系为(www.xing528.com)

图4.40　PTFE/AI材料的准静态及动态应力-应变曲线

式中，σxx为材料的von Mises等效应力，E为弹性模量。通过准静态及动态的应力-应变曲线，可分别获得材料静态及动态弹性模量。结合式（4.50），即可分别获得准静态及动态加载下，材料的等效应力-塑性应变曲线。

在JCP本构模型拟合过程中，假设材料不可压，PTFE/Al（质量分数73.5％/26.5％）材料密度ρ0为2 270 kg/m3，材料等容比热cV为1 161 J/（kg·K）。通过拟合，应变率为0.1 s-1时材料JCP准静态本构模型参数和θm值如表4.16所示，应变率为2 900 s-1时材料JCP动态本构模型参数和θm值如表4.17所示。根据拟合所得本构模型参数，获得材料的等效应力-塑性应变曲线，与不同应变率下实验测试曲线对比，如图4.41所示。

表4.16　应变率为0.1 s-1时PTFE/AI准静态JCP本构模型参数

表4.17　应变率为2 900 s-1时PTFE/AI动态JCP本构模型参数

图4.41　材料JCP本构参数拟合

根据材料准静态及动态JCP本构模型参数，将应变率0.03 s-1作为归一化参考应变率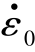，分别代入式（4.39）和式（4.41），即可获得A0、A1、B0、B1、N0和N1等PTFE/Al（质量分数73.5％/26.5％）活性毁伤材料的JCP本构模型参数，如表4.18所示。

表4.18　材料JCP本构模型参数

所得活性毁伤材料JCP本构模型参数的准确性可通过数值仿真与实验对比进行验证。图4.42和图4.43所示为基于JCP本构模型参数对PTFE/Al材料进行泰勒碰撞变形行为仿真与实验结果的对比。从图中可以看出，在104 m/s和222 m/s两种碰撞速度下，仿真结果与实验结果均较好吻合，表明所获得的PTFE/Al活性毁伤材料JCP本构模型参数准确性较高。

图4.42　104 m/s速度时PTFE/AI活性毁伤材料的泰勒碰撞变形

图4.43　222 m/s速度时PTFE/AI活性毁伤材料的泰勒碰撞变形