Zerilli-Armstrong模型：详解及应用

Zerilli-Armstrong模型最早由Zerilli和Armstrong两位学者提出。该模型以位错动力学、晶体结构学和热激活理论为基础，可精确描述材料应变硬化、应变率强化和温度软化效应。不同于经验性的Johnson-Cook本构模型，Zerilli-Armstrong本构模型物理含义清晰，具有显著理论背景优势。

Zerilli-Armstrong本构模型的一般形式为

式中

式中，T为温度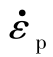；为应变率；p为压力；其余参数均为与材料有关的常数。以上模型中包含13个待定参数，通过实验确定所有参数存在一定的难度，因此在实际应用中，通常假设部分影响较小的参数为0。

假设Bpb=ωp=B0pn=Bpn=B0pb=0，则Zerilli-Armstrong本构模型可被简化为

假设εp=0，T=295 K，则上式可被简化为

令Bpae-β0T=k，则上式变为(www.xing528.com)

此时常数k和β1即可通过对应力、应变率、温度拟合获得。

获得k值之后，β0和Bpa之间的关系为

此时，根据式（4.29），即可拟合获得Bpa取值，确定式（4.34）等式右边的第一项。

式（4.34）右边的第二项表征材料应变硬化效应。当α0=α1=0时，通过应力-应变曲线对下式进行拟合，可得参数ωa，ωb，B0pa值。

PTFE/Al（质量分数73.5％/26.5％）材料在不同应变率及温度下的应力-应变曲线如图4.38所示。拟合获得的Zerilli-Armstrong本构模型参数如表4.15所示，本构模型预测与通过实验得到的应力-应变曲线对比如图4.39所示。