化学反应速率的影响因素

化学反应速率是表征爆炸/爆燃反应体系能量输出结构和做功能力的重要参数。对于活性毁伤材料而言，多组分体系化学反应速率快慢，在很大程度上决定着爆燃超压效应、热效应及其对目标毁伤能力的强弱。

1.化学平衡及平衡常数

化学反应通常发生在多相多组分系统中，使用热力学判据对反应过程的方向和限度进行判定时，需要用偏摩尔量进行相关计算，吉布斯函数的偏摩尔量即为化学势。对于任意化学反应，随着反应进行，各组分摩尔数均发生变化，系统吉布斯函数也随之变化，在恒定T，p，W′=0时，有

式中，μB为化学势。将反应进度dξ=dnB/vB代入式（2.40），得到

式中，（∂G/∂ξ）T，p为一定温度、压力和组成条件下，反应进行了将dξ微量进度折合成每摩尔反应进度时所引起的系统吉布斯函数变化。

换种说法，可以看作无限大量反应系统进行了1 mol进度化学反应时所引起的系统吉布斯函数变化，即摩尔反应吉布斯函数，通常用ΔrGm表示。

根据恒温恒压条件下吉布斯函数判据，有：

若ΔrGm＜0，（∂G/∂ξ）T，p＜0，反应正向进行，反应物自发生成产物；

若ΔrGm＞0，（∂G/∂ξ）T，p＞0，反应不能自发正向进行；

若ΔrGm=0，（∂G/∂ξ）T，p=0，反应达到平衡。

恒温恒压下吉布斯函数值G随反应进度ξ的变化关系如图2.3所示。从图中可以看出，ξ随反应进行而增加；系统吉布斯函数G逐渐降低，降至最低时反应达到平衡。最低点左侧曲线斜率（∂G/∂ξ）T，p＜0，表明反应自发正向进行；最低点处（∂G/∂ξ）T，p=0，系统达到化学平衡；最低点右侧曲线的斜率（∂G/∂ξ）T，p＞0，表明若ξ进一步增加，G将增大，这不可能自发进行。如果系统开始处于最低点右侧，则反应逆向自发进行，逐渐从右侧向最低点趋近，至最低点时达到平衡，即吉布斯函数减小的自发过程。对于恒温、恒容系统，可用亥姆霍兹函数A代替吉布斯函数G进行类似分析。

图2.3　恒温恒压下G随ξ的变化关系

基于平衡条件化学反应方向分析，还可对化学反应平衡进行定量描述，平衡常数Kθ即为最常用的参量之一。平衡常数Kθ热力学定义为

式（2.42）定义表明，平衡常数Kθ除了与热力学函数Δr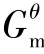相关外，还与反应系统中的平衡组成有关，Δr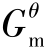可通过三种方法来计算。

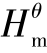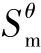①通过化学反应Δr和Δr计算Δr。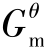

②通过Δf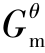计算Δr。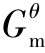

式中，Δf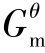为标准摩尔生成吉布斯函数变化，单位为kJ·mol-1。

③通过相关反应计算。

如果一个反应由其他反应线性组合得到，那么该反应的Δr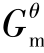可由相应反应的Δr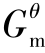线性组合得到。

平衡组成测定必须是反应体系已处于平衡状态，可通过化学或物理方法来测定，如平衡时各组分的浓度、分压等。平衡组成的主要特点：一是在反应条件不变情况下，平衡组成应不随时间变化；二是一定温度下，由正向或逆向反应的平衡组成所算得Kθ应一致；三是改变原料配比所得Kθ应相同。

2.反应速率方程(www.xing528.com)

浓度和温度是影响化学反应速率最重要的因素，化学反应速率方程或反应动力学方程是描述反应速率与浓度、温度、时间之间的关系。在此先分析恒温下反应速率与浓度之间的关系，然后分析温度对反应速率的影响。

对于任意化学反应，定义反应物转化速率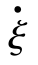为

式中，ξ·为广度量，即单位时间反应进度，单位为mol·s-1。

定义单位体积转化速率为反应速率r，单位为mol·m-3·s-1，即

对于恒容反应，如密闭反应器中反应或液相反应，体积V为常数，即dnB/V=dcB，可用浓度cB代替dnB/V，式（2.46）可写为

对于某指定反应物A或产物Z，通常可用消耗或生成速率来表示。在恒容条件下，反应物A的消耗速率或产物Z的生成速率可表述为

另外，通过反应化学计量式，可以得到反应中某气体组分A的分压与体系总压之间的关系。反应物A基于浓度和分压的反应速率可分别表述为

式中，n为反应级数，对于任一特定反应是个定值；kA为浓度速率常数，单位为mol1-n·m3（n-1）·s-1；kp，A为分压速率常数，单位为Pa1-n·s-1。

对于恒温恒容理想气体A，将pA=cART代入式（2.49），得到

由此可见，在T，V一定时，气相反应速率既可用dcA/dt来表示，也可用dpA/dt来表示，特别是当反应级数n=1时，kA和kp，A相等。

对大多数化学反应而言，反应速率都随温度升高而增大。反应速率随温度变化主要体现为反应速率常数随温度的变化。实验表明，对于均相化学反应来说，反应温度每升高10 K，反应速率常数可增大2～4倍，即

式（2.51）称为范特霍夫规则，k（T）、k（T＋10 K）分别为对应于温度T和T＋10 K时的速率常数，两者比值定性描述了温度对反应速率的影响。

为描述温度对反应速率的影响，阿伦尼乌斯方程（Arrhenius）建立了反应速率常数k与温度T之间的关系，微分形式为

式中，Ea为活化能，单位为J·mol-1，温度变化不大时，可被视为常数。

阿伦尼乌斯方程表明，lnk随T的变化率与活化能Ea成正比。也就是说，活化能越高，反应速率对温度变化越敏感。对于同时存在若干个反应的系统，高温对活化能高的反应有利，低温对活化能低的反应有利。

积分形式的阿伦尼乌斯方程为

式中，A为指前因子，也称为表观频率因子，单位与k相同。

式（2.53）表明，lnk与1/T呈直线关系，如果对一系列（1/T，lnk）实验数据作图，通过直线斜率和截距，可求得相应的活化能Ea及指前因子A。

进一步实验研究表明，当温度变化范围过大时，lnk-1/T图有一定的弯曲，表明指前因子A与温度有关，修正经验关系为

式中，A，B为实验常数，B取值一般在0～4。