热力学状态函数简介

除热力学基本参量外，热力学第二定律描述了热力学过程的方向性，表明了一切自发过程都有方向性，且过程不可逆，常用熵来判断方向性。

1.熵与克劳修斯不等式

卡诺循环是热力学过程分析的基础，即任意一个可逆循环均可分割成无限多个小卡诺循环，每个小卡诺循环的可逆热温商之和均为0，表述为

式中，δQr为小卡诺循环中系统与温度为T热源所交换的可逆热。

式（2.19）表明，对于任意可逆循环，可逆热温商δQr/T沿封闭曲线的环积分为0。也就是说，其积分只取决于系统始态和终态，与过程途径无关。

克劳修斯将上述过程中的状态函数定义为熵（S），表述为

对于非体积功为零的微小可逆过程，由热力学第一定律，有

式（2.21）中右边变量U，p，V，T均为系统的状态函数，其值取决于系统状态，即任何绝热可逆过程熵变均为0，绝热可逆过程为等熵过程。

在熵定义式dS=δQr/T中，温度T总是为正值，对于可逆吸热过程，有δQr＞0，故dS＞0，即系统可逆吸热后熵增加。例如一定量纯物质从固态变为液态再变为气态（s→l→g）的可逆相变过程，整个过程中系统不断吸热，熵不断增加，即Sg＞Sl＞Ss。从系统无序度上看，气态无序度最大，分子可在整个空间自由运动；固体无序度最小，分子只能在平衡位置附近振动；液体无序度介于气态、固态之间。也就是说，系统无序度增加，熵也随之增加。

在微观物理意义上，熵可由统计热力学中玻尔兹曼熵定理给出，即

式中，k为玻尔兹曼常数；Ω为系统总微观状态数。式（2.22）表明，系统总微观状态数Ω越大，系统的混乱度越高，系统的熵也就越大。

卡诺定理指出，工作于T1，T2两个热源间的任意热机i与可逆热机r，可逆热机的效率总是大于或等于任意热机，可表述为

任意热机完成一微小循环后，热温商之和小于或等于零，且等号只在可逆时成立。将任意一个循环用无限多个微小循环代替，式（2.23）可表述为

假设某一不可逆循环，由不可逆途径a和可逆途径b组成。对于不可逆途径a，有

对于可逆途径b，有

式中，下标ir表示不可逆过程；δQr，δQir分别为途径a中由状态1到状态2过程所对应的可逆热和不可逆热。

结合熵定义式，可得到

式（2.27）即为克劳修斯不等式，其中等号只在可逆时成立，表明系统过程的方向可通过比较过程的热温商与熵差（可逆热温商）进行判断。若过程热温商小于熵差，过程不可逆；若过程热温商等于熵差，则过程可逆。

对于单纯发生pVT变化过程的系统，熵变可根据熵定义式，即(www.xing528.com)

对于理想气体或凝聚态物质，若过程绝热（δQ=0），则有

式（2.29）表明，对于绝热过程，熵不可能减小，即熵增原理。一般情况下，系统与环境间往往并不绝热，这时可将系统与环境组成的隔热系统作为一个整体来考虑，该整体显然满足绝热条件，可表述为

式（2.30）即为熵增原理的另一种表述，表明隔离系统熵不可能减小。

不可逆过程可以是自发过程，也可以是依托环境做功的非自发过程。对隔离系统而言，若内部发生不可逆过程，则一定是自发过程，不可逆过程的方向即自发过程的方向。可逆过程属始终处于平衡状态的过程，可表述为

式（2.31）称为熵判据，即通过定量计算系统及环境的熵变，可判断反应过程的方向及限度。系统熵变计算分单纯pVT变化、相变及化学变化三种情况。通常情况下，化学变化过程和反应热都是不可逆的，反应热与反应温度之比并不等于反应熵变。物质标准摩尔熵的确立，使化学熵变计算成为可能。

基于热力学第三定律对熵基准，可以算出某一状态（T，p）下一定量物质的熵，即规定熵或第三定律熵。在温度为T的标准态下，1 mol物质的规定熵即为温度T时的标准摩尔熵，记作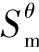（T）。基于标准摩尔熵，即可算得化学变化过程的熵变，判定反应过程的方向及限度。

2.亥姆霍兹函数与吉布斯函数

克劳修斯不等式熵判据应用于隔离系统，需要同时计算系统熵变与环境熵变。在恒温恒容或恒温恒压情况下，利用热力学参量关系可对克劳修斯不等式进行简化，得到更简便的形式，即亥姆霍兹函数和吉布斯函数。

对于恒温恒容且非体积功为零的过程，即δQV=dU，将其代入克劳修斯不等式并进行微分，得到

式中，函数A为亥姆霍兹（Helmholtz）函数。因U，T，S均为状态函数，亥姆霍兹函数A也是状态函数，且为广度量，单位为J或kJ。

将式（2.33）代入式（2.32）中，对于微小过程，可表述为

对于宏观过程，可表述为

式（2.34）和式（2.35）即为亥姆霍兹函数判据，表明在恒温恒容且非体积功为零的条件下，对于一切可能的自发过程，亥姆霍兹函数减小；对于平衡过程，亥姆霍兹函数不变。与熵判据相比，亥姆霍兹函数判据无需考虑环境变化，仅由系统状态函数增量ΔA，即可判定反应过程的方向及限度。

对于恒温恒压且非体积功为零过程，即δQp=dH，将其代入克劳修斯不等式并进行微分，得到

式中，函数G即为吉布斯（Gibbs）函数。吉布斯函数G与亥姆霍兹函数A一样，也是一个广度状态函数，单位为J或kJ。

将式（2.37）代入式（2.36）中，对于微小过程，可表述为

对于宏观过程，可表述为

式（2.38）和式（2.39）即吉布斯函数判据，表明在恒温恒压且非体积功为零的条件下，对于一切可能的自发过程，吉布斯函数减小；对于平衡过程，吉布斯函数不变。吉布斯函数判据应用非常广泛，一是许多相变、化学变化均属恒温恒压且非体积功为零过程，二是也无需考虑环境变化，仅依据系统状态函数增量ΔG，即可对反应过程的方向及限度进行判断。