利用积聚性法求取相贯线表面取点方法

如图3-21小圆柱轴线垂直水平投影面，相贯线的水平投影与小圆柱面投影重合，积聚为一圆；大圆柱轴线垂直侧立投影面，相贯线的侧面投影与大圆柱面投影重合，积聚为一段圆弧，故可利用积聚性的特点，直接求出相贯线的正面投影。

作图步骤：

1）作出相贯线上的特殊点。

因两正交圆柱前后对称，故两圆柱正视转向线正面投影的交点4′、5′就是相贯线正面投影可见与不可见的分界点，4、4″和5、5″为其水平投影和侧面投影的分界点。定出直立圆柱侧视转向线上点Ⅲ和Ⅳ的侧面投影3″、6″及水平投影3、6，由此求出正面投影3′、6′。

2）作出相贯线上的一般点。

在点Ⅳ、Ⅴ与点Ⅲ之间，选两点Ⅰ（1，1′）、Ⅱ（2，2′），求出1′、2′。

根据需要，可再求出相贯线上的足够数量的一般点。

图3-21　求两圆柱相贯线图

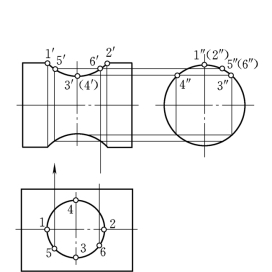
图3-22　求轴类零件钻孔后的相贯线

【例3.9】 如图3-22所示，为一简化后的轴上钻有一圆柱孔，试求出其相贯线。

分析：简化后的轴为一轴线垂直侧立投影面的圆柱，其上的圆柱孔轴线垂直水平投影面，它们的相贯线仍为两轴线正交两圆柱面的表面交线。由于圆柱孔在轴的内部，故其正视转向线的正面投影和侧视转向线的侧面投影为不可见，都画成虚线。正面投影上1′和2′之间无线，因为此处轴的材料已被钻去，钻孔下端画法与上端相同。

讨论：两轴线垂直相交的圆柱，在零件上是最常见的，它们的相贯线一般有如图3-23所示的三种形式。

图3-23　两圆柱相贯线的常见情况

1）图3-23（a）表示两实心圆柱相交，其中铅垂圆柱直径较小，相贯线是上下对称的两条封闭的空间曲线。(www.xing528.com)

2）图3-23（b）表示圆柱孔与实心圆柱相交，相贯线也是上下对称的两条封闭的空间曲线。

3）图3-23（c）表示两圆柱孔相交，相贯线同样是上下对称的两条封闭的空间曲线。

【例3.10】 如图3-24所示，求圆锥与半圆球的相贯线。

分析：圆锥与圆球的三个投影均无积聚性，故相贯线的三面投影均需求出。本例除利用过锥顶的正平面及侧平面作为辅助面外，还须采用一系列水平面作为辅助面来求相贯线。

作图步骤：

1）作出相贯线上的特殊点（转向点）。

图3-24　求圆锥与半圆球的相贯线

过锥顶S作辅助正平面R，它与圆锥面交于两条正视转向线，它与圆球面交于一条正视转向线，两者相交于Ⅰ、Ⅱ两点，即为所求正视转向线上的点。

再过锥顶S作辅助侧平面T，它与圆锥面交于两条侧视转向线，它与圆球面交于一条平行W 面的圆，两者交于Ⅲ、Ⅳ两点，即为所求圆锥侧视转向线上的点。

2）作出相贯线上的一般点。

在点Ⅱ及点Ⅲ、Ⅳ之间适当位置，作一辅助水平面，它与圆锥面交于一水平圆，它与圆球面也交于一水平圆，两者相交于Ⅴ、Ⅵ两点，即为所求。

同理，再作一辅助水平面，又可得相贯线上的两个一般点。根据需要，可求出相贯线上足够数量的一般点。

3）依次光滑地相连各点，并判别可见性。

因相贯体前后对称，故相贯线的正面投影前一半曲线1′—3′—5′—2′与后一半曲线1′—（4′）—（6′）—2′重合，用实线表示。相贯线的水平投影全部可见，画成实线。现在判别相贯线的侧面投影：圆球面和圆锥面的左半部的侧面投影可见，按判别可见性原则可知，属于圆锥面左半部的相贯线可见，即3″—2″—4″可见，画成实线，3″—（1″）—4″不可见，画成虚线。3″、4″为相贯线侧面投影上可见与不可见部分的分界点。圆球面有部分侧视转向线的侧面投影被圆锥面遮挡，也应画成虚线。

4）将两曲面立体看成一个整体，去掉或补上部分外视转向线。如图3-24（b）所示，m处应取掉圆球面正视转向线的正面投影；圆锥面的侧视转向线的侧面投影应画到3″、4″两点。