直线和平面的交点，两个平面的交线

直线和平面的相交只有一个交点，就是直线和平面的共有点。它既属于直线，又属于平面。

两平面的交线是一直线，这条直线为两平面所共有。要确定这一直线，只需确定属于直线上的两点即可。

（1）直线与特殊位置平面相交。

由于特殊位置平面的某些投影（或迹线）有积聚性，交点可直接得出。如图2-54、图2-55所示。

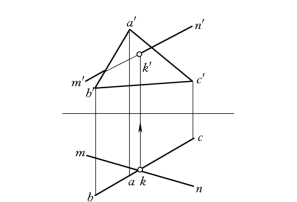
图2-54　直线与特殊位置平面的交点

图2-55　直线与特殊位置平面的交点

图2-54为直线MN 和铅垂面三角形ABC相交。三角形ABC的水平投影abc积聚成一直线。交点K既然是属于平面的点，那么它的水平投影一定属于三角形ABC的水平投影，但交点K又属于直线MN，它的水平投影属于MN 的水平投影。因此，水平投影mn和abc的交点k，便是交点K的水平投影。然后，在m′n′上找出对应于k的正面投影k′。点K（k、k′）即为直线MN 和三角形ABC的交点。(www.xing528.com)

图2-55表示直线MN 和同一个铅垂面相交，但平面以迹线PH 表示。由于PH 有积聚性。故MN 和PH 的交点K 即为所求交点的水平投影。然后，在m′n′上作出对应于k的正面投影k′。K（k、k′）即为所求的交点。

（2）一般位置平面与特殊位置平面相交。

常把求两平面交线的问题看作是求两个共有点的问题。

如图2-56所示，求△DEF 与△ABC的交线。三角形DEF 是铅垂面，直线AC、BC与特殊平面交点的求法在前面已研究过，其作图步骤如图2-56所示，所求得KL即为两平面的交线。

图2-56　一般位置平面与特殊位置平面的交线

图2-57　一般位置平面与特殊位置平面的交线

图2-57表示三角形ABC与同一个铅垂面相交，但铅垂面用迹线PH 表示。PH 有积聚性，其作图步骤如图2-57所示。