【摘要】:图2-50直线∥平面的示意图图2-51判断直线与平面是否平行 试判断已知直线AB是否平行于平面CDE。为此,作属于平面的辅助线FG,先使fg//ab;再作出相应正面投影f′g′,察看f′g′与a′b′是否平行。今f′g′不平行a′b′,则FG不平行于AB,即平面上没有与直线AB相平行的直线。由初等几何知,若属于一平面的相交直线对应平行于属于另一平面的相交两直线,则此两平面平行。图2-53作平面平行于已知平面
(1)直线与平面平行。
由初等几何知道,若一直线平行于属于定平面的一直线,则直线与该平面平行,如图2-50所示。

图2-50 直线∥平面的示意图

图2-51 判断直线与平面是否平行
【例2.6】 试判断已知直线AB是否平行于平面CDE(见图2-51)。
解:问题决定于是否可作出一属于平面且平行于AB的直线。为此,作属于平面的辅助线FG,先使fg//ab;再作出相应正面投影f′g′,察看f′g′与a′b′是否平行。今f′g′不平行a′b′,则FG不平行于AB,即平面上没有与直线AB相平行的直线。因此直线AB不平行于定平面。
(2)两平面平行。(https://www.xing528.com)
由初等几何知,若属于一平面的相交直线对应平行于属于另一平面的相交两直线,则此两平面平行。
如图2-52所示,两对相交直线AB、BC和DE、EF分别属于平面P 和Q,若两对相交直线对应平行,则平面P、Q平行。
【例2.7】 已知实平面由平行两直线AB和CD 决定,试过定点K作一平面平行于已知平面(见图2-53)。
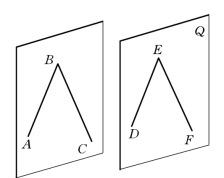
图2-52 平面∥平面的示意图
解:只要过点K作一对相交直线对应地平行于属于已知平面的一对相交直线,所作的这对相交直线便可代表所求的平面。
因此,必须先有一对属于已知平面的相交直线。而题中给了一对平行线,所以,再引属于该平面的一直线MN与它们相交,然后过K引一对相交直线EF和GH,使它们分别平行于直线AB和MN,相交两直线EF和GH确定的平面即为所求。

图2-53 作平面平行于已知平面
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




