换面法：利用新投影面解决几何问题

（1）换面法。

当空间几何元素在两个相互垂直的投影体系中，对某一投影面处于特殊位置时，可以直接利用一些投影特性，解决几何元素的图形和图解问题，从而使作图简单。

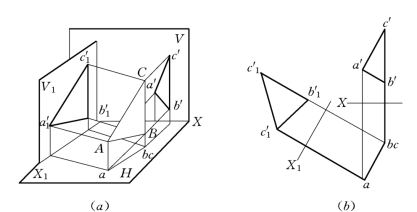
图2-40　V/H 体系变为V1/H 体系

若空间几何元素在两面投影体系中不处于这样的特殊位置时，我们则保留一个投影面，用垂直于被保留的投影面的新投影面代替另一投影面，组成一个新的两面投影体系。使几何元素在新投影体系中对新投影面处于有利解题的特殊位置，以便在新投影体系中作图求解，这种方法称为变换投影面法，简称换面法。

图2-40（a）中有一垂直面三角形ABC。该三角形在V 面和H 面的投影体系（以后简称V/H 体系）中的两个投影都不反映实形。为使新投影反映实形，取平行于三角形且垂直于H 面的V1 面来代替V 面，则新的V1 面和不变的H 面构成一个新的两面体系V1/H。作出三角形在V1/H 体系中的投影。以V1 面和H 面的交线X1 为轴，使V1 面旋转至和H 面重合，求得△ABC在V1/H 体系投影图，如图2-40（b）所示。

由此可见，用换面法解题应遵循下列两条原则：

1）新投影面必须使空间几何元素处于有利于解题的位置。

2）新投影面必须垂直于一个不变的投影面。(www.xing528.com)

（2）点的投影变换规律。

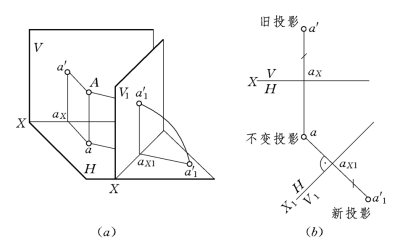
图2-41　点在V1/H 体系中的投影

现在就变换正立投影面时，研究点的投影变换规律。在图2-41（a）中，点A在V/H 体系中，正面投影为a′，水平投影为a。现在令H 面不变，取一铅垂面V1（V1⊥H）来代替正立投影面V，形成新的投影体系V1/H。通过点A向V1 面作垂线，得到新投影面上的投影a′1。这样，点A 在新旧两体系中的投影（a，a′1）和（a，a′）都为已知。其中a′1 为新投影，a′为旧投影，而a为新旧体系中共有的不变投影。它们之间有下列关系：

1）由于这两个体系具有公共的水平面H，因此，A到H 面的距离（即Z坐标），在新旧体系中都是相同的，即a′aX=Aa=a′1aX1。

2）当V1 面绕X1 轴重合到H 面上时，根据点的投影规律可知aa′1 必定垂直于X1轴，这和aa′⊥X轴的性质是一样的。图2-41是点在V1/H 体系中的投影。

根据以上分析，可以得出点的投影变换规律：

1）点的新投影和不变投影的连线必垂于新投影轴。

2）点的新投影到新投影轴的距离等于被更换的旧投影到旧投影轴的距离。