屈曲稳定性的分析方法

屈曲稳定性是结构强度分析中较为特殊的问题。一般地，结构分析通常是根据内力和外力之间存在稳定性的平衡这一假定来求出应力的。这就是说，要达到这样的平衡状态，即：在一定范围内，载荷情况有任何微小的改变时，不会使系统中产生不按比例增加的应力或弹性变形。因此，结构件的安全性的保证依赖于某一定应力（称为许用应力）。而屈曲稳定性问题表现出一个完全不同的性质—要查出外界载荷与结构内部抗力之间可能发生的不稳定平衡。在发生不稳定平衡的瞬间，结构从一种形式的稳定平衡转变为另一种形式的稳定平衡，且伴随着能量的吸收或释放，这个过程中造成了结构件的破坏。例如，研究欧拉杆受轴向压载荷的屈曲稳定性会得到一临界载荷P_cr，当压力P＜P_cr时，杆的直线平衡形式是稳定的；当P＞P_cr时，直线平衡形式变为不稳定的，杆一旦受到干扰便将趋向于弯曲平衡形式。P=P_cr称为平衡的“分支点”，此时的载荷称为临界载荷。屈曲稳定性图例如图12-22所示。

通过基础理论研究和大量实验表明，细长杆、薄壁结构因为其抗弯刚度较低，容易在受压载荷或弯曲载荷状态下发生屈曲失稳。对比此类结构特征，不难看出在风力发电机组中，锥筒式塔筒必须进行屈曲稳定性分析。此外例如，液压变桨机构中的推力杆也应进行屈曲稳定性分析。

目前，应用于风力发电机组中的屈曲稳定性分析方法可分为两类：一类为非线性屈曲稳定性分析，一般流程为

1）在有限元软件中构建结构模型并分网；

2）执行特征值屈曲分析，得到特征值表示的屈曲载荷系数；

3）施加初始几何缺陷或初始扰动，执行非线性屈曲分析，获得临界载荷、屈曲变形以及相对应力分布。(www.xing528.com)

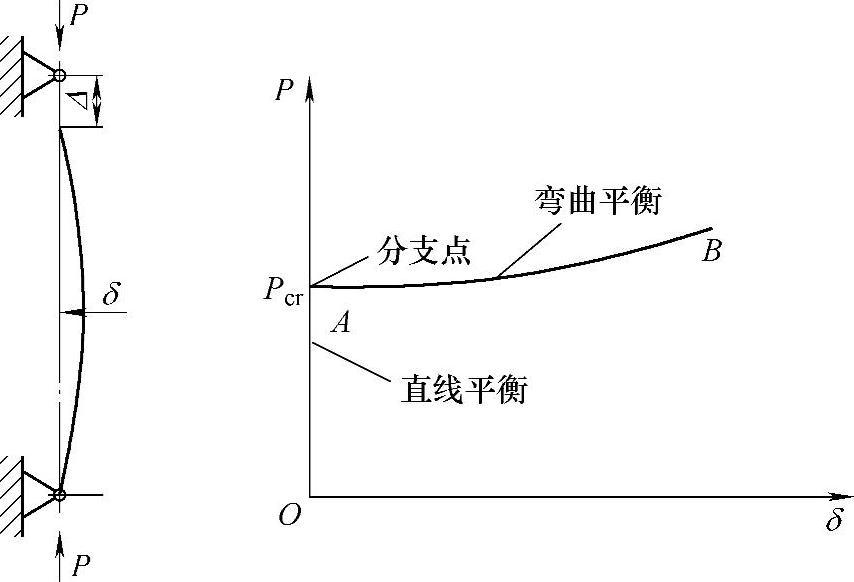
图12-22 Euler杆屈曲稳定性图例

理论上，非线性屈曲稳定性分析可应用于任意复杂的结构件，因算法引入了几何缺陷和载荷扰动，与结构真实的受载状态相似，所以可以得到较好的结果。但是在实际分析中，结果容易受到有限单元质量，初值及非线性算法收敛性的影响，使得结果的可靠程度不高，在计算中应仔细考虑上述影响因素，必要时进行多组对比分析计算。

另一类为工程计算方法，主要针对某些几何特征简单的结构件制定的公式计算法。计算流程可参照相关规范。例如，塔筒屈曲稳定性分析可参照《DIN18800 part 4：Structuralsteelwork Analysis of safety against buckling of shells》。