法兰连接设计及疲劳计算原则

塔架一般由多个法兰段连接而成，每个法兰段又由多个焊接筒节段组成。法兰的实际受力比较复杂，其内力精确计算可根据板块的支承情况采用有限元法进行。在设计中，要求按照GL德国DIN18800 Part 7进行计算，法兰连接的极限计算可采用Petersen方法，而疲劳计算采用Schmidt-Neuper方法。需要强调的是，塔顶法兰由于主机架结构和偏航轴承的影响，工程计算不再准确。塔底同样有门框的应力集中作用，工程计算应予以修正。

对于塔架的环形法兰螺栓连接，GL要求法兰应按照DIN18800 Part 7进行拧紧装配。在法兰的极限状态分析中，螺栓的预紧力可以不考虑，但是局部的塑性化应予以计算。在法兰连接的疲劳分析中，螺栓的疲劳计算应考虑安装预紧力作用。

1.极限强度计算——Petersen方法

Petersen方法只计算最危险螺栓，如图9-19所示。Petersen方法没有考虑螺栓预紧力作用对变形的影响。螺栓只用弹簧模拟，而且预变形为0，其简化模型如图9-20所示。由于弹簧不承受弯矩作用，自然Petersen

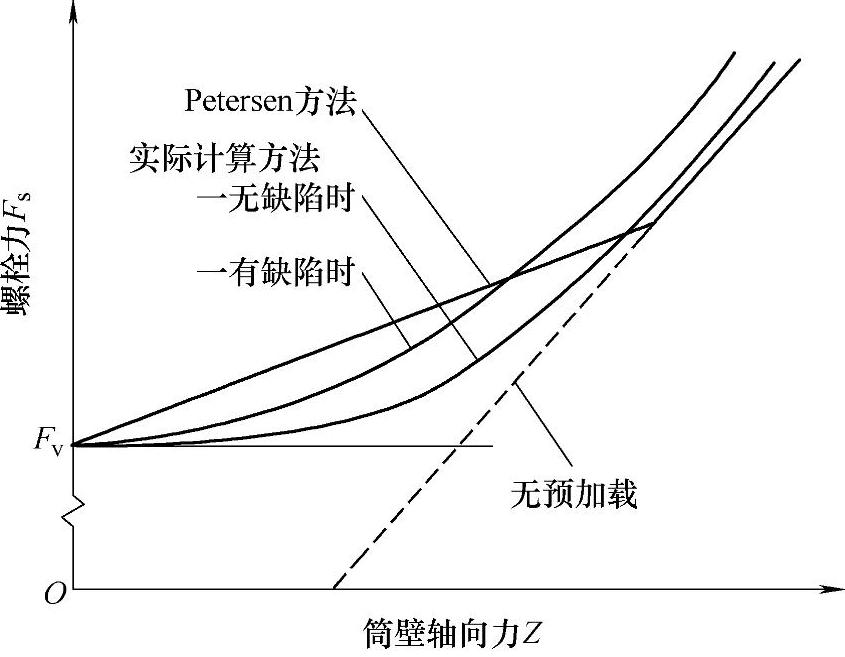
图9-19 Petersen计算方法模型

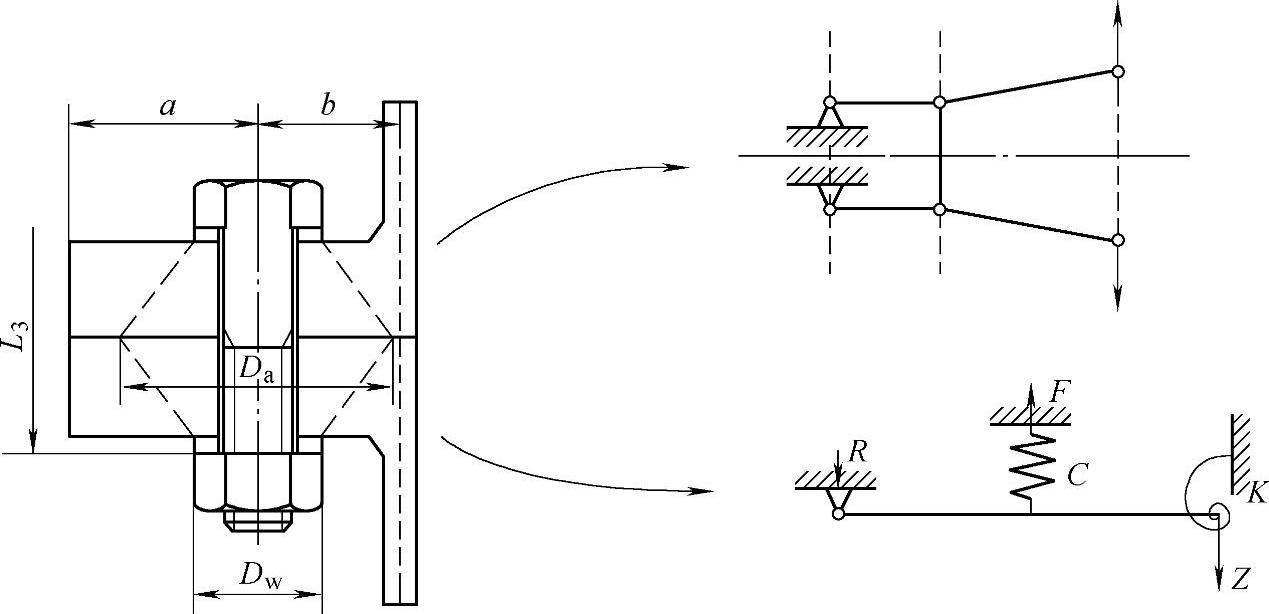
图9-20 Petersen方法的简化模型

方法计算的螺栓没有考虑弯矩的影响，计算模型是不够准确的。但是，Petersen法中对于螺栓采用很大的安全系数，以弥补模型的不足，其计算结果与实验数据基本相符。

（1）弹性设计理论

在Petersen方法中，将法兰假设为梁，采用两条3次曲线模拟法兰的变形挠度曲线，如图9-21所示。

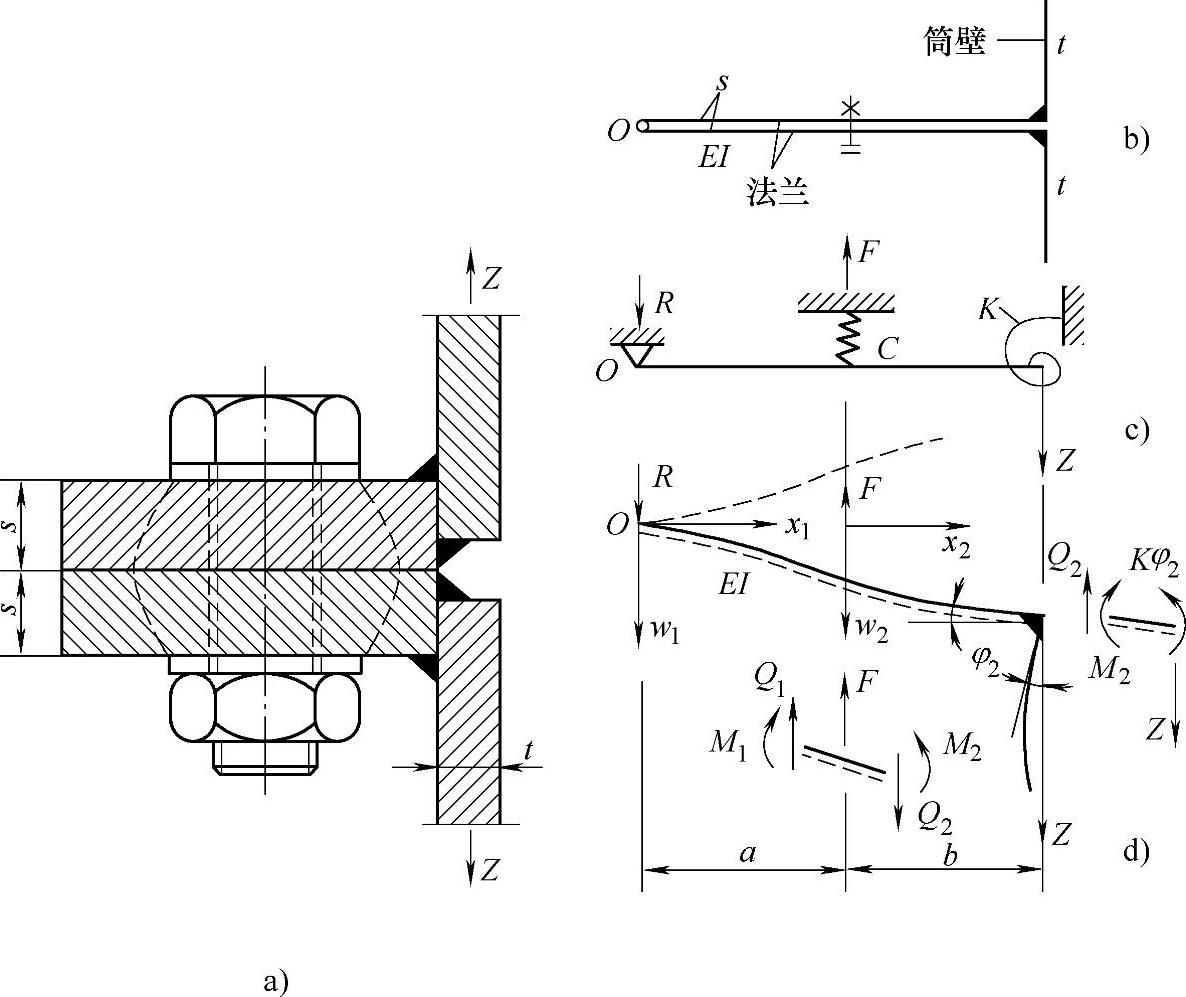
图9-21 法兰的计算模型

其曲线方程如式（9-36）所示。

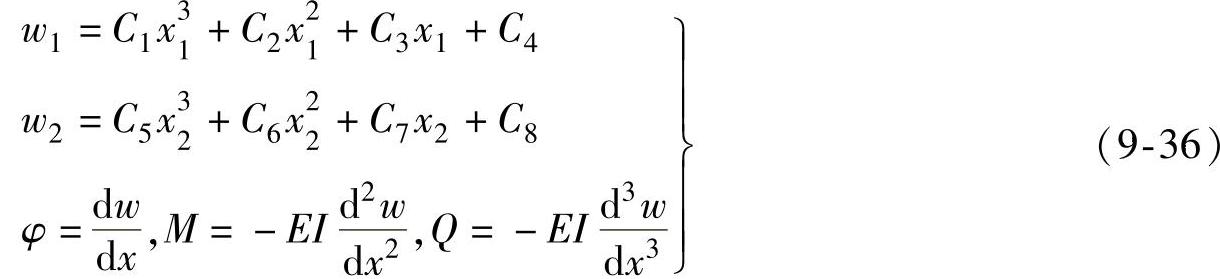
方程中的8个系数由边界条件决定。

1）o点挠度为0，弯矩为0；即x₁=0，w₁=0；x₁=0，M₁=0

2）连接点弯矩平衡，剪力平衡；即x₂=b，M₂-Kφ₂=0；x₂=b，Q₂-Z=0

3）螺栓点处的边界条件有，

挠度相等：x₁=a，x₂=0，w₁=w₂

角度相等：x₁=a，x₂=0，φ₁=φ₂

弯矩平衡：x₁=a，x₂=0，M₁-M₂=0

剪力平衡：x₁=a，x₂=0，Q₁-Q₂+F=0

将8个边界条件代入方程（9-36）中，联立求解曲线系数。

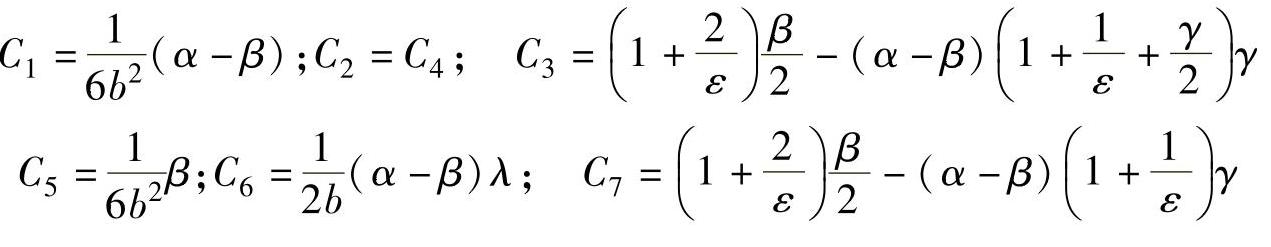
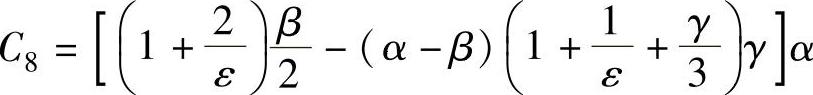
式中 ；；；；；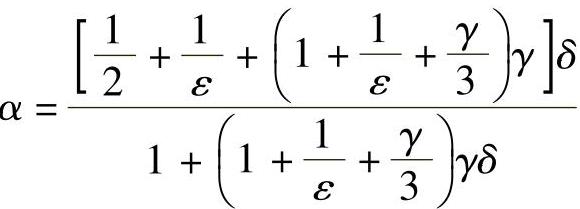

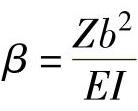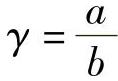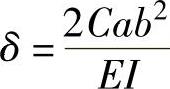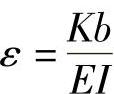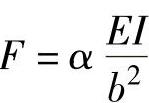
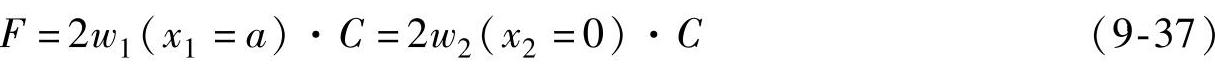
扭转弹簧的弹簧系数K=4EI_s/L_s，如图9-22所示，原始方法主要用于实验对比，对于塔筒结构不能适用。因此，在Petersen方法中特别的将其替换为式（9-38）。

由此，可以通过简化力学模型、法兰几何尺寸a、b、I、c、k等，求得螺栓、法兰内力值，从而进一步验算极限强度。

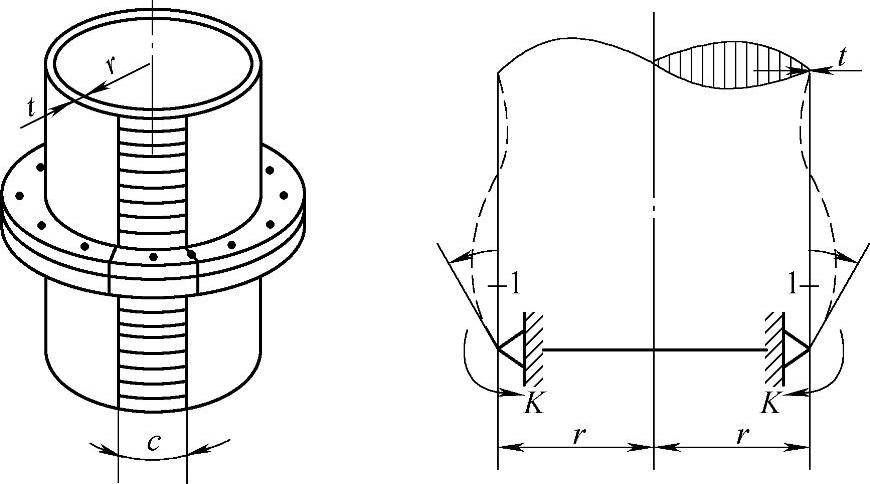
图9-22 弹簧系数

（2）塑性设计理论

上述弹性设计是趋于安全保守的，会造成建造成本的大幅增加。所以，在风力发电机组的设计中法兰连接还可以采用塑性设计原则。

当采用塑性设计时，法兰连接一般有三种破坏方式：螺栓直接拉断；“L”角点发生屈服，螺孔位置与“L”角点同时发生屈服，如图9-23所示。

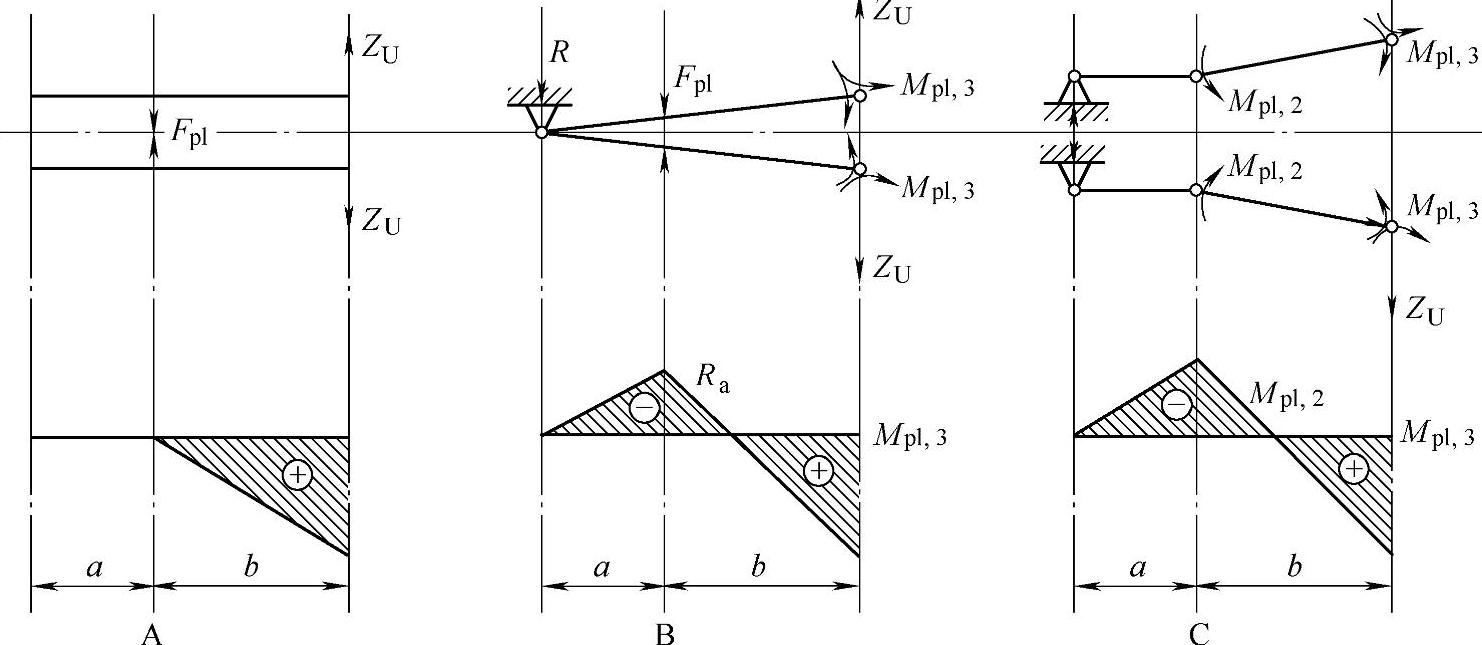
图9-23 法兰的三种破坏形式

可以根据相关截面系数求取截面的塑性承载极限。并根据A、B和C三种破坏方式求取最大承载拉力Z。其中B种破坏方式需要进行收敛计算。

另外，通过等效静力学计算可以得到分度圆弧塔筒上载荷，如式（9-40），与式（9-39）的计算结果基本相同。

（3）计算实例(www.xing528.com)

以图9-24为例具体叙述法兰的计算。螺栓为M16，夹紧长度l_s=4.8cm，a=b=3.0cm，垫片内外径分别为d=1.7cm、D=3.0cm，法兰厚度t=2.0cm，垫片厚度S_s=0.4cm，筒体壁厚s=1.0cm，分度圆弧长为c=16.0cm，假设固定端长L_s=16.0cm，Z=50kN。

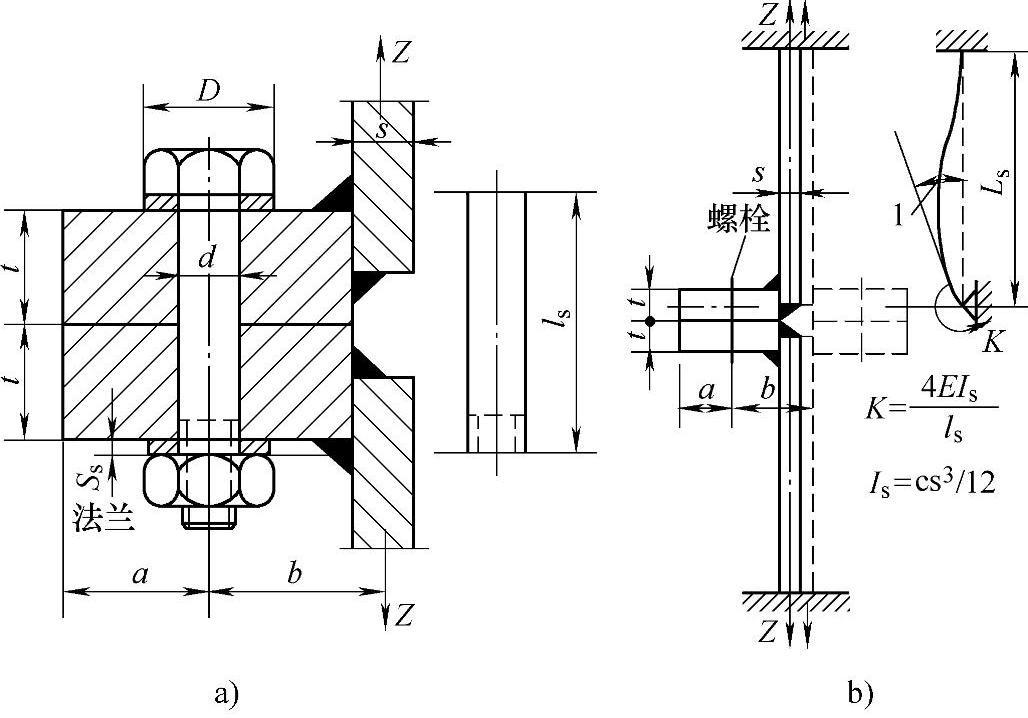
图9-24 法兰计算实例

首先，求解螺栓与法兰的弹簧系数C。

第一步：求解螺栓的弹簧系数C_s。

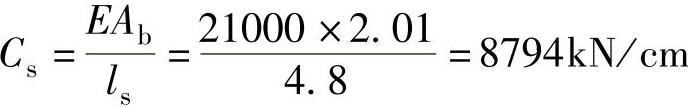
第二步：求解法兰的弹簧系数C_d1和垫片的弹簧系数C_d2。

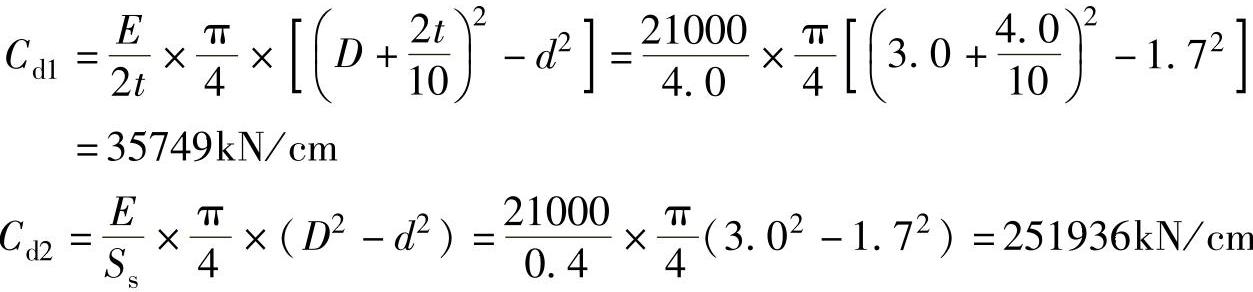
第三步：进行弹簧的串联和并联计算。

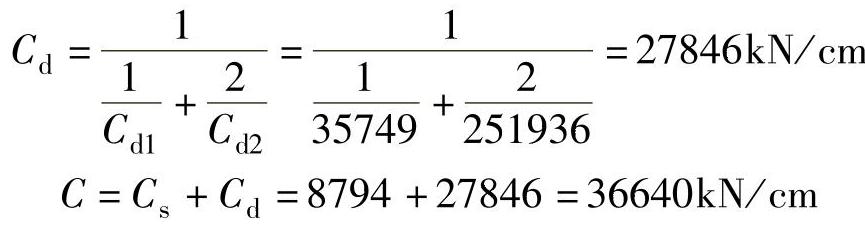
然后，求解扭转弹簧的弹簧系数K。

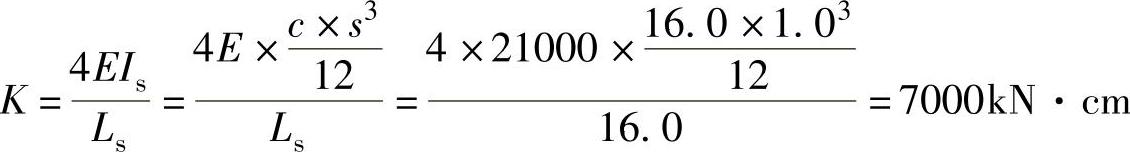
再次，求解截面惯性矩。

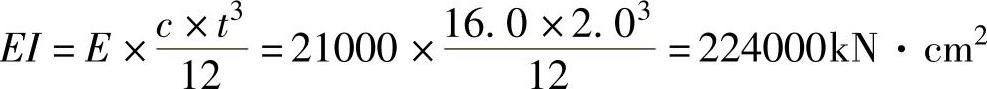
将上述参数代入公式，以法兰连接的几何尺寸参数求解所有的系数。挠度方程也有了明确的数值解。

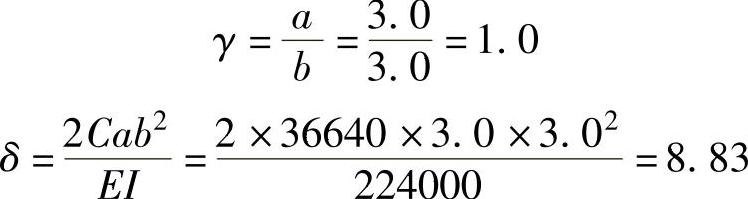
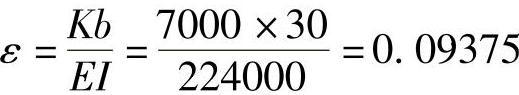：则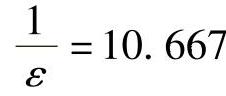

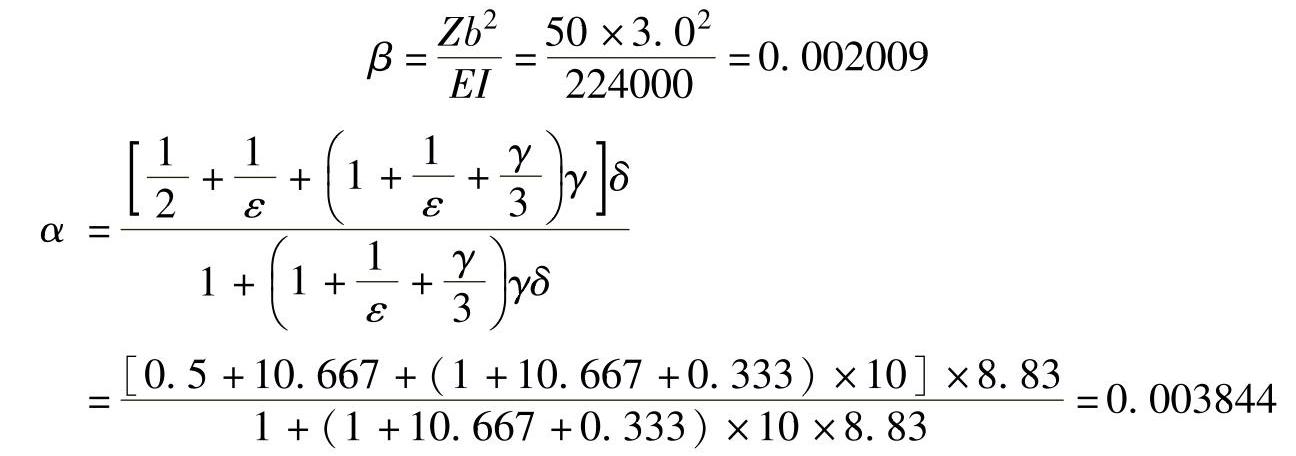
根据弹性理论，求解螺栓的最大拉应力与法兰的最小压应力，要求最大拉应力小于螺栓许用应力，法兰最小压应力应大于0。

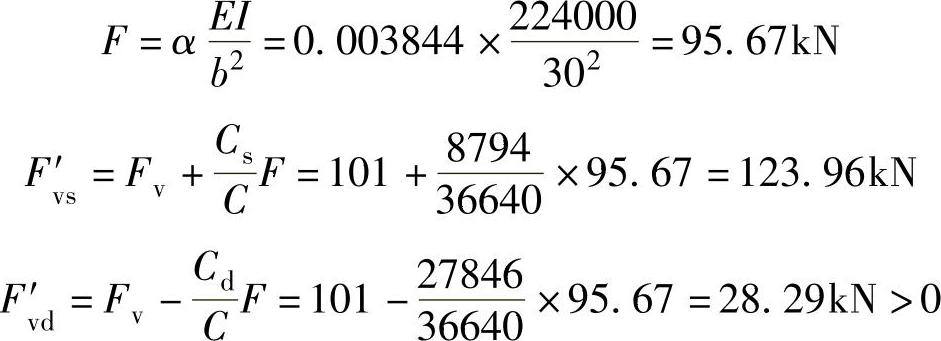
求解螺栓孔位置的最大正应力与“L”形角点的最大正应力，要求两者应小于法兰材料的许用应力。

螺栓孔位置处，x₂=0

“L”形角点处，x₂=b

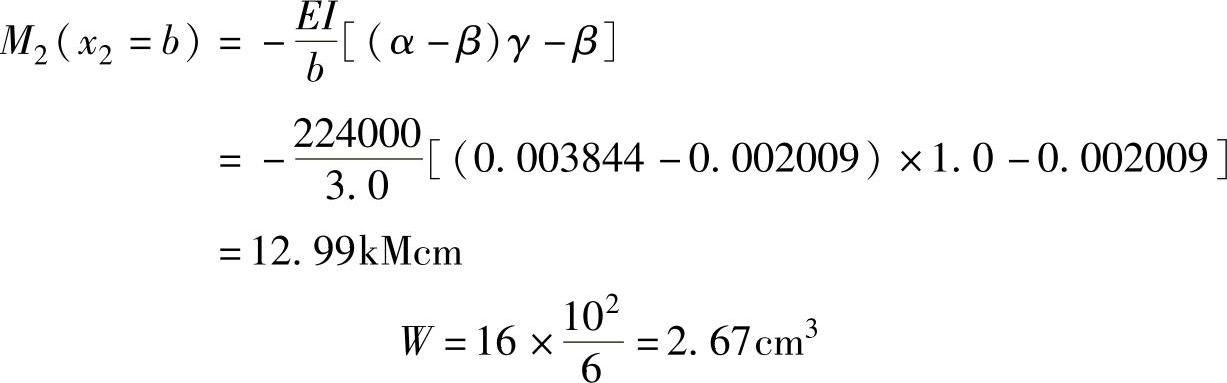
本分圆段筒体的截面积：A=s·L_s=1.0×16.0=16cm²

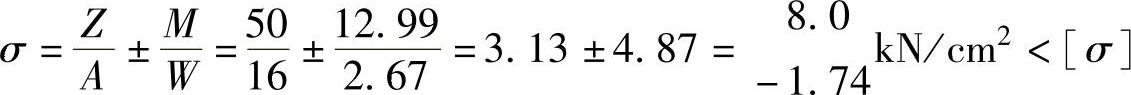
2.螺栓的疲劳计算——Schmidt-Neuper方法

在正常工作状态下，法兰螺栓承受的应力不断变化，由此引发疲劳问题，螺栓的疲劳计算采用Schmidt-Neuper方法，计算简图如图9-25所示。

Schmidt-Neuper方法基于Petersen方法，联合有限元计算分析，并对Petersen方法行了修正。认为螺栓所受载荷F_s与筒壁载荷Z是三段线关系，且与预紧力F_v有很大关系，如图9-26所示。

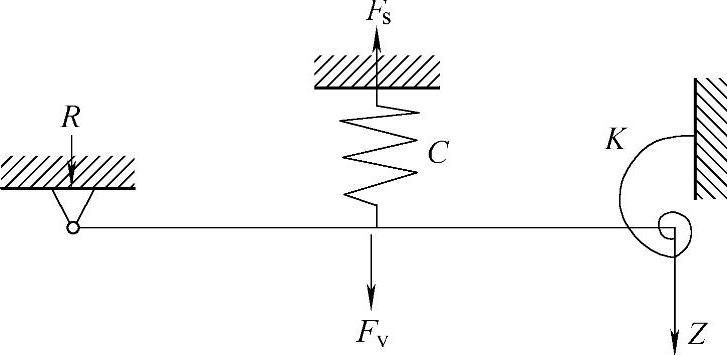
图9-25 螺栓与法兰的简化模型

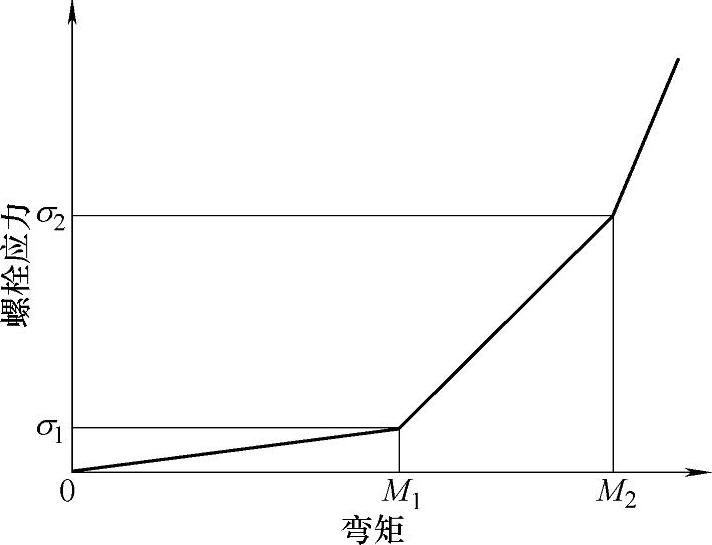
图9-26 Schmidt-Neuper方法的螺栓应力-载荷曲线

当载荷Z一定时，预紧力F_v越小，螺栓受力F_s越大，即斜率越高。即当螺栓预紧力很小时，法兰连接容易开口，导致螺栓承受载荷的比例增大。

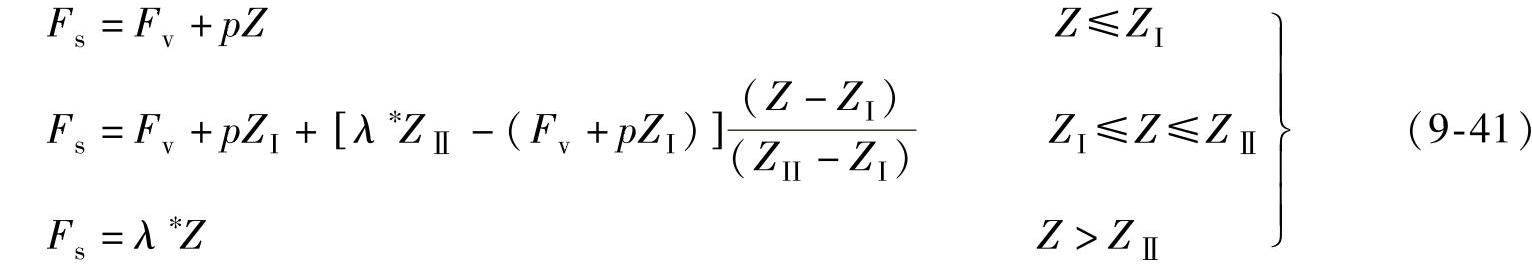
式中 ，，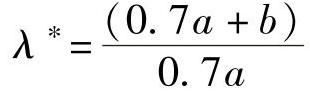

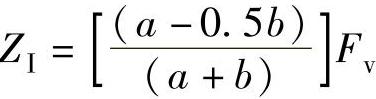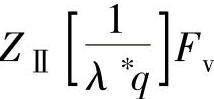
与Petersen方法一样，适用于尺寸（a+b）/t≤3的法兰，且未考虑弯矩对螺栓的影响，因此螺栓要采用一个保守的计算方法。GL规范要求，如果未考虑螺栓所受弯矩影响的话，螺栓疲劳等级应取为36，按照许用疲劳应力验算螺栓的疲劳强度是否满足设计要求。实际设计时，一般采取对S-N曲线进行简化，保证简化后的S-N曲线比GL要求更为保守，如图9-14所示。

3.底法兰连接计算分析

底法兰连接与中间法兰连接计算基本相同，但是要考虑门框对底法兰的应力集中作用，增大法兰的应力。因此载荷Z不能用简单的等效静力学公式（9-39）求解，可以采用有限元计算，获得应力集中系数SCF，代入Petersen方法和Schmidt-Neuper方法进行计算即可。

4.偏航连接强度计算

偏航连接强度计算与变桨距连接强度计算是一致的，两者方法一样。只是主机架刚度对连接螺栓承载情况的影响十分明显，偏航连接强度计算时需要一个完整的主机架（机舱底座）模型参与计算。而轮毂属于厚壁结构，刚度很大，所以计算时可以采用1/3模型进行连接计算。