塔筒屈曲稳定性分析

塔架一般由2～3个法兰段连接而成，每个法兰段又由多个筒节段焊接组成。随着高度、承受载荷的变化，各个焊接段直径和壁厚也会有变化。一般来说，筒体壁厚随高度的增加而减小；但有两种情况例外：

1）在第三法兰段，可能为了保证顶法兰处需要的强度，而增加此焊接段的壁厚；

2）有时也会为了优化风力发电机组的动力学特性或稳定性而改变壁厚分布。塔架作为薄壁结构，需要进行屈曲稳定性分析。

屈曲稳定性分析时，取一个壁厚相同的法兰段作为分析单元，一个法兰相当于一个径向位移约束。计算作用载荷时，可以采用静力等效方法计算，包括弯矩M_xy、压力F_z、剪力F_xy和扭矩M_z等载荷。其受力简图如表9-6所示。

屈曲稳定性的计算方法与塔架焊缝极限强度计算方法一致，区别是破坏准则变为屈曲失稳破坏，许用应力变为许用屈曲应力。其计算过程为：由塔架的理想几何参数计算理想屈曲应力，其次考虑集合缺陷修正为实际屈曲应力，再考虑局部安全系数得到极限屈曲应力。下面以正应力为例予以说明。

1.理想屈曲应力

考虑塔架的锥角影响，正应力计算需要一定的改进。当塔架锥角Q很小时，可以忽略。

当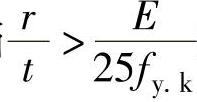时，需要计算筒体屈曲稳定性，其理想屈曲正应力为：

式中 f_y，k——钢材的屈服强度；

σ_xsi——理想屈曲正应力；

l——法兰段长度；

C_x——屈曲稳定系数，按下述方法取值：

当时，为中短筒，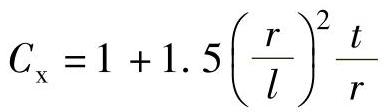

当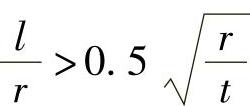时，为长筒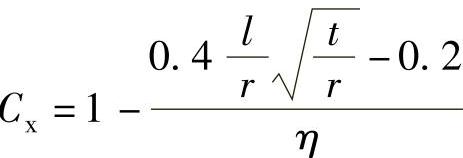，，且C_x≥0.6，η=1。

当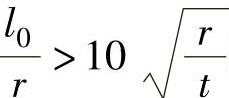时，为超长筒，DIN18800-4不再适用，改用DIN18800-2进行屈曲计算。l₀为计算长度，两端铰支为l，一端固定、一端铰支为0.7l，两端固定为0.5l，一端固定、一端自由为2.0l。

2.实际屈曲应力

考虑实际几何缺陷、结构缺陷、非弹性材料行为，计算实际屈曲应力时，可用下面的修正法。

（1）发生规定范围内的缺陷时的修正

实际缺陷，一般考虑凹陷、圆度和偏心三种：

1）初始凹陷如图9-15所示，规定范围：t_v＜l_mK×1％

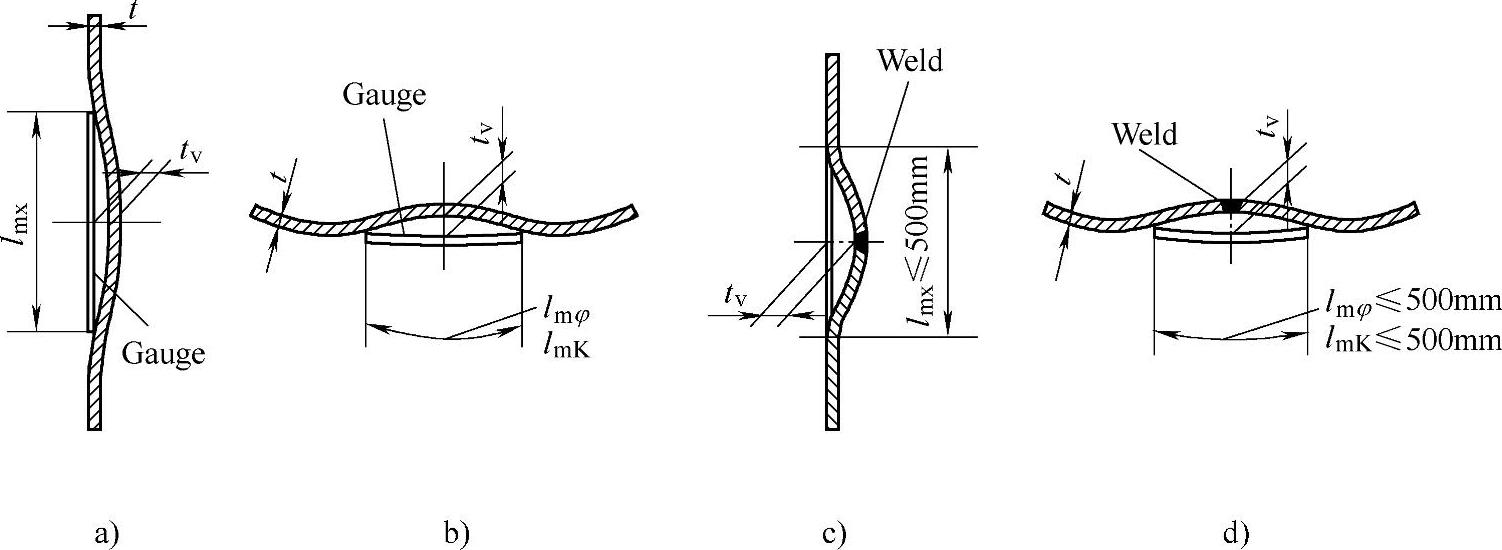
图9-15 初始凹陷示意图

2）圆度如图9-16所示，规定范围：

，

3）偏心量如图9-17所示，规定范围：偏心量e≤0.2t，且不大于3mm

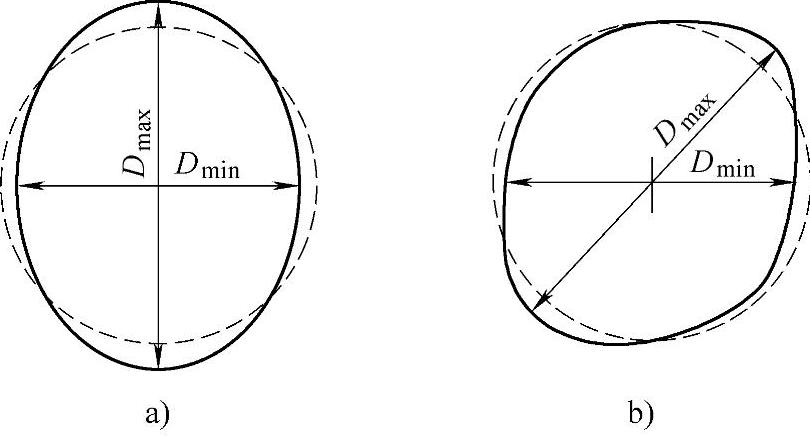
图9-16 圆度缺陷示意图

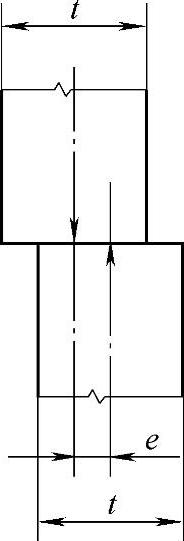
图9-17 偏心缺陷示意图

发生上述范围内的缺陷时，轴向、环向和剪应力分别做如下修正：

轴向应力： σ_xS，R，k=x₂f_y，k （9-24）

式中 σ_xS，R，k——考虑缺陷的实际屈曲正应力；

x₂——实际屈曲正应力修正系数，计算方法如下：

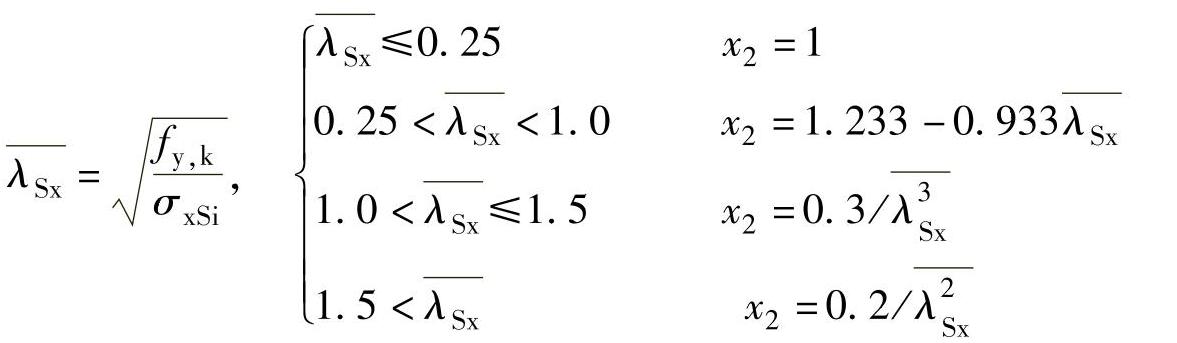
环向应力： σ_φS，R，k=x₁f_y，k （9-25）(www.xing528.com)

式中 σ_φS，R，k——考虑缺陷的实际屈曲环向应力；

σ_xSi——理想屈曲正应力；

x₁——实际屈曲环向应力修正系数，计算方法如下：

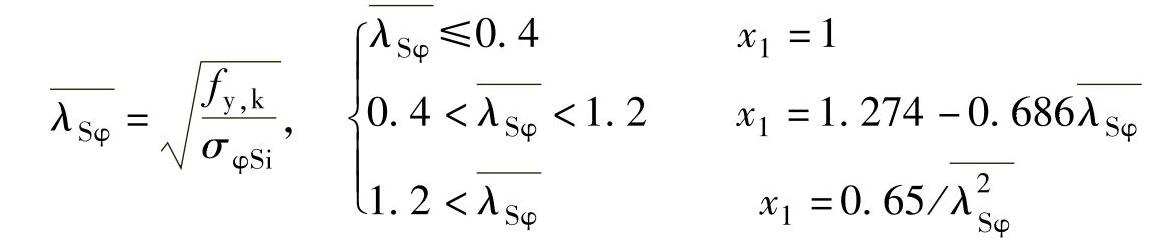
剪应力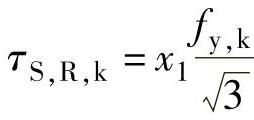： ， (9-26)

式中 τ_S，R，k——考虑缺陷的实际剪应力；

σ_φSi——理想屈曲环向应力；

τ_Si——理想屈曲剪环向应力；

x₁——计算方法如下：

（2）发生超过（1）规定的缺陷时，可采取措施校正缺陷，或采用修正的x值：

当时，

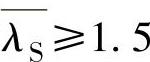当时，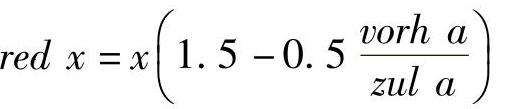

3.许用屈曲应力

考虑局部安全系数，计算许用屈曲应力：

许用轴向应力： σ_xS，R，d=σ_xS，R，k/γ_M （9-27）

许用环向应力： σ_φS，R，d=σ_φS，R，k/γ_M （9-28）

许用剪应力： τ_φ，R，d=τ_S，R，k/γ_M （9-29）

对缺陷敏感性一般的圆度和偏心，实际屈曲应力由x₂获得时，材料安全系数γ_M1=1.1。

对缺陷敏感性高的凹陷，实际屈曲应力由x₁获得时，

需要注意的是，下段塔架门框开口处的许用屈服应力，因为门框开口形状不规则，存在应力集中效应，应力状态比较复杂，因此，计算时应该考虑其影响进行修正。如图9-18中的开口参数符合条件：筒体的径厚比r/t≤160、门洞的张角δ≤60°、门洞的尺寸h₁/b₁≤3时，可用式（9-31）进行修正：

图9-18 下段塔架门框开口示意图

σ′_xS，R，d=C1·σ_xS，R，d （9-31）

式中 C₁=A₁-B₁（r/t），A₁、B₁的取值见表9-7，中间值可用线性内插法计算。

表9-7 参数A₁、B₁的取值

4.屈曲稳定性分析准则

塔架处于不同的载荷工况时，屈曲变形不同，所以对所有的载荷工况都要进行屈曲验算。当单元的实际应力小于许用屈曲应力时，就不会发生屈曲破坏。

对承受单一应力的单元，屈服准则为：

对承受组合应力的单元，屈服准则为