塔架静强度设计及塔筒厚度计算

1.塔筒尺寸的初步设计

（1）塔架的高度

塔架高度的增加可从高空捕获更多风能，降低湍流所造成的影响，并提高年发电量从而为客户创造更多价值。风机的高度每增加一倍，风速增加10％，风能增加33％。相应的，塔架高度增加一倍，为避免塔架的局部屈曲，则塔筒直径和壁厚也要倍增，塔架总重则至少增加到四倍。

因此，塔架高度的选择首先需要考虑风力发电机的规格、风场的风速、安装的具体地理位置和地貌，同时要结合塔架载荷、寿命和制造成本等因素，综合考虑后选定塔架高度。塔架高度一般为叶轮直径的1～1.5倍，如图9-11所示。

综合考虑风力发电机组运作的要求、风场因素、塔架性能及经济方面的因素，塔架的最小高度为

对1MW以下塔架H=h+C+R

对1MW以上塔架H=（1～1.3）D （9-2）

式中 h——为接近风力发电机组的障碍物的高度；

C——为障碍物最高点到风轮扫掠面最低点的距离，一般最小取值1.5m到2.0m；对于MW级机组，叶尖离地距离（h+C）不得低于25m。

R、D——为风轮的半径与直径。

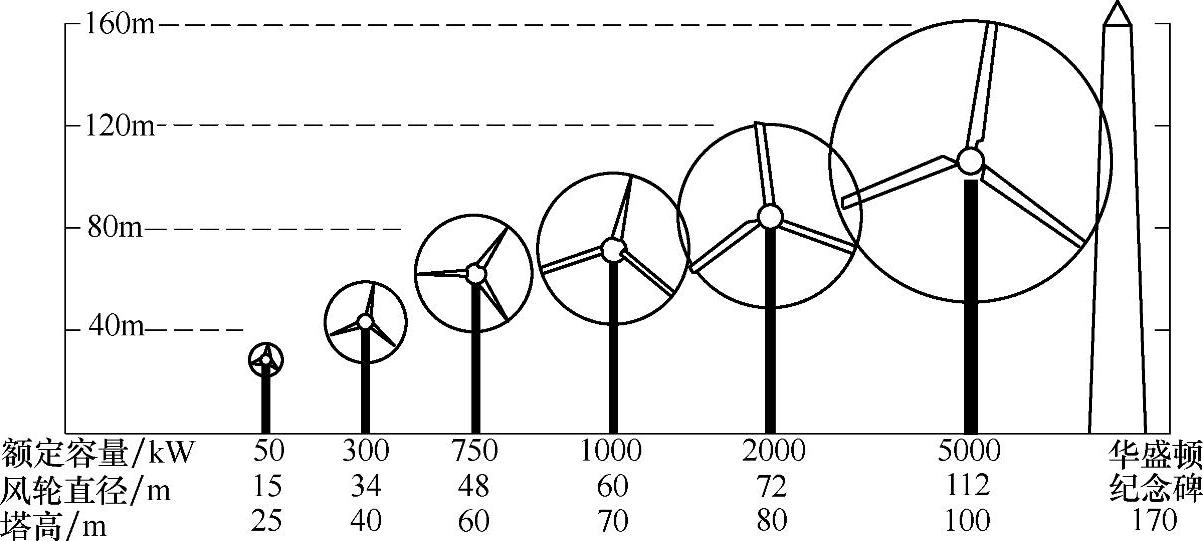
图9-11 塔架高度与风力发电机组功率

（2）塔架的直径

在已有的塔架设计中，根据1MW、1.5MW、2MW和3.0MW塔架的直径与高度的关系分析，高度H与底部直径D之比处于14.8～19.03范围内，见表9-5。

表9-5 高度与直径关系

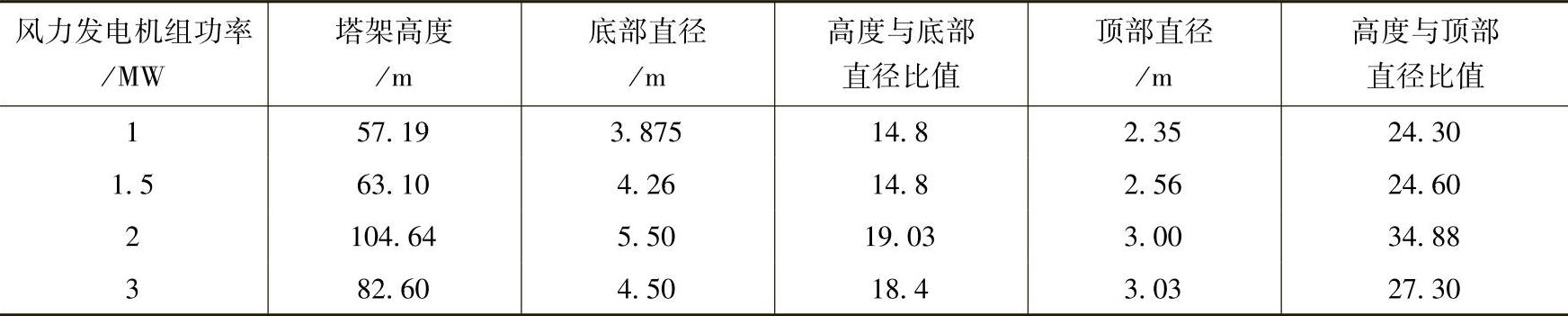
在高耸结构中，如烟囱设计时采用的底部直径D与高度H之比的关系D≥H/20^[10]。通过规范和实际工程实例分析，建议塔架的高度H与底部直径D之比为14～20范围内为宜，当不满足此条件时，塔架底部直径宜扩大。

对于塔架上部直径的确定，主要根据机舱所给定的底部直径来确定。根据以往的经验，高度H与顶部部直径D之比在24～34的范围内。

2.塔架的载荷

塔架的载荷要求在塔架的初步尺寸确定后进行计算。风力机塔架设计载荷包括惯性力和重力、气动载荷、运行载荷和其他载荷（如波动载荷、尾流载荷、冲击载荷、冰载荷等），其设计载荷计算按本书第四章确定，载荷和材料安全系数参见第三章相关内容。

3.塔架静强度计算

塔架静强度计算时，应首先确定危险截面及其截面力。塔架的危险截面一般在塔架的根部。在确定危险截面力时，一般按照刚体假设进行计算。塔架的截面力的计算还应考虑动载荷的影响。

塔架静强度设计时可采用悬臂梁的力学模型。假设受力在材料的弹性范围内，不考虑塔架的塑性变形。对于塔架设计来说首要满足塔架在静力情况下的强度验算，包括正应力、剪应力和扭转应力。

（1）正应力的计算

对于圆锥形塔架，从受到的载荷可以分析得到其应力分布规律是从塔顶到塔底应力逐渐增大，所以塔架最危险截面在塔架的根部。塔架根部的应力公式：

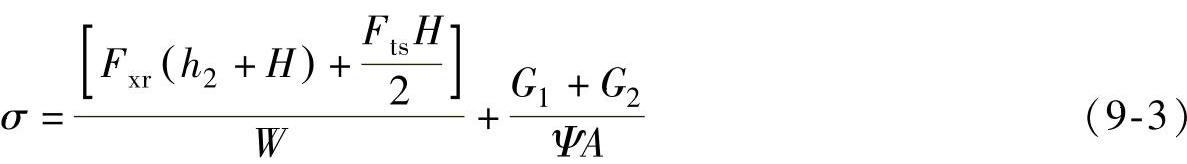
式中 W——塔架根部抗弯截面模量，单位为m³；

F_xr——风轮所受气动推力，单位为N；

F_ts——塔架所受风力，单位为N；

h₂——叶轮中心到塔架上部的距离，单位为m；

H——塔架的高度，单位为m；

A——塔架根部截面积，单位为m²；

G₁——塔架上方所受总重力，单位为N；

G₂——塔架自身所受重力，单位为N；

Ψ——锥形塔架的长度折减系数。

（2）扭应力的计算

工程中发现扭矩对于塔架顶部的强度和风力发电机组的运转影响很大，当塔架顶部的抗扭强度不足时，将会产生塔架的扭转角度过大而影响风力发电机组效率，严重的还会发生扭转破坏。所以，塔架设计时应该进行塔架顶部的抗扭强度和扭转角度的验算，保证塔架的安全。可以将塔架视为壁薄锥筒形式，采用薄壁圆筒扭转的理论方法计算。对于薄壁圆筒，横截面上各点处的切应力可认为与圆周中心处相同，即不沿径向变化，即认为，薄壁圆筒受扭时横截面上的切应力τ₁处处相等，方向则垂直于相应的半径。若塔筒的厚度用t表示，平均半径为r+t/2，则薄壁圆筒横截面上内力的剪应力的大小为

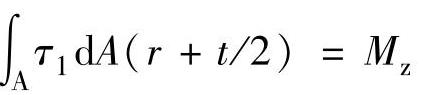
即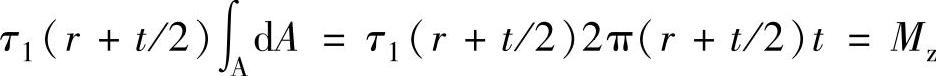

得

式中 τ₁——扭剪应力，单位为N/mm²；

r——圆筒的内半径，单位为mm；

M_z——扭矩，单位为N·mm；

A——圆筒截面面积，单位为mm²；

t——塔筒壁厚，单位为mm。

（3）剪应力的计算

塔架所受的剪力：V=F_xr+F_ts，塔顶处F_ts=0

式中 τ₂——剪应力，单位为N/mm²；

V——剪力，单位为N。

（4）静强度设计

对于塔架的强度验算应分两部分，第一满足抗弯、抗拉压和抗剪扭强度的验算；第二，满足折算应力，通过强度设计可以提出塔架底部及顶部的钢管厚度。

塔架的最大折算应力为

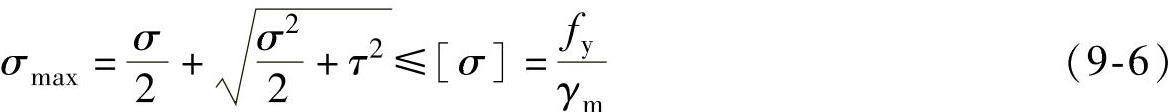
塔架的最大剪应力为

式中 τ——剪应力，单位为N/mm²，τ=τ₁+τ₂；

σ——正应力，单位为N/mm²；

[τ]——许用剪应力，单位为N/mm²，根据材料确定；

[σ]——许用应力，单位为N/mm²，根据材料确定；

f_y——屈服强度，单位为N/mm²，根据材料确定；

f_v——剪切强度，单位为N/mm²，根据材料确定；

γ_m——材料局部安全系数。

将前面初步确定的塔架底部直径和高度以及顶部直径、载荷带入上式中，便可求到塔架筒壁的厚度。

4.塔架的位移和截面倾角以及扭转的验算

对于塔架不仅要进行强度的计算，还要进行塔架的变形验算。如果变形使结构的整体稳定性受到影响，或出现最不利的情况，则计算时应考虑所有因素所引起的变形，包括塔架的弹性变形和由于土壤的柔性引起的倾斜等。塔架在风载作用下会产生变形，这不仅影响了塔架的工作性能，而且由于变形使得风轮与迎风面形成一定的角度，当角度不断增大，风轮与风的有效接触面积就不断地减小，进而影响风力发电机组的效率。所以，控制塔架的变形包括塔顶的水平位移、扭转角度和倾角。

（1）塔顶的水平位移

塔架受到的风载荷简化如图9-12所示。假设塔架变形在材料的弹性范围内，不考虑塔架的塑性变形。通过材料力学可知塔架的在风载的作用下的任意一点的变形。

塔架的弯矩为

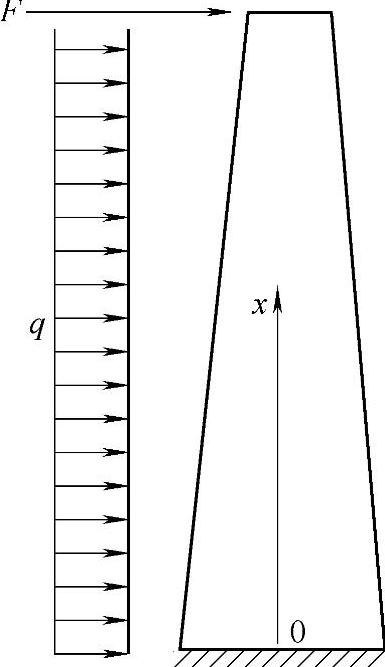
图9-12 塔架的受力简图

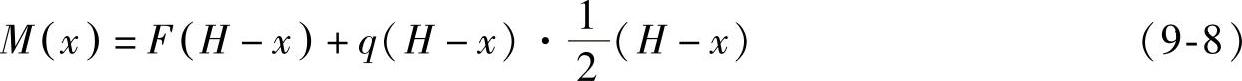
塔架的近似挠度方程试中

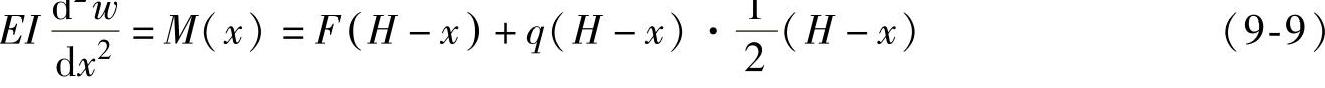
以x为变量进行求解积分得

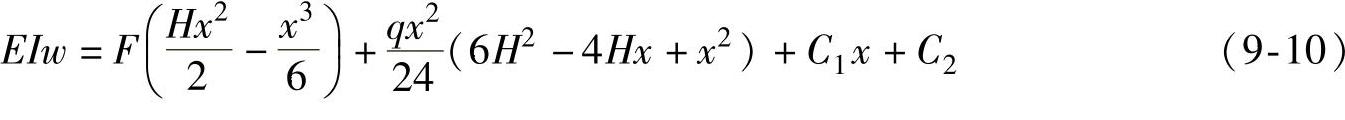
对于塔架的根部处的边界条件为在x=0=处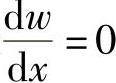，w=0于是得到C₁=0，C₂=0(www.xing528.com)

带入上式得到塔架的挠度

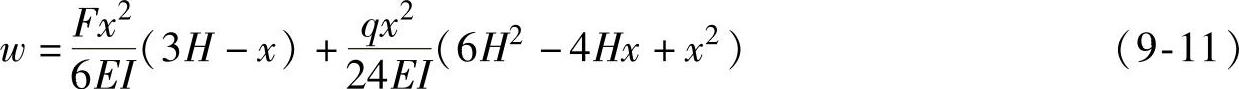
塔架的最大位移出现在塔架的顶部，所以在塔架的变形验算最重要的位置应选择塔架的顶部，将塔架的参数带入上式中整理得到塔架的最大变形如下。

式中 F——风轮及机舱受到的风载荷；

H——塔架的高度；

q——风压；

E——塔架材料的弹性模量；

I——塔架的等效刚度。

对于等效刚度一般采用近似公式：

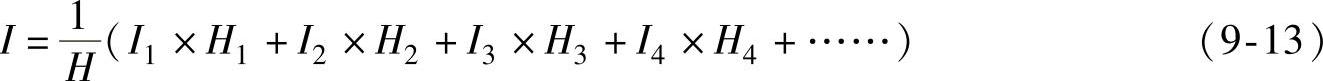
式中 H——塔筒总长；

I₁，I₂，I₃，…，I_n——各区段中点的截面的刚度；

H₁，H₂，H₃，…，H_n——划分的区段长度。

目前，国内的标准和规范尚没有规定塔架许用刚度条件。《高耸结构设计规范》（GB50135—2006）要求结构最大位移的顶点位移不大于总高的1/75，即1.3％H。根据设计和运行经验，确保风力发电机组正常运行的塔架许用挠度[w]一般可控制在（0.5％～0.8％）H的范围内。

（2）倾角

对于塔架来说，当受到风载荷后不但会产生水平的位移，而且还会因为位移造成塔架的横截面与水平方向产生夹角，进而使得风轮与风载荷在水平方向上产生夹角，导致风轮与风的有效接触面积减小，最终影响风力发电机组的效率，所以塔架设计中应该考虑塔架位移产生塔架截面与水平形成夹角造成风轮的有效面积减小，即在设计塔架时，

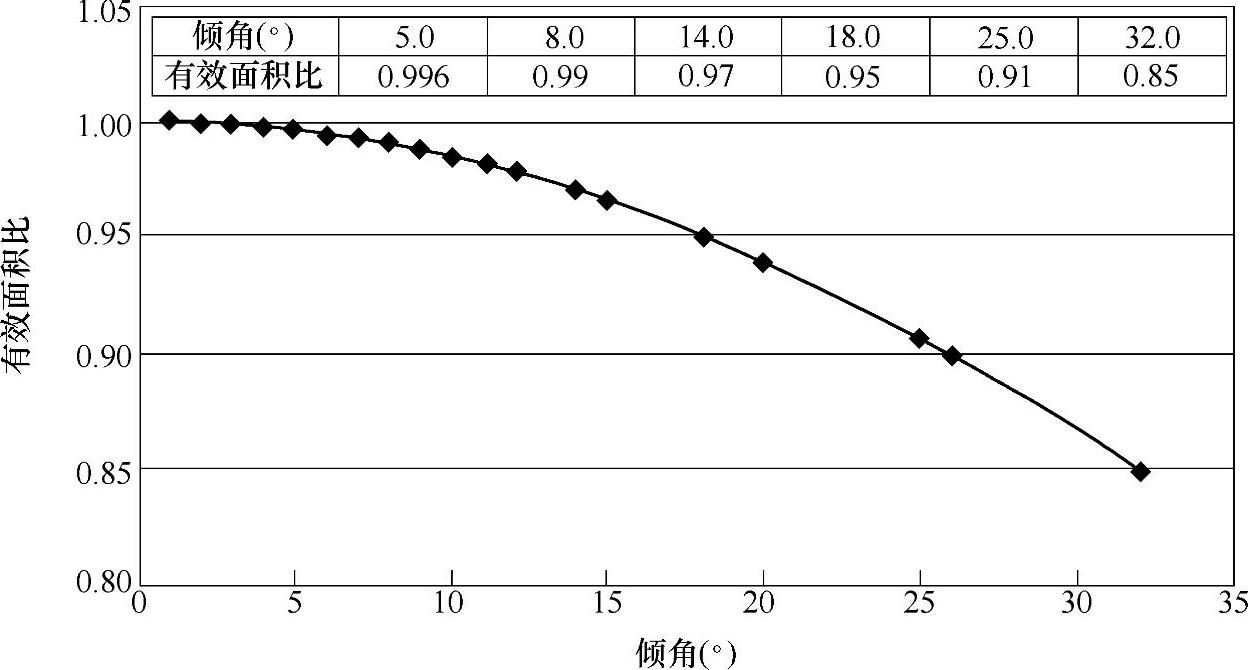
图9-13 塔架倾角与风力发电机组有效面积的关系

控制塔架的横截面与水平方向的夹角。在图9-13中可以看到塔架截面的水平倾角不断增大，风轮的有效接触面积不断地减小，当夹角达到8°时，风轮的有效面积减少到0.99，说明了塔架的倾角对风力发电机组的有效功率的有一定影响，所以在塔架设计时应控制塔架截面与水平倾角。

塔架受到的主要载荷是风载荷，在图9-12中可以看到塔架主要受到的载荷是塔架本身的均布载荷以及塔架顶端受到的风轮和机舱产生的集中载荷，在这两种载荷作用下利用材料力学可知，截面夹角方程是塔架的位移曲线方程的导数关系，对塔架位移曲线进行求导得到下方程：

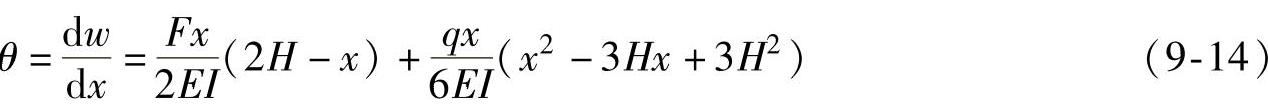
将塔架的参数带入上式中整理得到塔架的最大角度如下：

塔架的许用挠度[w]控制在（0.5％～0.8％）H范围内，进行倾角换算后叶片的倾角范围为（0.24％～0.38％）H弧度。

（3）塔顶的扭转角度

在风力发电机组运行时，需要控制塔架顶部的扭转角度，因此也需要进行计算以保证塔架的安全。

对于扭转角度与扭转应变的关系如下：

即

式中 γ——扭转应变；

φ——扭转角，单位为rad；

H——塔筒长度，单位为m；

r——塔筒内半径，单位为m；

t——塔筒壁厚，单位为m。

参考式（9-4），塔架的扭转角度φ计算公式如下：

式中 G——剪切弹性模量。

5.焊缝极限强度和疲劳强度验算

（1）筒体焊缝验算

塔架的每个法兰段由多个筒节段焊接组成，需要对焊缝的极限强度和疲劳强度进行计算。塔架所受集中载荷位置与焊缝位置的距离较远，内力可以采用静力等效方法进行计算，主要内力一般有弯矩M_xy、压力F_z、剪力F_xy和扭矩M_z，其受力简图见表9-6。

1）极限强度计算：环形焊缝的截面应力可以应用钢结构中的截面应力计算方法。需要分别验算正应力、剪应力和折算应力，如式（9-19）、（9-20）、（9-21）。需要注意的是，当

表9-6 筒体单元的载荷及应力

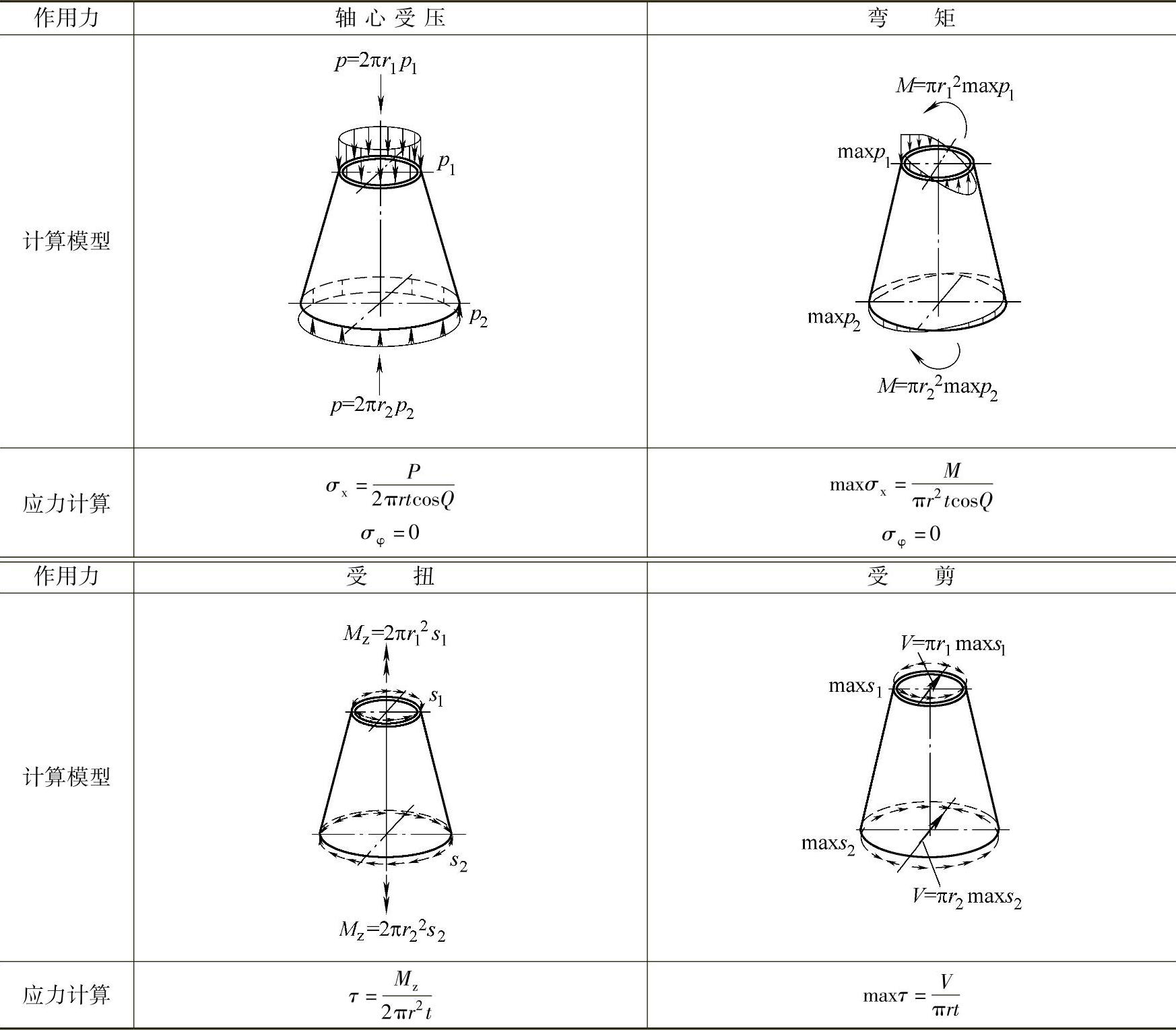
焊缝连接两种不同壁厚的焊接段时，要充分考虑不同截面的应力，需要全部满足强度要求。

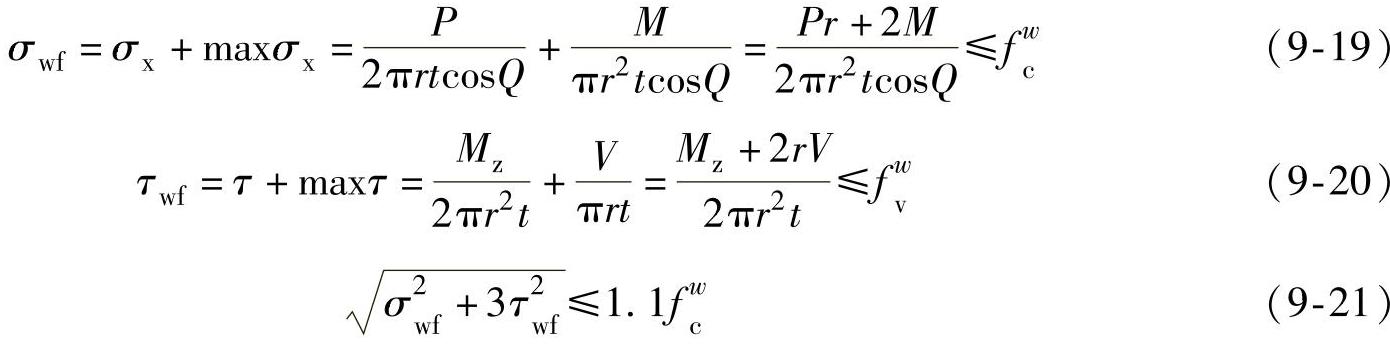
式中 P——轴力，单位为N；

M——弯矩，单位为N·mm；

τ——受扭应力，单位为N/mm²；

maxτ——受剪应力，单位为N/mm²；

τ_wf——焊缝剪应力，单位为N/mm²，根据材料确定；

σ_x——轴力产生的正应力，单位为N/mm²；

maxσ_x——弯矩产生的正应力，单位为N/mm²；

σ_wf——焊缝正应力，单位为N/mm²，根据材料确定；

f^w_c——焊缝受压强度，单位为N/mm²，根据材料确定；

f^w_v——焊缝剪切强度，单位为N/mm²，根据材料确定；

2）疲劳强度验算：对于金属材料的疲劳强度或疲劳寿命的评估采用外加应力S和疲劳寿命N之间关系的曲线叫做S-N曲线，或称为Wohler曲线。对于S-N曲线可分为三部分即低疲劳区、高疲劳区和亚疲劳区。一般高疲劳区和亚疲劳区的S-N曲线按经验方程来取，根据不同的材料、工艺等因素，人们进行了多种多样的疲劳试验，获得了大量的实验数据。根据实验数据，材料的疲劳数据可以绘制出一条S-N曲线，即应力幅值与可循环次数的对数曲线图。当然，每条S-N曲线都有其特定的斜率（m）、疲劳等级（DC）和存活概率（Pu）。

图9-14是对焊缝和法兰螺栓的疲劳强度验算时常用的S-N曲线。为了计算的便捷，在满足德国GL规范要求的那前提下，对S-N曲线进行一定的简化。简化时，要保证简化后的S-N曲线比GL要求更保守，也要求要达到简化计算的目的。

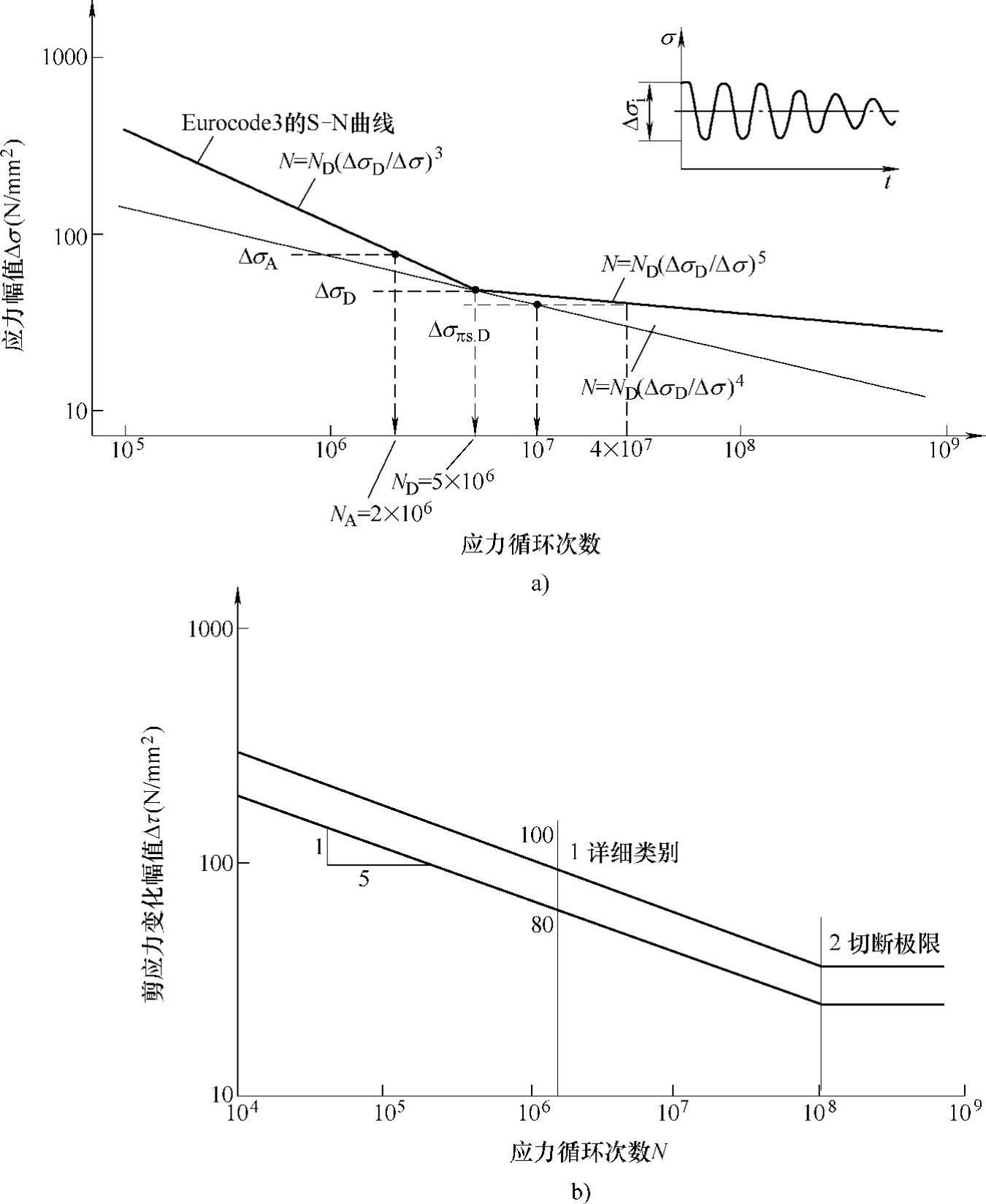
图9-14 焊缝和螺栓正应力和剪应力S-N曲线

a）正应力S-N曲线 b）剪应力S-N曲线

风力发电机组的设计寿命为20年，外载荷对塔架冲击次数约为4.0×10⁷次。因此，焊缝和法兰螺栓的疲劳强度验算时可选重复次数为4.0×10⁷进行验算。这与按修正曲线上重复次数为10⁷的应力范围基本相同。

根据EC31-9的要求，计算焊缝的疲劳时综合考虑焊缝的正应力和切应力，判断焊缝的疲劳损伤：

对焊缝正应力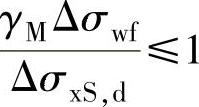

对焊缝切应力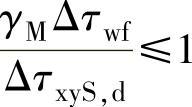

对焊缝综合应力

式中 γ_M——焊缝的材料安全系数，取1.1；

Δσ_xS，d——焊缝的许用疲劳正应力，由焊缝的疲劳等级确定，根据Eurocode 3 part 1，9-Annex B确定焊接等级分别为90，71级；

Δτ_xyS，d——焊缝的许用疲劳切应力，由焊缝的疲劳等级确定。

（2）门框焊缝验算

门框焊缝的形状不规则，存在门洞的缺口效应，其应力状态比较复杂，常用有限元方法进行精确分析。

进行门框焊缝的极限强度分析时，如果没有考虑材料非线性的话，由于应力集中，在焊缝位置不可避免的出现很大的Von Mises应力。当最大Von Mises应力大于许用应力[σ]时，意味着部分钢进入塑性状态。这时，需要满足以下两个条件：

1）超过[σ]区域不能大于壁厚的1/5；

2）这种极端工况必须发生概率极低（如50年一遇）。

进行门框焊缝的疲劳强度分析时，可参考欧洲EC31-9。门框焊缝的疲劳等级为100，工程计算的名义应力不可以继续使用，需要进行焊趾应力计算。焊趾应力外推的计算方法，可以参看国际焊接协会IIW的规定以及EC31-9中的论述。