风轮主轴强度分析及设计参数考虑

1.仅考虑传递扭矩的主轴强度计算

风轮通过主轴将转矩传递给齿轮箱，根据主轴传递的功率要求，首先将功率转化为名义轴向转矩M_xr的表述

式中 M_xr——名义轴向转矩，单位是N·mm；

P——传递的功率，单位是kW；

n——主轴转速，单位是r/min。

该转矩作用在主轴，将产生扭剪应力τ（MPa），为了使主轴能承载给定转矩，应对其进行校核计算。最大扭剪应力应发生在轴外表面，即r=r₀处。强度条件为

式中 W_T——轴抗扭截面模量，单位是mm³，对圆截面轴

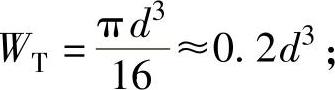
[τ]——轴的许用剪切应力，单位是MPa。

2.主轴直径初步估算

由式（8-2）可得轴径初步估算公式

式中 d——主轴直径，单位是mm。

式（8-3）计算结果可作为主轴上只承受转矩部位（如主轴轴头与齿轮箱连接处）的直径。

实际设计中，上述计算通常应考虑一定的安全系数，对不同的材料，一些机械设计手册给出了推荐最大应力。

【例8-1】 某机组主轴设计，已知风轮吸收的额定功率为3000kW，主轴转速为12.5r/min，所选主轴材料许用剪切应力[τ]=55MPa，试估算主轴直径。

解：该主轴传递的转矩为

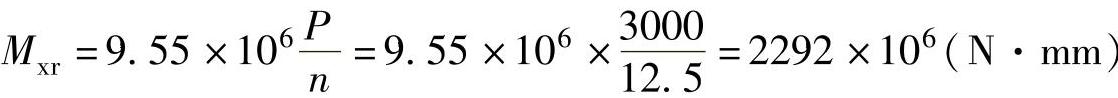
所需主轴最小直径为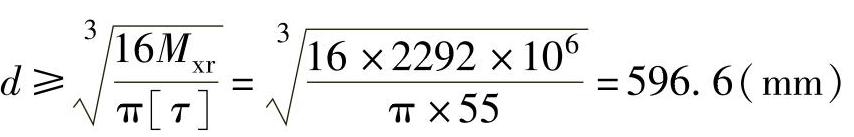

3.考虑综合载荷作用的主轴强度计算

主轴的功用不仅是将转矩传递给齿轮箱，同时还要在轴端支撑巨大的风轮。因此，主轴承受的载荷情况比上述仅承受扭矩作用的情况要复杂得多，通常是在式（8-3）基础上做主轴的结构设计后，再对主轴做精确的强度计算。考虑载荷及主轴上零件的安装情况，主轴结构通常呈轴头处为细端的圆锥形，并且在前主轴承位置承受最大弯矩。在结构允许的条件下，可将主轴尽量设计得保守一些。根据设计实践，考虑全部载荷作用条件下，风轮主轴直径（主轴承处）通常取为风轮直径的1％左右，轴头直径按式（8-3）计算，按此设计参数一般可以保证其强度。

对于一般的轴，在弯扭应力共同作用下，初步设计时，可按第三强度理论计算其强度：

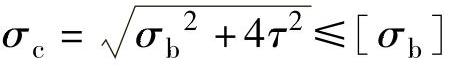
式中 σ_c——合成应力，单位是MPa；

σ_b——危险截面上的弯曲应力，单位是MPa；

τ——扭剪应力，单位是MPa；

[σ_b]——许用弯曲应力，单位是MPa。

按照图8-5所示支撑结构，显然主轴在主轴承处承受最大弯矩M，该处所受合成应力为

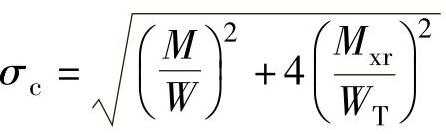
式中 W——抗弯断面模量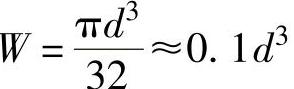，，单位是mm³；

W_T——抗扭断面模量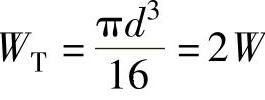，，单位是mm³；

M_xr——工作转矩，单位是N·mm；

M——前主轴承处主轴所承受的弯矩，M=M_K+G_wl₁；

G_w——风轮重力，单位是N；

l₁——风轮重心到轴计算截面距离，单位是mm；

M_K——偏航时风轮的回转力矩，单位是N·mm。

因此，其强度条件为

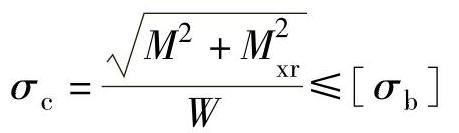
考虑到弯矩M作用下产生的正应力是对称循环应力，而转矩M_xr作用下产生的剪切应力可认为是脉动循环应力，应对上式做以修正

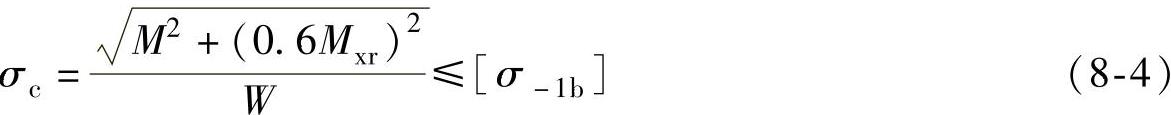
式中 [σ_-1b]——对称循环变应力下的许用弯曲应力，单位是MPa。

4.空心轴的强度计算

通常主轴都做成空心的，以便通过变桨距控制线缆或通过液压变桨距装置。对于空心主轴，式（8-4）可改写为

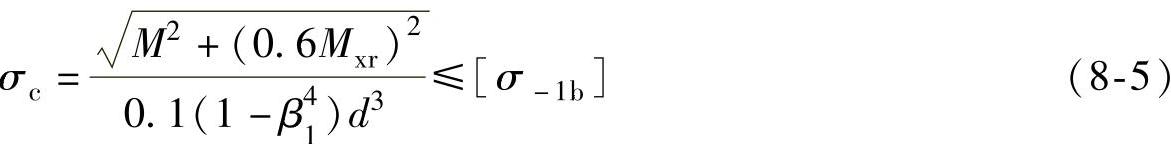
式中 β₁——空心轴内、外径之比，β₁=d₁/d。

5.疲劳强度计算

疲劳强度计算应首先确定在一定的应力幅值S下主轴失效的应力循环次数N，即N-S曲线。

N-S曲线可以由实验室小试样实验得出。但是，由于以下因素的影响，应该对小试样实验得出的N-S曲线进行修正。这些因素是技术尺寸效应、几何尺寸效应、表面质量和应力集中等。

（1）技术尺寸效应

试样通常具有较小的尺寸（直径一般为5～10mm），其力学性能通过锻造或轧制减少了横截面积得到提高。技术尺寸效应可以用技术尺寸系数ε₁来考虑（见图8-6）。在图8-6中，d表示所考虑主轴的直径。

（2）几何尺寸效应

不同尺寸的试样具有不同的疲劳性质，可以使用几何尺寸系数ε₂来考虑（见图8-7），如果纯拉压的疲劳强度可以作为计算的基础，其ε₂可以设定成等于1。(www.xing528.com)

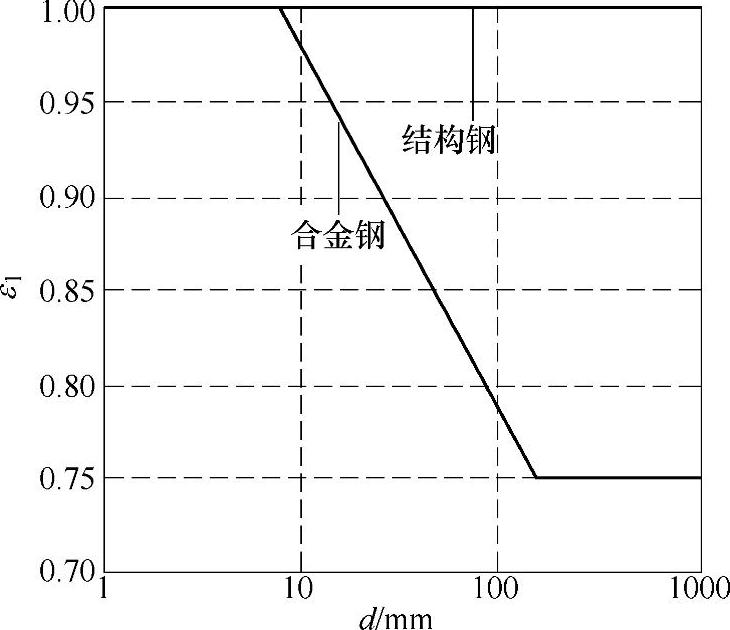
图8-6 技术尺寸系数ε₁

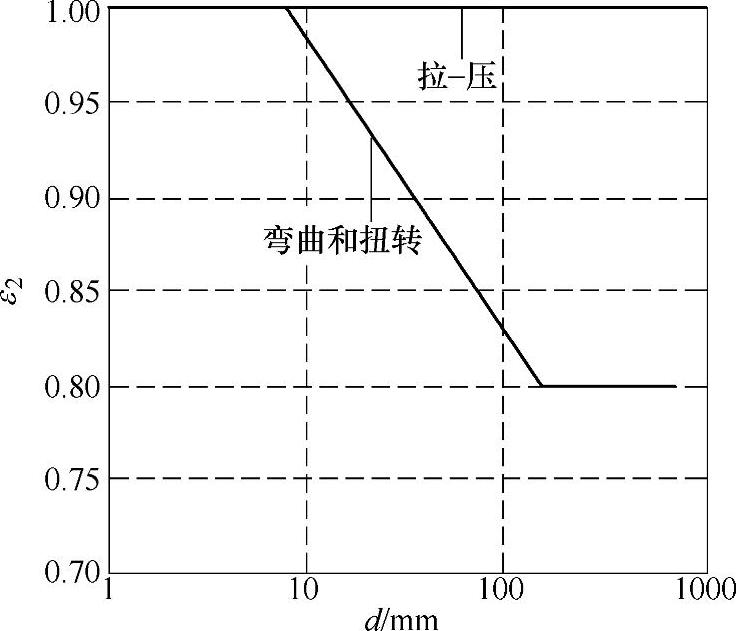
图8-7 几何尺寸系数ε₂

（3）表面质量的影响

疲劳裂纹常起源于不平整的表面或者细小的表面裂纹。试样的表面应该是抛光表面，表面粗糙度R_a=0.05～0.1μm，精机械加工的表面粗糙度R_a=0.4～16μm。表面质量的影响可用表面影响系数β来考虑（见图8-8），图中，R_a为表面粗糙度，σ_b为抗拉强度。

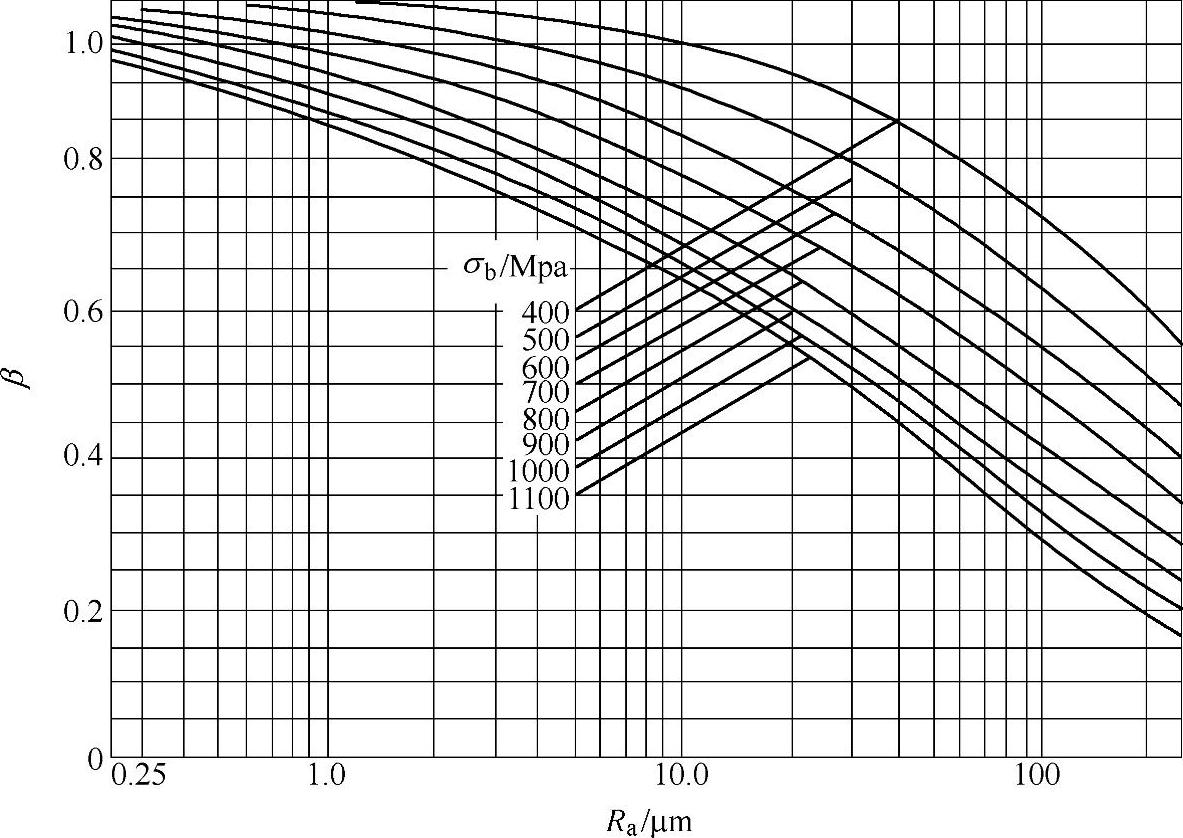
图8-8 表面质量系数β

（4）应力集中的影响

应力集中发生在几何形状发生变化的区域如轴肩、键槽等部位，也可以出现在锁紧盘连接及轴承过盈配合处。

常见的应力集中部位是轴肩等轴截面尺寸发生突变的部位，轴承附近常见结构如图8-9所示。图8-9中几何尺寸的数据见表8-1。

图8-9所示应力集中的影响可用有效应力集中系数（疲劳缺口系数）K_f来表示。有效应力集中系数主要取决于理论应力集中系数α，还与材料性质、缺口型式、缺口半径及深度有关。例如图8-10为阶梯轴弯曲的理论应力集中系数α，图中D为主轴轴肩处大径；d为主轴轴肩处小径；h为轴肩高度，h=（D-d）/2；r_c为过渡圆角半径。更多缺口型式的理论应力集中系数α参见《机械设计手册》（参考文献[7]，后同）。

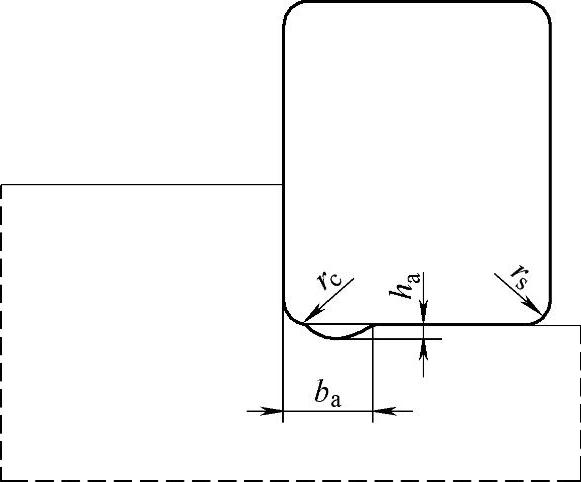
图8-9 轴承附近的主轴结构

表8-1 几何尺寸的数据

由缺口敏感因子q和理论应力集中系数α可以得出有效应力集中系数K_f，即

K_f=1+q（α-1） （8-6）

式（8-6）中，缺口敏感因子

式中 r_c——缺口半径；

A——Neuber系数（见图8-11），图8-11中σ_b为材料的抗拉强度。

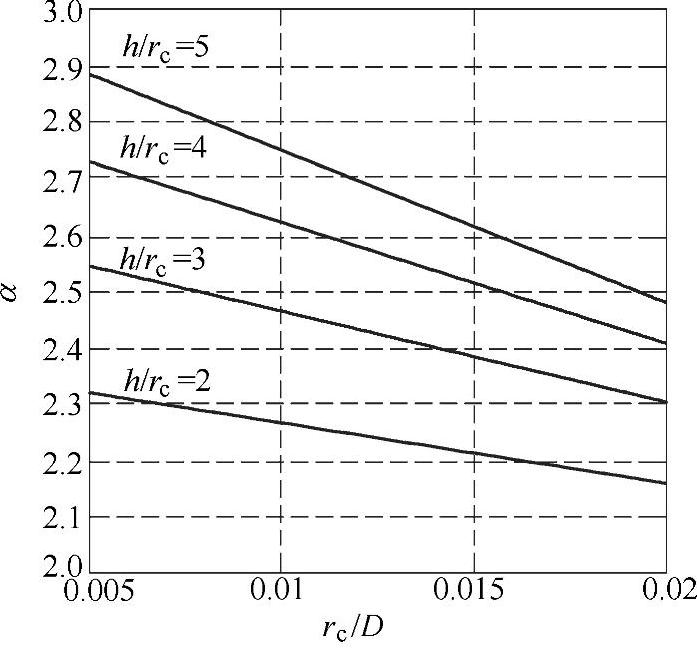
图8-10 理论应力集中系数α

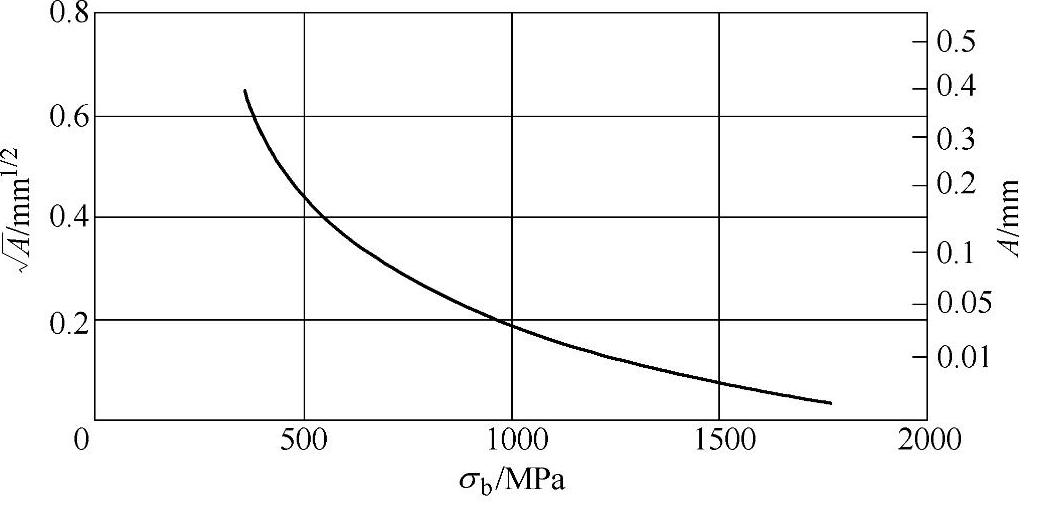
图8-11 Neuber系数

由于轴承紧配合造成的应力集中，可以采用应力集中系数K_f=1.1～1.2。

对于胀套联轴器连接，连接处的应力集中系数采用K_f=1.7～2.0。

（5）材料的S-N曲线 当缺少实际材料可靠的疲劳性能的试验数据时，可采用人为构造的S-N曲线。人为构造的S-N曲线有多种方法。推荐采用德国劳氏船级社的标准《Guideline for the Certification of Wind Turbines Edition 2003》规范中给定的方法对轮毂的疲劳S-N性能曲线进行拟合。

以下介绍适用于材料为低碳钢或合金钢的小尺寸7～10mm的抛光试件人为构造的S-N曲线的方法。它基于材料的静强度数据结合在旋转及扭转条件下（也可能是拉压）的疲劳极限σ_r。如果对实际材料没有σ_r，对拉压情况可以采用下面基于50％失效可能性的S-N曲线估算的疲劳极限：

σ_r50％=0.436σ_s+77

式中 σ_r50％——基于50％失效可能性的疲劳极限，单位为MPa；

σ_s——材料的屈服强度极限，单位为MPa。

为了得到2.3％失效概率下的疲劳极限，可按下式计算：

σ_r2.3％=σ_r50％-2s

式中 s——标准偏差，对低碳钢和低合金钢，s可取为σ_r50％的6％。

（6）疲劳强度校核 如果以lgS-lgN作为坐标轴，S-N曲线可认为从（10，σ_b）到（10⁶，σ_r）线性减小。当N＞10⁶时，曲线可视作水平线S=σ_r。

主轴各危险截面的疲劳强度可按下式校核：

式中 γ_f——载荷安全系数；

γ_m——材料安全系数。

安全系数γ_f、γ_m的数值见本书第三章。

式（8-8）、（8-9）中的K_f要分别用弯曲和扭转工况下的有效应力集中系数。

6.极限强度

除了前述强度校核之外，对高强度极限的主轴材料，还应该考虑极限载荷工况同时可能兼有应力集中影响下的极限强度。应力集中对极限强度的影响可用系数γ_e来考虑

式中 σ_b——材料的抗拉强度，单位为MPa；

α——应力集中系数，查图8-10。

则极限强度校核式为

式中 σ_s——材料的屈服极限，单位为MPa；

γ_f——载荷安全系数；

γ_m——材料安全系数。