叶片强度与稳定性校核分析

为了保证风力发电机组的可靠运行和使用寿命，需要对叶片总体结构性能进行分析，包括对其在极限载荷条件下的强度、变形、稳定性以及疲劳强度等进行校核计算。图6-21所示为叶片总体结构基本分析内容及其步骤。

1.极限强度分析

在校核叶片极限强度时，可将叶片视为一端固定的悬臂梁。将其截面简化为图6-22所示的三个基本的几何形状，图中的矩形代表主梁，半椭圆形和三角形分别代表翼型的前缘和后缘。

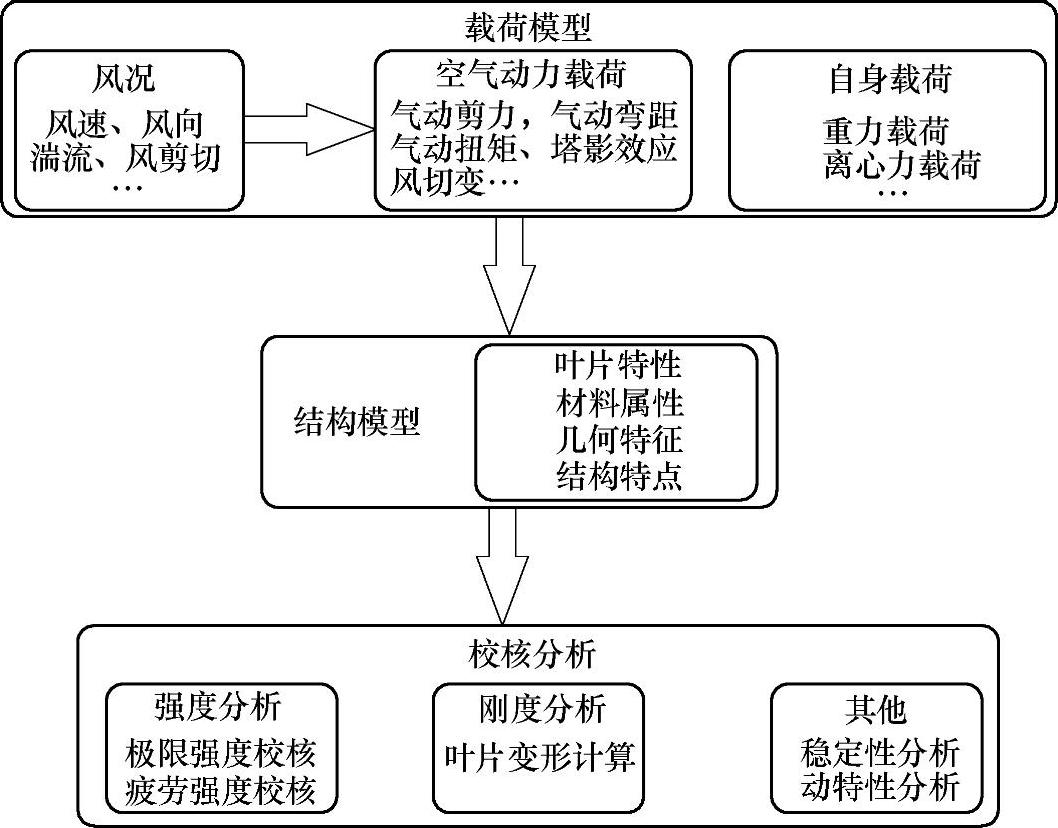
图6-21 叶片总体校核

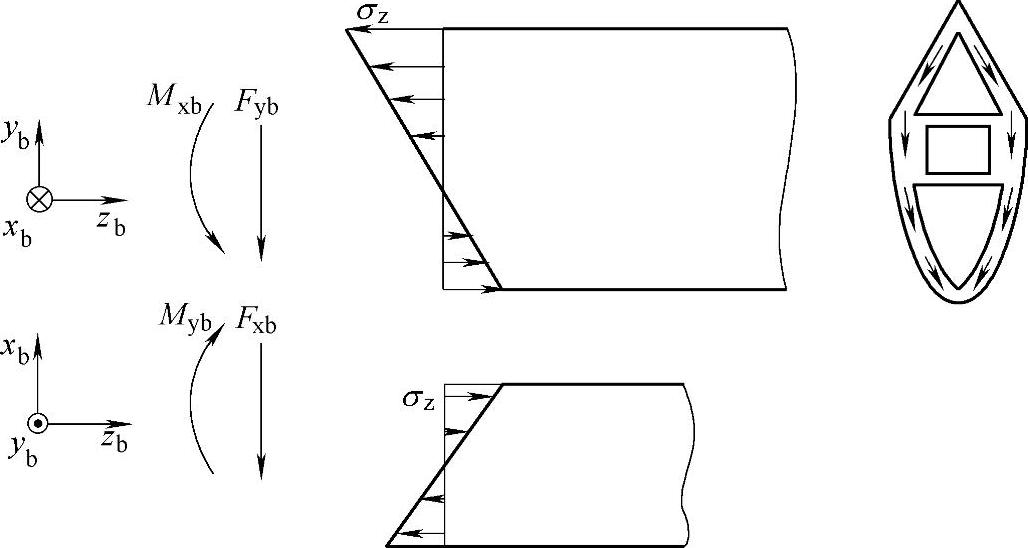
图6-22 叶片主梁所受应力

为了简化计算，假设横截面对称于y轴，且从叶根到叶尖采用等强度截面设计。将作用在叶片上的载荷转换为截面坐标系上的等效载荷，则截面的应力公式为

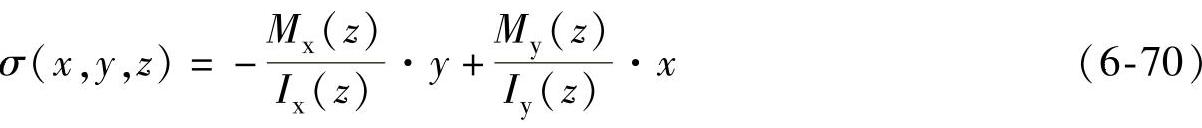
式中 σ（x，y，z）——截面的应力，单位为Pa；

M_x（z）、M_y（z）——相对于x、y轴的弯曲力矩，单位为N·m；

I_x（z）、I_y（z）——相对于x、y轴的惯性矩，单位为m⁴。

由式（6-70）可求出叶片危险截面的最大应力，并根据对强度条件进行应力校核，从而判断叶片是否具有足够的静态强度。

强度条件为

γσ_max＜[σ] （6-71）

式中 [σ]——材料的许用应力；

σ_max——实际计算出的最大应力；

γ——为安全系数。

2.稳定性分析

大型风轮叶片为空腔结构形式，在弯曲气动载荷作用下，叶片局部受压区域可能发生突然损坏，成为失稳现象。由于叶片后缘空腔较宽，更容易发生失稳。因此，需要对叶片结构进行稳定性分析。

稳定性分析一般采用近似方法。对于O形、D形等主梁结构或空腹壳体，可近似应用曲板的轴压稳定公式：

式中 E——弹性模量；

R——剖面的曲率半径；

b——剖面宽度；

δ——为剖面壁厚。

对于后缘空腔采用泡沫夹层结构，应用相应的失稳临界应力方程：

式中 E_f——面板模量；

D——弯曲刚度；

H——拉伸刚度；(www.xing528.com)

k——由板的长宽比和弯曲、剪切刚度决定的常数。

临界应力计算受计算方法、材料性能、制造工艺等因素影响，与实际临界应力值有比较大的误差，故需要有较大的安全系数。

通过稳定性分析，得到每一剖面的临界压应力。设计要求叶片的最大压应力低于临界压应力。初步设计计算可满足工程要求，但优化设计应采用有限元方法。

3.变形分析

由于载荷作用，叶片会发生弯曲和扭转变形，叶片越长变形越显著。运行于极端状态的风力发电机组，应避免叶片与塔架之间产生碰撞，相关的风电技术标准对此也有明确的规定。GL准则规定，在极限载荷条件下，叶片最大变形不超过叶尖与塔架间隙的50％。

叶片变形计算可采用如下办法计算。

（1）叶尖变形

在外力作用下，叶片微段dr的变形如图6-23所示。

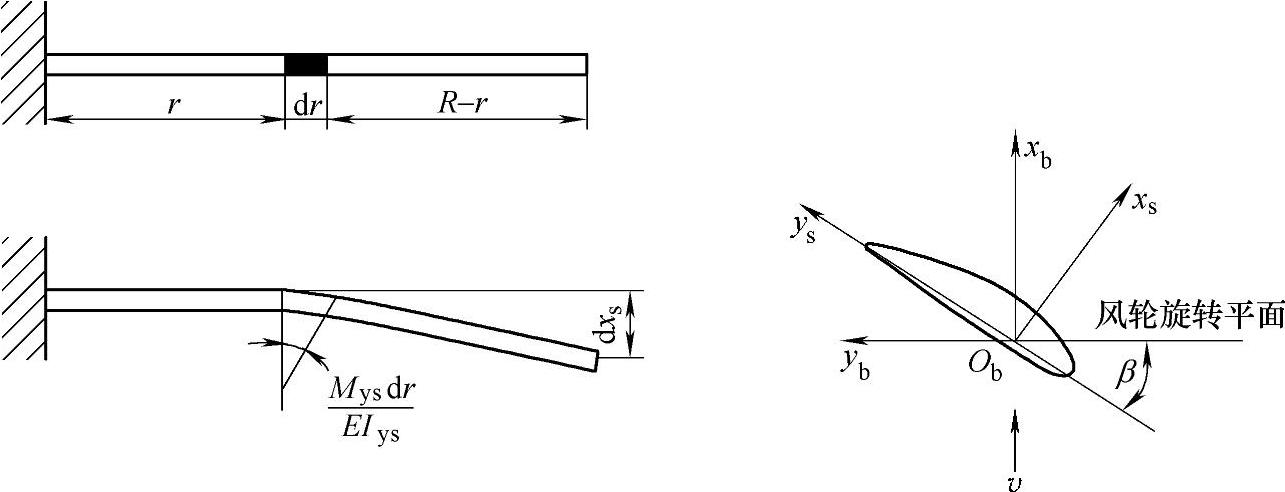
图6-23 叶片微段dr的变形

假定只有dr段是柔性的，其他部分为刚性的，则由于dr段变形引起的叶尖变形可表示为

式中 M_ys、M_xs——dr段相对y_s、x_s轴的弯矩。且有：

M_xs=M_xbcosβ-M_ybsinβ

M_ys=M_ybcosβ+M_xbsinβ

式中 β——叶素桨距角。

由于I_xs的数值较大，通常可以不计叶片在y_s方向的变形。将式（6-74）表述的变形转换到叶片坐标系下，则在x_b、y_b方向的变形依次为

dx_b=dx_scosβ （6-76）

dy_b=-dx_ssinβ （6-77）

沿叶片展向对式（6-76）、式（6-77）积分，可得到叶尖的位移为

叶尖的总变形：

叶片上任意位置的变形，可将上述积分上限R改为该位置的R_i值即可。

（2）叶素桨距角的变化

由z_s轴力矩M_zs引起的叶素桨距角的变化可采用闭口薄壁杆件的扭转公式计算。叶片的扭转角为

式中 M_zs——叶片承受的扭矩，单位为N·m；

G——剪切弹性模量，单位为Pa；

I_zs——截面极惯性矩，单位为m⁴。